Установите соответствие между видом и классом эконометрических уравнений.
(1) 
(2) 
(3) 
система независимых уравнений 1
система рекурсивных уравнений 2
система одновременных уравнений 3
система нормальных уравнений
4. Установите соответствие между видом и классом системы эконометрических уравнений:
(1) 
(2) 
система одновременных уравнений с лаговыми переменными 1
система независимых уравнений 2
система одновременных уравнений без лаговых переменных
5. Установите соответствие между классом и видом системы эконометрических уравнений:
(1) система одновременных уравнений
(2) система рекурсивных уравнений
(3) система независимых уравнений
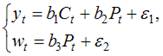
Тема 23: Идентификация систем эконометрических уравнений
Модель мультипликатора-акселератора Кейнса
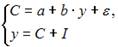
где C – личное потребление в постоянных ценах,
y – национальный доход в постоянных ценах,
I – инвестиции в постоянных ценах,
– случайная составляющая,
Установите соответствие:
(1) эндогенная переменная
(2) экзогенные переменная.
y – национальный доход в постоянных ценах
I – инвестиции в постоянных ценах
– случайная составляющая
Решение:
В модели мультипликатора-акселератора Кейнса эндогенными переменные являются переменные C (личное потребление в постоянных ценах) и y (национальный доход в постоянных ценах). А экзогенными переменными является только переменная I (инвестиции в постоянных ценах). И является случайной составляющей.
|
|
|
2. Дана структурная форма модели системы одновременных уравнений:
Установите соответствие между обозначением и его наименованием:
(1) 
(2) 
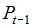
(3) 
ошибка модели
лаговая переменная
эндогенная переменная
структурный коэффициент
Установите соответствие между структурной формой модели и приведенной формой модели
(1) 
где C – личное потребление в постоянных ценах,
y – национальный доход в постоянных ценах,
I – инвестиции в постоянных ценах
(2) 
где R – процентная ставка,
Y – ВВП,
M – денежная масса,
I – инвестиции
где C – личное потребление в постоянных ценах,
y – национальный доход в постоянных ценах,
I – инвестиции в постоянных ценах 
где R – процентная ставка,
Y – ВВП,
M – денежная масса,
I – инвестиции 
где C – личное потребление в постоянных ценах,
y – национальный доход в постоянных ценах,
I – инвестиции в постоянных ценах 
Установите соответствие между структурной формой модели и приведенной формой модели
(1)
где C – личное потребление в постоянных ценах,
y – национальный доход в постоянных ценах,
I – инвестиции в постоянных ценах
(2) 
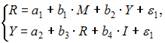
где R – процентная ставка,
Y – ВВП,
M – денежная масса,
I – инвестиции
где C – личное потребление в постоянных ценах,
|
|
|
y – национальный доход в постоянных ценах,
I – инвестиции в постоянных ценах
где R – процентная ставка,
Y – ВВП,
M – денежная масса,
I – инвестиции 
где C – личное потребление в постоянных ценах,
y – национальный доход в постоянных ценах,
I – инвестиции в постоянных ценах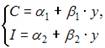 
Тема 24: Методы оценки параметров систем одновременных уравнений: косвенный метод наименьших квадратов (КМНК) и двухшаговый метод наименьших квадратов (ДМНК)
1. Если записать типы эконометрических моделей в следующем порядке:
1) точно идентифицируемая система одновременных уравнений,
2) сверхидентифицируемая система одновременных уравнений,
3) уравнение множественной регрессии,
4) уравнение множественной регрессии при автокорреляции остатков,
то методы, применяемые для нахождения параметров соответствующих типов эконометрических моделей, будут расположены в следующем порядке
косвенный метод наименьших квадратов
двухшаговый метод наименьших квадратов
метод наименьших квадратов
обобщенный метод наименьших квадратов
Поэтому порядок методов, соответствующих типам эконометрических моделей будет следующий:
– косвенный метод наименьших квадратов;
|
|
|
– двухшаговый метод наименьших квадратов;
– метод наименьших квадратов;
– обобщенный метод наименьших квадратов.
Система независимых эконометрических уравнений может быть идентифицирована с помощью обычного метода наименьших квадратов. Определите последовательность этапов алгоритма оценки параметров для такой модели.
оценка возможности идентификации модели как системы независимых уравнений
разделение системы независимых уравнений на отдельные уравнения регрессии
построение общего вида системы нормальных уравнений для каждого уравнения системы и расчет необходимых значений сумм
решение системы нормальных уравнений для каждого уравнения системы
подстановка найденных значений оценок параметров в уравнения системы
Решение:
1) разложение системы независимых уравнений на отдельные (изолированные) уравнения регрессии, число которых определяется количеством эндогенных переменных модели;
2) построение системы нормальных уравнений для каждого отдельного (изолированного) уравнения; 3) расчет оценок параметров каждого отдельного (изолированного) уравнения;
4) запись системы независимых уравнений с найденными значениями оценок параметров.
|
|
|
3. Дана система одновременных эконометрических уравнений:
Система является точно идентифицируемой. Определите последовательность этапов алгоритма оценки ее параметров.
преобразование структурной формы модели в приведенную форму вида
оценивание параметров приведенной формы модели (приведенных коэффициентов)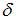 
для каждого уравнения приведенной формы модели обычным МНК оцениваются
трансформация коэффициентов приведенной формы модели в параметры структурной формы модели 
и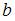 
подстановка найденных значений коэффициентов в структурную форму системы эконометрических уравнений
Решение:
1) структурная форма модели преобразовывается в приведенную форму модели; так как в системе 4 экзогенных переменных – (х1, х2, х3 и х4),то у правой части приведенной формы модели записывается сумма четырех произведений соответствующих коэффициентов приведенной формы и экзогенных переменных; для данной системы приведенная форма будет иметь вид
2) для каждого уравнения приведенной формы модели обычным МНК оцениваются параметры приведенной формы модели – приведенные коэффициенты ;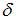
3) коэффициенты приведенной формы модели трансформируются в параметры структурной формы модели и ;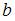
4) найденные значения коэффициентов подставляются в структурную форму системы эконометрических уравнений.
5. При проверке счетного правила выяснилось, что для всех уравнений системы одновременных уравнений выполняется необходимое условие идентификации и все уравнения по счетному правилу точно идентифицируемы. Чтобы получить структурные коэффициенты системы, действия нужно выполнить в следующем порядке:
1.для каждого уравнения проверить условие неравенства нулю определителя матрицы коэффициентов, присутствующих в других уравнениях, но отсутствующих в данном уравнении
2.преобразовать структурную форму модели в приведенную форму модели
3.для каждого уравнения приведенной формы модели обычным методом наименьших квадратов оценить приведенные коэффициенты
4.коэффициенты приведенной формы модели преобразовать в параметры структурной модели
6. При проверке счетного правила выяснилось, что для всех уравнений системы одновременных уравнений выполняется необходимое условие идентификации и все уравнения по счетному правилу сверхидентифицируемы. Чтобы получить структурные коэффициенты системы, действия нужно выполнить в следующем порядке:
для каждого уравнения проверить условие неравенства нулю определителя матрицы коэффициентов, присутствующих в других уравнениях, но отсутствующих в данном уравнении
преобразовать структурную форму модели в приведенную форму модели
для каждого уравнения приведенной формы модели обычным методом наименьших квадратов оценить приведенные коэффициенты
на основе коэффициентов приведенной формы модели получить теоретические значения эндогенных переменных, содержащихся в правой части сверхидентифицированных уравнений
5 применить обычный метод наименьших квадратов, подставив вместо фактических значений эндогенных переменных, стоящих в правой части уравнения, рассчитанные теоретические значения, и получить структурные коэффициенты модели
Кейс 1 подзадача 1
1. По 72 банкам построено уравнение зависимости размеров кредитов, выданных предприятиям и организациям, в млн. руб. (y) от собственного капитала, млн руб. (x): y = 710,967 + 3,057 ∙ x . Исходные данные упорядочены по убыванию величины собственного капитала. По величинам остатков рассчитан коэффициент автокорреляции первого порядка, равный -0,45539. На рисунке представлен график остатков.
Проанализировав график остатков, можно сделать вывод о том, что …
нарушена предпосылка о гомоскедастичности остатков
Дата добавления: 2018-02-15; просмотров: 2159; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!