Классификация, принцип действия, особенности и область применения теплообменников различного типа. Основы конструктивного теплового расчета теплообменных аппаратов.

Типы теплообменных аппаратов

Теплообменным аппаратом называют всякое устройство, в котором одна жидкость — горячая среда, передает теплоту другой жидкости — холодной среде. В качестве теплоносителей в тепловых аппаратах используются разнообразные капельные и упругие жидкости в самом широком диапазоне давлений и температур. По принципу работы аппараты делят на регенеративные, смесительные и рекуперативные.

В регенеративных аппаратах горячий теплоноситель отдает свою теплоту аккумулирующему устройству, которое в свою очередь периодически отдает теп лоту второй жидкости — холодному теплоносителю, т. е. одна и та же поверхность нагрева омывается то горячей, то холодной жидкостью.

В смесительных аппаратах передача теплоты от горячей к холодной жидкости происходит при непосредственном смешении обеих жидкостей, например смешивающие конденсаторы.

Особенно широкое развитие во всех областях техники получили рекуперативные аппараты, в которых теплота от горячей к холодной жидкости передается через разделительную стенку. Только такие аппараты будут рассмотрены в дальнейшем.

Теплообменные аппараты могут иметь самые разнообразные назначения — паровые котлы, конденсаторы, пароперегреватели, приборы центрального отопления и т. д. Теплообменные аппараты в большинстве случаев значительно отличаются друг от друга как по своим формам и размерам, так и по применяемым в них рабочим телам. Несмотря на большое разнообразие теплообменных аппаратов, основные положения теплового расчета для них остаются общими.

В теплообменных аппаратах движение жидкости осуществляется по трем основным схемам.

Если направление движения горячего и холодного теплоносителей совпадают, то такое движение называется прямотоком (рис. 30-1, а). Если направление движения горячего теплоносителя противоположно движению холодного теплоносителя, то такое движение называется противотоком (рис. 30-1, б). Если же горячий теплоноситель движется перпендикулярно движению холодного теплоносителя, то такое движение называется перекрестным током (рис. 30-1, в). Кроме этих основных схем движения жидкостей, в теп-лообменных аппаратах применяют более сложные схемы движения, включающие все три основные схемы.

Основные положения теплового расчета

При проектировании новых аппаратов целью теплового расчета является определение поверхности теплообмена, а если последняя известна, то целью расчета является определение конечных температур рабочих жидкостей. Основными расчетными уравнениями теплообмена при стационарном режиме являются уравнение теплопередачи и уравнение теплового баланса.

Уравнение теплопередачи (24-6) 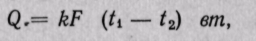где Q — тепловой поток, вm; k — средний коэффициент теплопередачи, вт/м²-град; F — поверхность теплообмена в аппарате, м²; t₁и t₂ — соответственно температуры горячего и холодного теплоносителей.

Уравнение теплового баланса при условии отсутствия тепловых потерь и фазовых переходов:

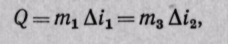или 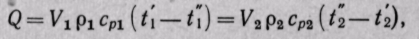где V₁ρ₁ и V₂ρ₂— массовые расходы теплоносителей, кг/сек;

c_p₁ и С_Р2—средние массовые теплоемкости жидкостей в интервале температур от f до t";

t'₁и t'₂—температуры жидкостей при входе в аппарат; t"₁ и t''₂—температуры жидкостей при выходе из аппарата. Величину произведения называют водяным, или условным, эквивалентом.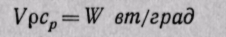

С учетом последнего уравнение теплового баланса может быть представлено в следующем виде: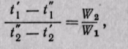

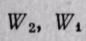- условные эквиваленты горячей и холодной жидкостей.

В тепловом аппарате температуры горячей и холодной жидкостей изменяются обратно пропорционально их условным эквивалентам. Это соотношение сохраняется и для каждого элемента поверхности аппарата:

где 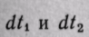- изменения температуры горячего и холодного теплоносителей на элементе поверхности аппарата.

Соотношение между величинами условных эквивалентов горячей и холодной среды определяет наклон температурных кривых на графиках изменения температур. Например, если W₁ = 2W₂, то изменение температуры холодного теплоносителя будет вдвое больше изменения температуры горячего теплоносителя.

При выводе основного уравнения теплопередачи (24-6) принималось, что температуры горячей и холодной среды в теплообменном аппарате не изменяются. В действительности температуры рабочих жидкостей при прохождении через аппарат изменяются, причем на изменение температур большое влияние оказывают схема движения жидкостей и величины условных эквивалентов.

Если по оси абсцисс откладывать значения поверхности аппарата, а по оси ординат — значения температур в различных точках поверхности, то для аппаратов с прямотоком можно дать температурные графики, представленные на рис. 30-2.

Для аппаратов с противотоком (рис. 30-3) верхние кривые показывают изменение температуры горячего теплоносителя, нижние — холодного.

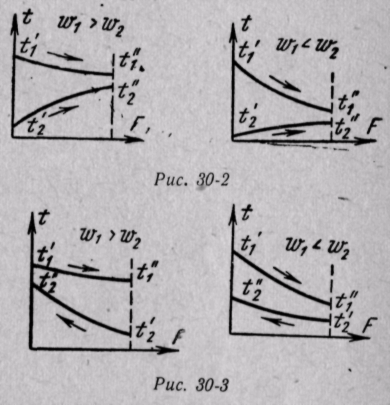Как видно из рис. 30-2, при прямотоке конечная температура холодного теплоносителя всегда ниже конечной температуры горячего теплоносителя. При противотоке (см. рис. 30-3) конечная температура холодной жидкости может быть значительно выше конечной температуры горячей жидкости. Следовательно, в аппаратах с противотоком можно нагреть холодную среду, при одинаковых начальных условиях, до более высокой температуры, чем в аппаратах с прямотоком. Кроме того, как видно из рисунков, наряду с

изменениями температур изменяется также и разность температур между рабочими жидкостями, или температурный напор ∆t.

Величины ∆t и k можно принять постоянными только в пределах элементарной поверхности теплообмена dF. Поэтому уравнение теплопередачи для элемента поверхности теплообмена dF справедливо лишь в дифференциальной форме:

Тепловой поток, переданный через всю поверхность F при постоянном среднем коэффициенте теплопередачи k, определяется интегрированием уравнения (30-3): 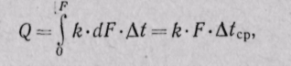(30-4)

где ∆t_ср — средний логарифмический температурный напор по

всей поверхности нагрева.

Для случаев, когда коэффициент теплопередачи на отдельных участках поверхности теплообмена значительно изменяется, его усредняют:

Тогда при k_fp — const уравнение (30-4) примет вид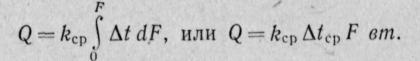

Дата добавления: 2018-02-15; просмотров: 808; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 16 17 18 19 202122 23 24 25 Следующая ⇒

Мы поможем в написании ваших работ!