Теплопроводность через многослойную плоскую стенку

В тепловых аппаратах часто встречаются стенки, состоящие из нескольких плоских слоев различных материалов. Выведем урав­нение для этого случая, полагая, что все слои плотно прилегают друг к другу.

Расчетную формулу теплопроводности сложной стенки при ста­ционарном состоянии можно вывести из уравнения теплопроводно­сти для отдельных слоев, считая, что тепловой поток, проходящий через любую изотермическую поверхность неоднородной стенки, один и тот же.

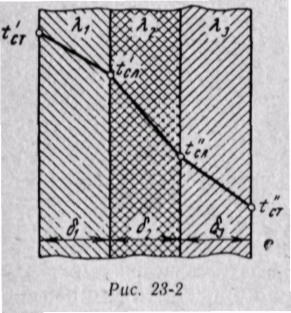
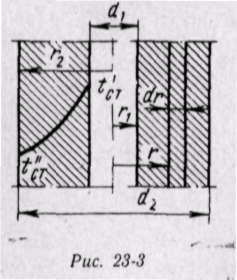
Для решения этой задачи рассмотрим трехслойную стенку, в которой толщина отдельных слоев равна δ₁, δ₂, δ₃, а их коэф­фициенты теплопроводности соответственно λ_1, λ₂, λ₃ (рис. 23-2). Температуры наружных поверхностей t_ст и ''t_ст; температуры между слоями t'_сл и t''_сл.

Теплопроводность через однослойную цилиндрическую стенку

Внешняя и внутренняя поверхности прямой цилиндрической трубы поддерживаются при постоянных температурах t'_ст и t''_ст. Изотермические поверхности будут цилиндрическими поверхностя­ми, имеющими общую ось с трубой. Температура будет меняться только в направлении радиуса, благодаря этому и поток тепла будет тоже радиальным. Труба имеет бесконечную длину. Температурное поле в этом случае будет одномерным

где r — текущая цилиндрическая координата.

В случае неравномерного распределения температур на поверх­ностях трубы температурное поле не будет одномерным и последнее уравнение не будет действительным.

На рис. 23-3 изображена труба, в которой тепловой поток направ­лен по радиальным направлениям. Возьмем участок трубы длиной l.

Тепловой поток для каждого слоя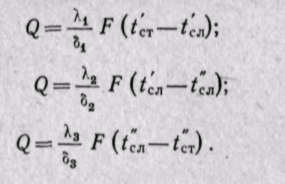

Решая эти уравнения относительно разности температур и скла­дывая, получаем

откуда

 

(23-8)

или для любого числа слоев

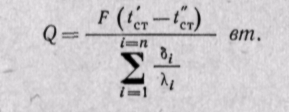 (23-9)

Отношение называют термическим сопротивлением слоя, а

величину —полным термическим сопротивлением многослойной плоской стенки.

Иногда многослойную плоскую стенку рассчитывают как одно­родную, вводя в уравнение (23-9) эквивалентный коэффициент теп­лопроводности λ_эк:

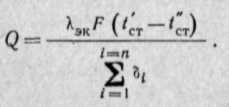 (23-10)

Сравнивая уравнения (23-9) и (23-10), получаем

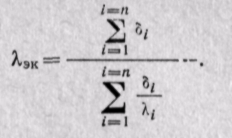 (23-11)

Эквивалентный коэффициент теплопроводности многослойной стенки равен коэффициенту теплопроводности однородной стенки той же толщины, с теми же температурами поверхностей и про­пускающей тот же тепловой поток.

Величина λ_эк зависит от термических сопротивлений и толщин отдельных слоев.

Температуры в ◦С между отдельными слоями сложной стенки будут равны

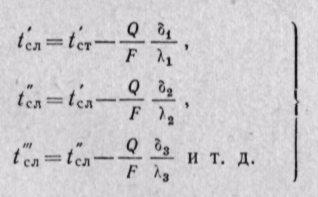 (23-12)

Температура в каждом слое стенки при постоянном коэффициен­те теплопроводности изменяется по линейному закону, а для много­слойной плоской стенки температурный график представляет собой ломаную линию.

Поверхность F на расстоянии г от оси будет равна 2лrl. Темпера­тура внутренней поверхности равна t'_ст, наружной — t''_ст. Через поверхности проходит один и тот же тепловой поток.

Выделим внутри стенки кольцевой слой радиусом г и толщиной dr. Тогда можно принять поверхности, через которые проходит тепловой поток, одинаковыми и рассматривать этот элементарный слой как плоскую стенку. Разность температур между поверхностя­ми будет также бесконечно малой и рав­ной dt. По закону Фурье или для кольцевого слоя

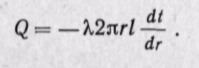
Разделяя переменные, получаем

 

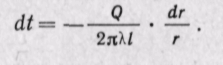
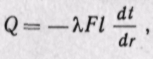                                                                                                            (а)

Интегрируя уравнение (а) в пределах от t'_ст До t''_ст и от r₁ до r₂ и при К — const, получаем

откуда 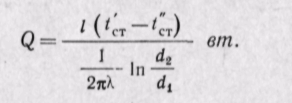(23-13)

Как видно из уравнения, распределение температур в стенке цилиндрической трубы представляет собой логарифмическую кри­вую. Тепловой поток, проходящий через цилиндрическую стенку, определяется заданными граничными условиями и зависит от отно­шения наружного диаметра к внутреннему.

Тепловой поток может быть отнесен к единице длины трубы и к 1 м² внутренней или внешней поверхности. Тогда расчетные фор­мулы принимают вид

 

---

Дата добавления: 2018-02-15; просмотров: 1427; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!