Рассмотрение энергетической и геометрической интерпретации уравнения Бернулли
С энергетической точки зрения уравнение Бернулли выражает закон сохранения энергии и представляет удельную энергию, отнесенную к единице веса жидкости и подсчитанную относительно произвольно выбранной горизонтальной плоскости. Такая удельная энергия потока состоит из удельной потенциальной энергии 
где z – энергия положения, 
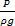- энергия давления, и удельной кинетической энергии потока 
. С теоретической точки зрения потери энергии 
на преодоление сопротивления безвозвратно теряются для потока, т.е. часть механической энергии превращается в тепловую.
С геометрической точки зрения в уравнение Бернулли входят следующие линейные величины:
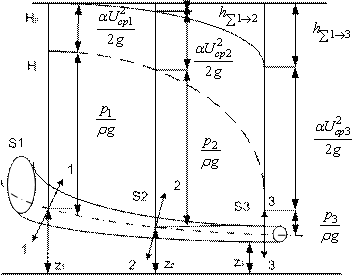
Рис. 5.2
z – геометрическая высота положения (геометрический напор);
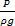или 
пьезометрическая высота, отвечающая гидродинамическому давлению р;
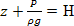в каждом сечении называется пьезометрическим (при р=ризб) или гидростатическим напором;
- скоростной напор;
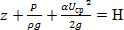0 – гидродинамический или полный напор;
- потеря напора на преодолении сопротивлений.
Геометрическое место точек верхних концов отрезка суммы называется пьезометрической линией Н (на рис.5.2 показана штриховкой). Изменение пьезометрической линии на единицу длинны поток называется пьезометрическим уклоном ip.
Геометрическое место точек верхних концов отрезков суммы 
называется напорной линией или линией удельной энергии Но (на рис.5.2 показана сплошной линией), которая для потока идеальной жидкости т.е. без потерь энергии, будет горизонтальной. При движении вязкой жидкости изменение напорной линии на единицу длинны потока называется гидравлическим уклоном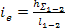 
.
|
|
|
Виды гидравлических сопротивлений (на трение, местные сопротивления, теоретическое обоснование расчета).
Потерянные на сопротивление напоры в зависимости от характера препятствий, делят на две большие группы:
- потери напора по длине потока, или потери напора на трение;
-потери напора за счет местных сопротивлений.
Потери напора на трение, или гидравлическое трение, обуславливаются вязкостью, реальных жидкостей и газов, возникающей при их движении, и являются результатом обмена количеством движения между молекулами (при ламинарном течении), а также и между отдельными частицами (при турбулентном движении) соседних слоев жидкости (газа), движущихся с различными скоростями.
Для преодоления сопротивления трения и поддержания равномерного поступательного движения жидкости необходимо, чтобы на жидкость действовала сила направленная в сторону её движения и равная силе сопротивления, т.е. на преодоление сопротивления трения нужно затрачивать энергию. Поэтому необходимую для преодоления сил сопротивления энергию или напор называют потерянной энергией или потерями напора.
|
|
|
При движении жидкости между нею и стенками трубы возникают дополнительные силы сопротивления, в результате чего частицы жидкости, прилегающие к поверхности трубы, тормозятся. Это торможение вследствие вязкости жидкости передается следующим слоям, причем скорость движения частиц по мере удаления от оси трубы постепенно уменьшается. Равнодействующая сил, сопротивления, Т, направлена в сторону противоположную движению, и параллельна направлению движения. Это и есть сила гидравлического трения (сопротивление гидравлического трения).
Потери напора за счет местных сопротивлений, возникают при местном нарушении нормального течения. За местные сопротивления принимают вентиль, кран, обратный клапан, внезапное расширение, сужение или поворот трубы, разветвление потока, протекание жидкости через отверстия, решетки, дроссельные устройства, обтекание различных препятствий и т.п. Эти явления усиливают обмен количеством движения между частицами движущейся .жидкости (т.е. трение), повышая потери энергии.
|
|
|
Таким образом, потери напора при движении жидкости складываются из потерь напора на трение и потерь напора на местные сопротивления, т.е.
Потери напора на трение зависят от следующих факторов: диаметра трубы d и её длины L, физических свойств жидкости (плотности r и вязкости m), средней скорости движения жидкости в трубе V, средней высоты выступов шероховатости К на стенках трубы.
Формула для определения потерь на трение была получена в XIX в. эмпирическим путем и называется формулой Дарси - Вейсбаха: 
где l - коэффициент гидравлического трения, зависящий как от степени шероховатости стенок, так и от режима движения.
Потери напора на местное сопротивление находят по формуле Вейсбаха: 
где V - коэффициент местных потерь; V - скорость потока после прохода через местное сопротивление.
Местные гидравлические сопротивления вызываются фасонными частями, арматурой и другим оборудованием трубопроводных сетей, которые изменяют величину или направление скорости движения жидкости на отдельных участках трубопровода (при расширении или сужении потока, в результате его поворота, при протекании потока, через диафрагмы, задвижки и т.д.), что всегда связано с появлением дополнительных потерь напора.
|
|
|
Потери напора, возникающие при преодолении какого-либо местного сопротивления, принято оценивать в долях скоростного напора, соответствующего скорости непосредственно за рассматриваемым местным сопротивлением, т.е. определять их по формуле Вейсбаха.
Коэффициенты разных местных сопротивлений находят, как правило, опытным путем. Таблицы значений этих коэффициентов (или формулы для них) содержатся в инженерных справочниках и руководствах по гидравлике. Для некоторых практически важных случаев значения коэффициентов местных сопротивлений удалось получить, также и теоретическим путем.
Иногда местные потери напора выражают в виде эквивалентной длины Lэ прямого участка трубопровода, сопротивление трения которого по величине равно рассматриваемым местным потерям напора т.е. из условия 
или 
Таким образом, эквивалентная длина учитывает влияние коэффициента гидравлического трения трубопровода, где имеется местное сопротивление, на величину местных потерь напора. В соответствии с этой формулой V возрастает прямо пропорционально l, а следовательно, уменьшается с повышением числа Рейнольдса и снижением относительной шероховатости. При заданной геометрии местного сопротивления V является функцией коэффициента гидравлического трения l.
Основные виды местных потерь напора можно условно разделить на следующие группы:
- потери, связанные с изменением живого сечения потока ( или, что то же, его средней скорости), куда относятся случаи расширения и сужения потока (внезапного или постепенного);
-потери, вызванные изменением направления потока, его поворотом (движение жидкости в коленах, угольниках, отводах на трубопроводах);
-потери, связанные с протеканием жидкости через арматуру различного типа (вентили, краны, обратные клапаны, сетки, отборы, дроссель-клапаны и т.д.);
-потери, возникшие вследствие отделения одной части потока от другой или слияния двух потоков в один общий (движение жидкости в тройниках, крестовинах и отверстиях в боковых стенках трубопроводов при наличии транзитного расхода).
На участках многих местных сопротивлений скорости потока резко возрастают, в результате чего давление в нем уменьшается. Если давление становится ниже давления насыщенных паров жидкости, протекающей через местное сопротивление (или непосредственно за ним), возникает кавитация, неблагоприятно отражающаяся на работе оборудования и приводящая к вибрации, шумам и эрозионному разрушению материала. При наличии кавитации местные потери напора заметно возрастают. Кавитационные свойства местных сопротивлений оцениваются по критическому значению безразмерного числа – 
числа кавитации X, при котором в данном местном сопротивлении начинается кавитация:
P1 – давление перед местным сопротивлением; Pкр - минимальное давление, при котором возникает кавитация, V1 - средняя скорость перед местным сопротивлением.
Обычно кавитация возникает при минимальном давлении, равном давлению насыщенных паров, т.е. 
При достижении числом кавитации предельно допустимого (критического) значения Xкр в рассматриваемом местном сопротивлении начинается кавитация. Значения критического числа кавитации для разных местных сопротивлений определяются, как правило, экспериментально. Они связаны с коэффициентом местного сопротивления в бескавитационном режиме. В первом приближении для местных сопротивлений, вызванных изменением сечения потока, можно предложить зависимость: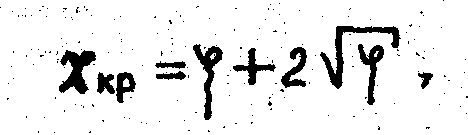 
где V - коэффициент местного сопротивления.
Если известно значение критического числа кавитации Xкр, то предельно допустимую скорость в трубопроводе перед местным сопротивлением определяют по формуле: 
Для скоростей, не превышающих Vпр коэффициенты местного сопротивления определяют без учета влияния кавитации.
Дата добавления: 2018-02-15; просмотров: 845; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!