Гидравлический расчет сложных трубопроводов.
Сложный трубопровод состоит из простых трубопроводов с последовательным и параллельным их соединением или с разветвлениями.
При расчетах сложных трубопроводов их разбивают на простые участки, участки с разветвлениями и параллельными трубопроводами и, идя от конечных точек сложного трубопровода к начальной его точке, т.е. против течения, последовательно производят расчеты по приведенным выше уравнениям.
Для сложных кольцевых трубопроводов (системы смежных замкнутых контуров с отборами жидкости в узловых точках или непрерывной раздачей ее на отдельных участках) используют два основных условия:
· баланс расходов, т.е. равенство притока и оттока жидкости для каждой узловой точки;
· баланс напоров, т.е. равенство нулю алгебраической суммы потерь напора для каждого контура при подсчете по направлению движения часовой стрелки. Потери напора считают положительными, если направление подсчета совпадает с направлением движения жидкости, и отрицательными, если направление подсчета противоположно направлению движения жидкости.
Сложный трубопровод в общем случае составлен из простых трубопроводов с последовательным и параллельным их соединением (рис. 6.6, а) или с разветвлениями (рис. 6.6, б).

Рис. 6.6. Схемы сложных трубопроводов
Рассмотрим разомкнутый сложный трубопровод (рис. 6.6, б). магистральный трубопровод разветвляется в точках А и С. Жидкость подается к точкам (сечениям) B, D и E с расходами Q B и QD и QE .
Пусть известны размеры магистралей и всех ветвей (простых трубопроводов), заданы все местные сопротивления, а также геометрические высоты конечных точек, отсчитываемые от плоскости M - N и избыточные давления в конечных точках PB и PD и PE.
Для этого случая возможны два вида задач:
Задача 1. Дан расход Q в основной магистрали MA. Необходимо определить расходы QB и QD и QE, а также потребный напор в точке М.
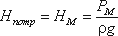
Задача 2. Дан напор в точке М. Определить расход в магистрали Q и расходы в каждой ветви.
Обе задачи решают на основе одной и той же системы уравнений, число которых на единицу больше числа конечных ветвей, а именно:
уравнение расходов:
Q = QB = QD = QE
уравнение равенства потребных напоров для ветвей CD и CE
Hст D + KCDQDт = Hст E + KCEQEт
уравнение равенства потребных напоров для ветви АВ и сложного трубопровода АСЕD
Hст B + KABQBт = Hст D + KCDQDт + KAC(QD + QE)т
выражение для потребного напора в точке М

Расчет сложных трубопроводов часто выполняют графоаналитическим способом, т.е. с применением кривых потребного напора и характеристик трубопроводов. Кривую потребного напора для сложного трубопровода следует строить следующим образом:
1) сложный трубопровод разбивают на ряд простых;
2) строят кривые потребных напоров для каждого из простых трубопроводов;
3) складывают кривые потребных напоров для ветвей (и параллельных линий, если они имеются) по правилу сложения характеристик параллельных трубопроводов;
4) полученную кривую складывают с характеристикой последовательно присоединенного трубопровода по соответствующему правилу (см. п.6.2).
Таким образом, при расчете идут от конечных точек трубопровода к начальной точке, т.е. против течения жидкости.
Дата добавления: 2018-02-15; просмотров: 955; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
