Способы решения матричных игр

Перед тем, как решать игру m´n, нужно, прежде всего попытаться ее упростить, избавившись от лишних стратегий.

Часто при нахождении решения матричной игры существенно помогает выявление превосходства одной стратегии над другой.

Определение.

Если для i-й и k-й стратегий первого игрока выполняются соотношения

a_ij ³ a_kj (j = 1, 2, …, n),

причем хотя бы одно из неравенств является строгим, то говорят, что стратегия i превосходит или доминирует стратегию k.

Аналогично для второго игрока: стратегия j доминирует стратегию r, если выполняются неравенства

a_ij ³ a_ir (i = 1, 2, …, m),

причем хотя бы одно из неравенств является строгим неравенством.

Использование соотношения доминирования позволяет сократить размерность матрицы выигрышей в матричной игре. Это свойство формулируется в виде следующей теоремы.

Теорема 1.

Пусть Г – матричная игра с матрицей А порядка m´n, и i-я стратегия первого игрока доминирует k-ю стратегию. Пусть А¹ матрица, получаемая из А путем исключения из нее k-й строки, и пусть Г¹ – матричная игра с матрицей А¹.

Тогда цена игры Г¹ совпадает с ценой игры Г, всякая оптимальная смешанная стратегия второго игрока в Г¹ есть также его оптимальная смешанная стратегия в игре Г, если u = (u₁, u₂, …, u_k_–1, u_k₊₁, …, u_m) есть оптимальная смешанная стратегия первого игрока в игре Г¹, то его смешанная стратегия х = (u₁, u₂, …, u_k_–1, 0, u_k₊₁, …, u_m) является оптимальной в игре Г.

Из теоремы следует, что если i-я стратегия первого игрока доминирует k-ю стратегию, то i-я стратегия для первого игрока лучше, чем k-я , т.е. первому игроку не выгодно использовать свою k-ю стратегию и она не должна входить в его оптимальную стратегию. Следовательно, вероятность применения k-й чистой стратегии в оптимальной смешанной стратегии первого игрока должна равняться нулю. Вычеркивая из А эту k-ю строку, получаем матрицу А¹, в которой количество строк на единицу меньше. При этом полагаем x_k = 0, где x_k – k-я компонента х. Игру с матрицей А¹ решать легче, так как в ней меньше строк. Если в матрице А¹ наблюдается доминирование стратегий первого игрока, то далее можно поступать аналогично и таким образом уменьшить размерность матрицы А¹.

Доминирование стратегий для второго игрока также дает дополнительные возможности для сокращения размера матрицы выигрышей.

С этой целью можно использовать следующее свойство.

Теорема 2.

Пусть Г матричная игра с матрицей А. Пусть q-я чистая стратегия второго игрока доминирует r-ю, матрица А¹ получена из А исключением q-го столбца, Г¹ – матричная игра с матрицей А¹. Тогда цена игры Г¹ такая же, как цена игры Г; всякая оптимальная смешанная стратегия первого игрока в Г¹ есть также его оптимальная смешанная стратегия в Г; если w = (w₁, w₂, ..., w_q_–1, w_q₊₁, ..., w _n) есть оптимальная смешанная стратегия второго игрока в Г¹, то у = (w₁, w₂, ..., w_q_–1, 0, w_q₊₁, ..., w _n) есть оптимальная смешанная стратегия второго игрока в Г.

Таким образом, из теоремы 2 следует, что, если q-я чистая стратегия второго игрока доминирует какую-либо его чистую стратегию, то q-й столбец в А можно вычеркнуть, положив y_q = 0, где y_q – q-я компонента оптимальной смешанной стратегии второго игрока. В результате, получаем матрицу А¹ меньшей размерности чем А. Если в А¹ есть доминирование стратегий, то можно поступать с ней аналогично и уменьшить ее размерность.

Пример 1.

А =	4	3	5	1
	4	5	3	5
	5	3	5	3
	1	5	4	8

Обозначим оптимальные смешанные стратегии первого и второго игроков соответственно через х и у. Очевидно, третья стратегия первого игрока доминирует его первую стратегию, поэтому можно в матрице А вычеркнуть первую строку, положив х₁ = 0. Тогда получим новую матрицу

А¹ =	4	5	3	5
	5	3	5	3
	1	5	4	8

в которой 4-я стратегия второго игрока доминирует его 2-ю стратегию, и поэтому вычеркиваем четвертый столбец, полагая y₄ = 0, и получаем новую матрицу

А² =	4	5	3
	5	3	5
	1	5	4

В этой матрице уже нет доминирования. Таким образом, исходную игру с матрицей порядка 4´4 с помощью доминирования свели к игре с матрицей порядка 3´3.

Пример 2.

Рассмотрим игру со следующей матрицей:

5 2 1

2 1 3

3 6 4

Третья строка этой матрицы доминирует вторую. Исключение второй строки приводит к матрице

5 2 1

3 6 4

Третий столбец в этой урезанной матрице доминирует второй, и исключение второго столбца дает

5 1

3 4

В итоге, если можно найти решение для полученной игры, то его легко использовать для решения исходной игры, просто приписав исключенным строкам и столбцам нулевые вероятности.

Матричные игры обладают еще одним интересным свойством, которое формулируется в виде следующей теоремы.

Теорема 3.

Пусть дана матричная игра Г с матрицей А = (a_ij) и с ценой игры v. Тогда оптимальные смешанные стратегии игроков матричной игры Г_В с матрицей В = (b_ij) = (da_ij + с), где d > 0 совпадают с оптимальными смешанными стратегиями соответствующих игроков в матричной игре Г, а цена игры Г_В равна v_B = dv + с.

Пользуясь теоремой 3, можно несколько упрощать элементы матрицы А с тем, чтобы легче было с ними оперировать при нахождении решения игры.

Пример.

Рассмотрим матричную игру с матрицей

А =	200	300
А =	600	100

Если каждый элемент этой матрицы разделить на 100 и затем из полученных элементов вычесть 1, то получим игру с матрицей

В =	1	2
В =	5	0

которая имеет более простые элементы. Здесь проведено следующее преобразование:

b_ij = 0,01×a_ij – 1, т.е. d = 0,01, c = –1.

В этой игре нет седловой точки в чистых стратегиях. Поэтому для решения игры с матрицей В обозначим через х = (x₁, x₂), у = (y₁, у₂) оптимальные смешанные стратегии соответственно первого и второго игроков, v – цена игры с матрицей A, v_B – цена игры с матрицей В.

Согласно следствию из теоремы 1, х и у должны удовлетворять соотношениям:

x₁ + 5x₂ ³ v_B y₁ + 2y₂ £ v_B

2x₁ ³ v_B 5y₁ £ v_B

x₁ + x₂ = 1 y₁ + y₂ = 1

Предположим, что все эти неравенства являются равенствами. Позже будет показано, что это всегда так, если в матричной игре с матрицей порядка 2´2 нет седловой точки в чистых стратегиях. Тогда получим

x₁ + 5x₂ = v_B y₁ + 2y₂ = v_B

2x₁ = v_B 5y₁ = v_B

x₁ + x₂ = 1 y₁ + y₂ = 1

Решив данную систему, получим:

v_B = 3/5, x₁ = 3/10, x₂ = 7/10, y₁ = 3/25, y₂ = 22/25

Тогда решением матричной игры с матрицей А будет

Замечание.

Отметим, что исключение доминируемых (не строго!) стратегий может привести к потере некоторых решений. Если же исключаются только строго доминируемые стратегии, то множество решений игры не изменится.

Пример 3.

Пусть G = (Х,Y,А), где Х = {1, 2, 3, 4}; Y = {1, 2, 3, 4}, а функция выигрыша А задана следующим образом:

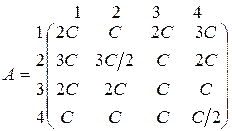
где С > 0.

Решение.

Прежде всего заметим, что по теореме 3 достаточно решить игру G¹ = (Х, Y, А), где А¹ = А . В матричной форме игра G¹ определяется матрицей выигрышей

Элементы четвертой строки этой матрицы “ £ ” соответствующих элементов третьей строки и поэтому третья стратегия игрока 1 доминирует над четвертой. Кроме того, элементы первого столбца матрицы А¹ “ ³ ” соответствующих элементов второго столбца, Следовательно, вторая стратегия игрока 2 доминирует над его первой стратегией.

Далее, из теоремы 1 и 2 следует, что всякое решение игры

G² = (Х \{4}, Y \{1}, А¹)

является решением игры G¹. В матричной форме игру G² можно представить матрицей

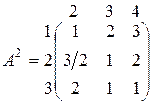Очевидно, что элементы второй строки “ ³” полусуммы соответствующих элементов первой и третьей строк. Кроме того, элементы третьего столбца матрицы А² “ ³“ соответствующих элементов второго столбца. Применяя теорему3, получим, что всякое решение игры

G ³ = (Х \ {4,2}, Y \ {1,4}, А²)

является решением игры G², а следовательно и игры G¹. Игра G³ определяется матрицей

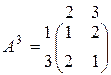Матрица А³не имеет седловой точки, т.к. не выполнено равенство

= ,

а игра G³ не имеет решения в чистых стратегиях, т.е. оптимальные стратегии игроков являются смешанными. Эти стратегии (в данном случае) легко найти из анализа структуры матрицы А³. Поскольку матрица А³симметрична, можно предположить, что игроки в оптимальной стратегии используют свои чистые стратегии с равными вероятностями.

Действительно, если игрок 1 выбирает с равными вероятностями стратегии 1 и 3, то при применении любой из двух чистых стратегий игроком 2 математическое ожидание выигрыша игрока 1 будет равным либо

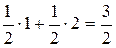, либо .

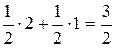Аналогично, если игрок 2 использует свои чистые стратегии 2 и 3 с равными вероятностями, то математическое ожидание его проигрыша будет равно 3/2. Следовательно, указанные стратегии являются оптимальными в игре G³, а величины 3/2 – значением игры G³. Из предыдущего следует, что эти стратегии оптимальны и в G¹.

Таким образом, стратегия Х = (1/2, 0, 1/2, 0) является оптимальной стратегией игрока 1, стратегия Y = (0, 1/2, 1/2, 0) – оптимальной стратегией игрока 2 в игре G¹, а значение игры G¹ равно 3/2. В силу свойства 4 решением игры G будет тройка (Х, Y,3С/2).

Решение антагонистических игр 2×2 в смешанных стратегиях

Если игра 2×2 имеет седловую точку, то ее решение очевидно.

Пусть игра 2×2 не имеет седловой точки. Требуется найти цену игры v и оптимальные смешанные стратегии обоих игроков:

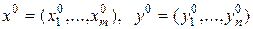Чистые стратегии, входящие в оптимальную стратегию с положительными вероятностями, называются активными стратегиями.

Для решения матричных игр 2´2 можно использовать аналитический и геометрический методы.

Аналитический метод

Теорема об активных стратегиях

Пусть v – цена игры, и – оптимальные стратегии игроков. Тогда справедливы следующие утверждения:

– для любой активной стратегии i первого игрока выполняется равенство

E(i, y⁰) = v;

– для любой активной стратегии j второго игрока имеет место равенство

E(x⁰, j) = v.

В игре 2×2 все стратегии игроков являются активными (почему?)

Выигрыш игрока первого игрока, если он применяет оптимальную стратегию х⁰, а второй игрок свою активную стратегию 1 равен

По теореме об активных стратегиях этот выигрыш равен цене игры, т.е.

Аналогично для случая, когда первый игрок применяет оптимальную стратегию х⁰, а второй игрок активную стратегию 2:

Получаем:

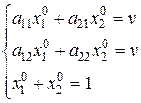(1)

Получили систему уравнений относительно .

Аналогичную систему получим для оптимальных стратегий второго игрока:

(2)

Решая эти системы, найдем неизвестные оптимальные стратегии игроков х⁰, у⁰ и цену игры v.

Цена игры ν общая для обоих игроков, поэтому при решении систем уравнений (1) и (2) должно получиться одинаковое значение ν.

Решение игры 2´2 в общем виде выглядит следующим образом

; х₂ = 1 – х₁;

; у₂ = 1 – у₁; (***)

Геометрический метод

Рассмотрим геометрическую интерпретацию игры 2×2.

Пусть игрок А применяет смешанную стратегию, а игрок В – активную стратегию В₁. Тогда средний выигрыш игрока А будет:

Мы получили уравнение прямой, которую обозначим В₁, т.к. она соответствует активной стратегии В₁ игрока В.

Если игрок В применяет свою активную стратегию В₂, а игрок А стратегию (х, (1 – х)), то выигрыш игрока А равен:

Видно, что какую бы стратегию ни применил В, игрок А гарантирует себе выигрыш не меньше, чем ордината ломаной В₂МВ₁.

Ломанная В₂МВ₁ (на рис. выделена полужирно) определяет минимальные возможные средние выигрыши игрока А при использовании им своих смешанных стратегий. Точка М (самая высокая точка ломанной) – определяет наилучший средний выигрыш игрока А из всех минимальных. Она соответствует оптимальной смешанной стратегии игрока А. При этом: если М имеет координаты (х, у), то р₁ = 1 – х, р₂ = х, ν = y.

Таким образом, задача сводится к нахождению координат точки М, которая является точкой пересечения прямых В₁В₁ и В₂В₂. Для нахождения уравнений прямых В₁В₁ и В₂В₂.можно воспользоваться уравнением прямой, проходящей через две точки:

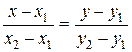с учетом того, что прямую В₁В₁ определяют точки (0; a₁₁), (1; а₂₁), а прямую В₂В₂ определяют точки (0; a₁₂), (1; а₂₂).

Для игрока В оптимальная смешанная стратегия находится аналогично, но точка М определяется не самой высокой точкой нижней ломанной, а самой низкой точкой высокой ломанной – полужирная ломанная на рисунке 2.

Пусть В применяет стратегию Y = (у, (1 – у)), а А применяет стратегию А₁. Тогда проигрыш игрока В определяется точками прямой:

Эту прямую обозначим А₁. Если А применяет стратегию А₂, а В стратегию Y, то проигрыш В лежит на прямой А₂:

Из графика видно, что какую бы стратегию ни применял игрок А, игрок В гарантирует себе проигрыш не более, чем ордината ломаной А₁МА₂.

Оптимальной стратегией игрока В будет такая стратегия Y = (у, (1 – у)), при которой ордината ломаной линии А₁МА₂ будет минимальна. Найдя координаты точки М (х, у), как точки пересечения прямых А₁А₁ и А₂А₂, компоненты оптимальной смешанной стратегии игрока В и цену игры: Y*(у₁, у₂), ν можно найти по следующим формулам:

q₁ = 1 – x, q₂ = x, ν = y.

Пример.

Решить игру с матрицей платежей

Пусть оптимальная смешанная стратегия игрока А есть .

Тогда:

Найдем оптимальную смешанную стратегию игрока В.

Игру можно решить графически.

Пример.

Решить графически игру с матрицей А

Решение антагонистических игр m×2

Найдем решение игры со следующей матрицей

Пусть игрок В применяет смешанную стратегию Y = (у, (1 – у)), а игрок А – чистую стратегию A_i (i = 1, …, m). Тогда средний проигрыш игрока В будет:

Z = a_i₁×у + a_i₂×(1 – у)

Это уравнение прямой, которую обозначим A_i.

Для i = 1, …, m, построим все прямые А₁, А₂, …, А _m. Проигрыш игрока В будет не больше максимального значения ординат прямых А₁, А₂, …, А _m, т.е. не больше ординат ломаной MNKC. Оптимальной стратегией игрока В будет такая смешанная стратегия, при которой его максимально возможный проигрыш будет минимальным, т.е. будет минимальна ордината ломаной MNKC. Это точка у⁰, и оптимальная стратегия (у⁰, (1 – у⁰)). Цена игры – ордината точки N.

В качестве активных стратегий игрока А можно выбрать две чистых стратегии, соответствующие прямым, пересекающимся в N. Пусть это A_i и A_j.

Из матрицы исходной игры вычеркнем все строки кроме i-ой и j-ой, т.е. получим матрицу:

Тогда оптимальную смешанную стратегию игрока А X⁰ = (х⁰, (1 – х⁰) ) можно определить как для игры 2´2, т.е. из соотношений

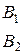
Тогда: Х⁰ = (0, …, 0, х⁰, 0, …, 0, 1 – х⁰, 0, …, 0)

i-я компонента j-я компонента

Пример 1:

А₁ : 4y + 3 (1 – y) = z

A₂ : 2y + 4 (1 – y) = z

A₃ : 5 (1 – y) = z

A₄ : –y + 6 (1 – y) = z

В точке N пересекаются прямые А₁ и А₄, т.е.

4y + 3 (1 – y) = –y + 6 (1 – y)

y⁰ = 3/8, Y⁰ = (3/8, 5/8)

v = 4×3/8 + 3×(1 – 3/8) = 27/8

Поскольку активными стратегиями А являются А₁ и А₄, то

Отсюда получаем В₁ : 4x⁰ – (1 – x⁰) = z⁰ = v

В₂ : 3x⁰ + 6 (1 – x⁰) = z⁰ = v

Или 4x⁰ – (1 – x⁰) = 3x^* + 6 (1 – x⁰)

x⁰ = 7/8, 1 – x⁰ = 1/8

Тогда Х⁰ = (7/8, 0, 0, 1/8).

Решение антагонистических игр 2× n

Рассмотрим матрицу игры 2×n:

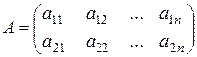
Пусть игрок А применяет смешанную стратегию (х, 1–х), а игрок В – активную стратегию B_j (j = 1, …, n).

В _i : z = a₁_i x + a₂_i(1 – x)

Изобразим прямые В₁, …, В_n на плоскости. Какую бы стратегию ни применил игрок В, игрок А получит выигрыш не менее ординаты ломаной линии MNKC.

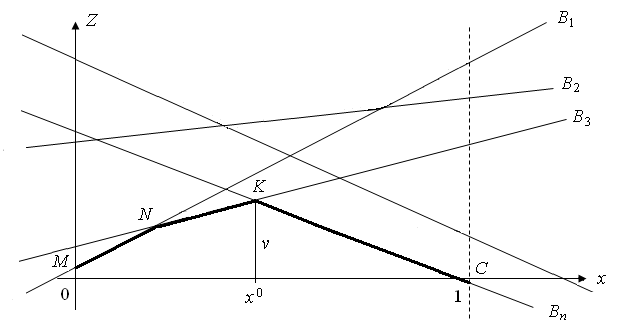
Оптимальная смешанная стратегия первого игрока есть такая смешанная стратегия, при которой он получает максимальный гарантированный выигрыш. На рис. это точка х⁰, которая соответствует max из ординат ломаной MNKC. Поэтому оптимальная стратегия игрока А:

Х⁰ = (x⁰, (1 – x⁰)),

а цена игры v равна ординате точки К. В качестве активных стратегий игрока В можно выбрать две чистых стратегии, соответствующих любым двум прямым, пересекающимся в точке К. Пусть это В_i и В_j. Тогда матрицу исходной игры можно записать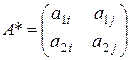

Оптимальную смешанную стратегию игрока В найти как в игре 2´2

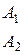
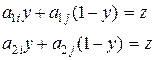
Тогда: Y⁰ = (0, …, 0, у⁰, 0, …, 0, 1 – у⁰, 0, …, 0)

i-я компонента j-я компонента

Пример 2:

В₁ : 2x + 4 (1 – x) = z

В₂ : 3x + 2 (1 – x) = z

В₃ : x + 3 (1 – x) = z

В₄ : 4x + (1 – x) = z

В точке N пересекаются прямые В₃ и В₄, т.е. x + 3 (1 – x) = 4x + (1 – x), т.е.

x⁰ = 2/5, Х⁰ = (2/5, 3/5)

v = 2/5 + 3 × 3/5 = 11/5

Активными стратегиями игрока В будут В₃ и В₄, т.е.

Тогда А₁ : y + 4 (1 – y) = z

A₂ : 3y + (1 – y) = z

y⁰ = 3/5 Y⁰ = (0, 0, 3/5, 2/5)

Пример 1.

Решить графическим методом игру .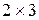

Пусть первый игрок придерживается смешанной стратегии

а второй игрок – одной из своих чистых стратегий.

Тогда

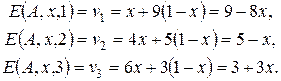
Построим прямые , определяющие график функции

В точке максимума , т.е.

Активными стратегиями второго игрока являются вторая и третья стратегии, поэтому оптимальную стратегию этого игрока ищем в виде

Для этого решим игру с матрицей

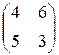По формуле (***) имеем .

Итак,

Пример 2

Решить игру, заданную платёжной матрицей.

Ответ: Х = ( ; 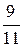), при цене игры v = 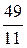. Y = (0; ; ).

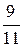Пример 3 . Найти решение игры, заданной матрицей

Ответ: U = ( 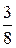; ); Х = ( ; 0; 0; ); u = .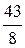

Решение антагонистических игр m´n.
Сведение матричной игры к задаче линейного программирования

Пусть дана игра m´n в нормальной форме, т.е.

Будем считать, что все элементы матрицы больше 0. Если это не так, то ко всем элементам можно прибавить такое число L>0, например,

где r > 1, чтобы все элементы стали положительными. При этом цена игры возрастает на L, но оптимальные стратегии не меняются. Т.о. a_ij >0, значит, v > 0

Пусть игрок А применит свою оптимальную стратегию . Тогда его выигрыш будет не менее v при любых действиях игрока В. В частности, если игрок В применит свою чистую стратегию В _j, то выигрыш А составит:

j = (1, …, n)

Поделим это неравенство на v и, обозначив

(i = 1, …, m),

получим:

z_i >= 0 j = (1, …, n)

Вероятности (i = 1, …, m) должны удовлетворять условию

Поделим это выражение на v и в новых обозначениях запишем

Поскольку игрок А стремиться к максимуму v, то целевая функция будет иметь вид:

Т.о. имеем:

(1)

Задача (1) – задача линейного программирования.

Пусть 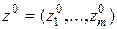– решение задачи (1).

Тогда

; (i = 1, …, m).

Аналогичные рассуждения можно проделать для игрока В:

Пусть он применяет оптимальную смешанную стратегию , а игрок А – чистую стратегию А _i (i = 1, …, m). Тогда проигрыш игрока В составит величину не более v:

(i = 1, …, m).

Разделим это неравенство на v > 0 и, обозначив

(j = 1, …, n), получим .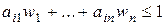

Вероятности (i = 1, …, m) должны удовлетворять условию

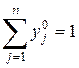Поделим это выражение на v и в новых обозначениях получим:

Поскольку игрок В стремиться минимизировать проигрыш, т.е.

v ® min,

получим функцию

Т.о. имеем задачу линейного программирования:

(2)

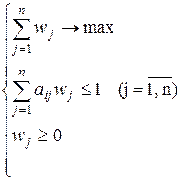
Пусть – решение (2).

Тогда

Легко видеть, что задачи (1) и (2) представляют собой пару взаимодвойственных задач линейного программирования. Т.о., решение антагонистической игры m´n можно найти путем решения пары взаимодвойственных задач линейного программирования.

Пример

Две отрасли могут осуществлять капитальные вложения в 3 объекта. Стратегии отраслей: i-я стратегия состоит в финансировании i-го объекта (i = 1, 2, 3). Учитывая особенности вкладов и местные условия, прибыли первой отрасли выражаются следующей матрицей:

Величина прибыли первой отрасли считается такой же величиной убытка для второй отрасли - представленная игра может рассматриваться как игра двух игроков с нулевой суммой.

Рассмотрим игрока А. Будем искать оптимальную смешанную стратегию игрока А: Х ( х₁, х₂, х₃), где х _i – частота (вероятность) использования игроком А своей i-стратегии ( i = 1, 2, 3).Обозначим цену игры (средний выигрыш) – v.

Чтобы свести матричную игру для игрока А к задаче линейного программирования преобразуем платежную матрицу так, чтобы все ее элементы были больше нуля – прибавим ко всем элементам матрицы число 4. Получаем преобразованную платежную матрицу:

Дата добавления: 2021-04-05; просмотров: 182; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 45

Мы поможем в написании ваших работ!