Решение матричных игр в чистых стратегиях
Главным в исследовании игр является понятие оптимальных стратегий игроков. В это понятие интуитивно вкладывается такой смысл:
Стратегия игрока является оптимальной, если применение этой стратегии обеспечивает ему наибольший гарантированный выигрыш при всевозможных стратегиях другого игрока.
Каждая стратегия игрока i = 1, 2, …, m; j = 1, 2, ..., n часто называется чистой стратегией.
Рассмотрим прямоугольную игру m´n с матрицей выигрышей А.
| А = | а11 | … | a1j | … | а1n |
| … | … | … | … | … | |
| ai1 | … | aij | … | ain | |
| … | … | … | … | … | |
| am1 | … | amj | … | amn |
Исследуем матрицу выигрышей с точки зрения первого игрока. Если он выберет стратегию 1, то ему будет заплачено как минимум min а1j. Если он выберет i-ю стратегию, ему будет заплачено, по меньшей мере, min aij (i = 1, …, m). Таким образом, он должен выбрать такую стратегию, чтобы min aij был как можно больше, т.е. выбор i-ой стратегии осуществляется как
.
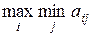Аналогично, платежи второму игроку – это элементы матрицы А со знаком минус, т.е. для второго игрока существует выбор, который гарантирует ему, что он получит по меньшей мере
.
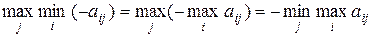Таким образом, первый игрок может гарантировать себе выигрыш 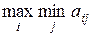, а второй может играть так, что первый не выиграет у него больше, чем 
.
Для нахождения гарантированного выигрыша первого игрока для каждого значения i (i = 1, 2, ..., m) определяется минимальное значение выигрыша в зависимости от применяемых стратегий второго игрока
|
|
|
(i = 1, 2, ..., m),
т.е. определяется минимальный выигрыш для первого игрока при условии, что он применит свою i-ю чистую стратегию, затем из этих минимальных выигрышей отыскивается такая стратегия i = i0, при которой этот минимальный выигрыш будет максимальным, т.е. находится
. (1)
Такая стратегия называется максиминной.
Определение.
Число a, определенное по формуле (1), называется нижней чистой ценой игры и показывает, какой минимальный выигрыш может гарантировать себе первый игрок, применяя свои чистые стратегии при всевозможных действиях второго игрока.
Второй игрок при оптимальном своем поведении должен стремиться по возможности за счет своих стратегий максимально уменьшить выигрыш первого игрока. Поэтому для второго игрока отыскивается
т.е. определяется максимальный выигрыш первого игрока, при условии, что второй игрок применит свою j-ю чистую стратегию, затем второй игрок отыскивает такую свою j = j1 стратегию, при которой первый игрок получит минимальный выигрыш, т.е. находит
(2)
Такая стратегия называется минимаксной.
|
|
|
Определение.
Число b, определенное по формуле (2), называется чистой верхней ценой игры и показывает, какой максимальный выигрыш за счет своих стратегий может гарантировать себе первый игрок. Другими словами, применяя свои чистые стратегии, первый игрок может обеспечить себе выигрыш не меньше a, а второй игрок за счет применения своих чистых стратегий может не допустить выигрыш первого игрока больше, чем b.
Нижняя (a) и верхняя (b) цены игры всегда связаны соотношением 
.
Определение.
Если в игре с матрицей А нижняя и верхняя чистые цены игры совпадают, т.е.
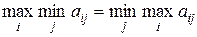(a = b),
то говорят, что эта игра имеет седловую точку в чистых стратегиях и чистую цену игры:
v = a = b. (3)
Ситуация (i0, j0) называется равновесной, цена игры совпадает с элементом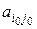 
платежной матрицы v = 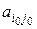, элемент 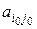называется седловым элементом матрицы или точкой равновесия.
Определение.
Седловая точка – это пара чистых стратегий (i0, j0) соответственно первого и второго игроков, при которых достигается равенство a = b.
В понятие седловой точки вложен следующий смысл: если один из игроков придерживается стратегии, соответствующей седловой точке, то другой игрок не сможет поступить лучше, чем придерживаться стратегии, соответствующей седловой точке. Имея в виду, что лучшее поведение игрока не должно приводить к уменьшению его выигрыша, а худшее – может приводить к уменьшению его выигрыша, эти условия можно записать математически в виде следующих соотношений:
|
|
|
(4)
где i, j – любые чистые стратегии соответственно первого и второго игроков; (i0, j0) – стратегии, образующие седловую точку.
Таким образом, исходя из (4), седловой элемент 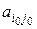является минимальным в i0-й строке и максимальным в j0-м столбце в матрице А.
Отыскание седловой точки матрицы А происходит следующим образом: в матрице А последовательно в каждой строке находят минимальный элемент и проверяют, является ли этот элемент максимальным в своем столбце. Если он является таковым, то он и есть седловой элемент, а пара стратегий, соответствующая ему, образует седловую точку.
Пара чистых стратегий (i0, j0) первого и второго игроков, образующая седловую точку и седловой элемент 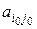, называется решением игры.
Чистые стратегии i0 и j0, образующие седловую точку, называются оптимальными чистыми стратегиями соответственно первого и второго игроков.
|
|
|
Итак, если платежная матрица такова, что (3) имеет место, то поиск оптимального способа игры заканчивается. Но далеко не для всех матриц данное условие выполняется, т.е. не у всех матриц существует седловая точка.
Пример 1.
| min | |||
| А= | 1 | –1 | –1 |
| –1 | 1 | –1 | |
| max | 1 | 1 |
. Седловой точки нет.
Пример 2.
Найти решение игры
| min | ||||
| А= | 21 | 11 | 31 | 11 |
| 32 | 0 | 4 | 0 | |
| max | 32 | 11 | 31 |
(1, 2) – седловая точка (значение 11).
Оптимальная чистая стратегия первого игрока – первая (i0 = 1), оптимальная чистая стратегия второго игрока – вторая (j0 = 2), цена игры равна 11 (v = 11).
Пример 3.
Найти решение игры
| min | ||||
| А= | 12 | 13 | 12 | 12 |
| 10 | 31 | 9 | 9 | |
| max | 12 | 31 | 12 |
Две седловые точки (1, 1) и (1, 3) (значение 12).
В этой игре два оптимального решения: i0 = 1, j0 = 1, v = 12;
i0 = 1, j0 = 3, v = 12.
Пример 4
Найти решение игры
| min | ||||
| А= | 1 | –3 | –2 | –3 |
| 0 | 5 | 4 | 0 | |
| 2 | 3 | 2 | 2 | |
| max | 2 | 5 | 4 |
Седловой точкой является пара (i0 = 3; j0 = 1), при которой v = a = b = 2.
Заметим, что хотя выигрыш в ситуации (3;3) также равен 2 = a = b, она не является седловой точкой, т.к. этот выигрыш не является максимальным среди выигрышей третьего столбца.
Пример 5
Найти решение игры
| min | |||
| А= | 10 | 30 | 10 |
| 40 | 20 | 20 | |
| max | 40 | 30 |
Из анализа матрицы выигрышей видно, что a < b, т.е. данная матрица не имеет седловой точки.
Пример 6 . Сражение в море Бисмарка.
В 1943 году японский адмирал Кимура получил приказ переправить военный контингент через море Бисмарка к Новой Гвинее. Американский генерал Кинни получил приказ на перехват и бомбардировку японского флота. Кимура имел выбор между двухдневным маршрутом (северным) и трехдневным (южным). В свою очередь Кинни должен был решить, по какому маршруту послать самолеты в поисках японского транспорта: северному или южному. В случае ошибки самолеты возвращались в конце дня на свои базы и на следующий день могли быть посланы по другому маршруту.
Описанная ситуация может быть представлена следующей матрицей:
| Кимура | |||
| север | юг | ||
| Кинни | север | 2, –2 | 2, –2 |
| юг | 1, –1 | 3, –3 | |
Выигрыши: (Кинни, Кимура).
Поскольку мы имеем игру с нулевой суммой, то ее можно свести к антагонистической игре с матрицей:
| min | |||
| А= | 2 | 2 | 2 |
| 1 | 3 | 1 | |
| max | 2 | 3 |
Будем искать решение в чистых стратегиях:
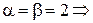игра имеет седловую точку: (Север, Север).
Пример 7
Найти решение игры
| min | |||||
| А= | 5 | 3 | 4 | 3 | 3 |
| 7 | 2 | 0 | –2 | –2 | |
| 10 | –1 | –4 | 2 | –4 | |
| max | 10 | 3 | 4 | 3 |
Игра имеет два решения: i0 = 1, j0 = 2, v = 3
i0 = 1, j0 = 4, v = 3
Дата добавления: 2021-04-05; просмотров: 204; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!