Оптимальные смешанные стратегии
Исследование в матричных играх начинается с нахождения ее седловой точки в чистых стратегиях. Если матричная игра имеет седловую точку в чистых стратегиях, то нахождением этой седловой точки заканчивается исследование игры. Если же в игре нет седловой точки в чистых стратегиях, то можно найти нижнюю и верхнюю чистые цены этой игры, которые указывают, что первый игрок не должен надеяться на выигрыш больший, чем верхняя цена игры, и может быть уверен в получении выигрыша не меньше нижней цены игры.
В случае отсутствия ситуации равновесия
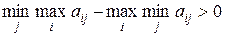
и максиминная и минимаксная стратегии не являются оптимальными. Более того, игрокам бывает невыгодно их придерживаться, так как они могут получить больший выигрыш. Однако сообщение о выборе стратегии противнику может привести к еще большим потерям, чем в случае максиминной или минимаксной стратегии.
Пример
Найти решение игры
| min | |||
| А= | 7 | 3 | 3 |
| 2 | 5 | 2 | |
| max | 7 | 5 |
Для такой матрицы a = 3, а b = 5, т.е. данная матрица не имеет седловой точки (нет ситуации равновесия). Обозначим через i0 максиминную стратегию первого игрока (i0 = 1), а минимаксную стратегию второго игрока через j0 (j0 = 2). Пусть второй игрок придерживается стратегии j0 = 2, а первый игрок выберет стратегию i = 2. Тогда последний получит выигрыш 5, т.е. на 2 единицы больше, чем максимин. Однако если второй игрок догадается о выборе первого игрока, то он изменит стратегию на j = 1, и тогда первый получит выигрыш лишь 2 единицы, т.е. на единицу меньше, чем в случае максимина. Аналогичные рассуждения можно провести и для второго игрока.
|
|
|
При многократном повторении матричных игр без седловой точки в виде партий игроки каждый раз применяют свои стратегии таким образом, что их противники не догадываются об их содержании, и на этом пути в среднем достигают определенных выигрышей, сыграв всю серию партий. Эти выигрыши в среднем больше нижней цены игры и меньше верхней цены игры. Чем больше это среднее значение, тем лучше стратегии применяет игрок.
Поэтому игрокам целесообразно выбирать свои стратегии случайно, с определённой вероятностью, т.е. определять распределение вероятностей на множестве чистых стратегий, а затем предоставить выбор конкретной чистой стратегии случайному механизму.
Выбор игроками своих чистых стратегий с некоторыми наперед заданными вероятностями тоже является некоторой стратегией. В отличие от чистых стратегий, такие стратегии называются смешанными.
Определение.
Смешанной стратегией игрока называется полный набор вероятностей применения его чистых стратегий.
Таким образом, если первый игрок имеет m чистых стратегий 1, 2, ..., m, то его смешанная стратегия x – это набор чисел (вероятностей) x = (x1, х2, ..., xm), удовлетворяющих соотношениям
|
|
|
xi ³ 0 (i = 1, …, m),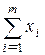 
= 1.
Аналогично для второго игрока, который имеет n чистых стратегий, смешанная стратегия y – это набор чисел (вероятностей)
y = (y1, ..., yn), yj ³ 0, (j = 1, …, n),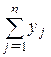 
= 1.
Так как каждый раз применение игроком одной чистой стратегии исключает применение другой, то чистые стратегии являются несовместными событиями. Кроме того, они являются единственными возможными событиями.
Чистая стратегия есть частный случай смешанной стратегии. Действительно, если в смешанной стратегии какая-либо i-я чистая стратегия применяется с вероятностью 1, то все остальные чистые стратегии не применяются. И эта i-я чистая стратегия является частным случаем смешанной стратегии. Для соблюдения секретности каждый игрок применяет свои стратегии независимо от выбора другого игрока.
Определение.
Средний выигрыш первого игрока в матричной игре с матрицей А выражается в виде математического ожидания его выигрышей
E (A , x , y) = 
= x A yT
Первый игрок имеет целью за счёт изменения своих смешанных стратегий х максимально увеличить свой средний выигрыш Е (А, х, y), а второй – за счёт своих смешанных стратегий стремится сделать Е (А, х, y) минимальным, т.е. для решения игры необходимо найти такие х и y, при которых достигается верхняя цена игры
|
|
|
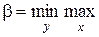Е (А, х, y).
С другой стороны, ситуация должна быть аналогичной относительно второго игрока, т.е. нижняя цена игры должна быть
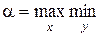Е (А, х, y).
Подобно играм, имеющим седловые точки в чистых стратегиях, вводится следующее определение:
Оптимальными смешанными стратегиями первого и второго игроков называются такие наборы хо, уо соответственно для первого и второго игроков, которые удовлетворяют равенству
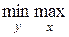Е (А, х, y) = 
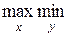Е (А, х, y) = Е (А, хо, уо).
Величина Е (А, хо, уо) называется при этом ценой игры и обозначается через v.
Имеется и другое определение оптимальных смешанных стратегий: хо, уо называются оптимальными смешанными стратегиями соответственно первого и второго игроков, если они образуют седловую точку:
Е (А, х, уо) £ Е (А, хо, уо) £ Е (А, хо, у)
Оптимальные смешанные стратегии и цена игры называются решением матричной игры.
Пример.
Рассмотрим прямоугольную игру.
| Р2 | |||
| 1 | 2 | ||
| Р1 | 1 | 1 | –1 |
| 2 | –1 | 1 | |
|
|
|
Поскольку матрица не имеет седловой точки, оптимальное поведение для Р1 и Р2 нам не известно. Для Р1 безразлично, что выбрать: 1 или 2, т.к. в обоих случаях он получает 1 или –1 в зависимости от выбора Р2.
С другой стороны, если Р2 знает, какой выбор сделал Р1, Р2 может поступить так, что Р1 заплатит ему 1.
Таким образом, для Р1 очень важно играть так, чтобы Р2 трудно было угадать, какой выбор сделал Р1. Одним из способов для Р1 является случайный выбор.
Допустим, что Р1 делает выбор, бросая монетку. Выбирает 1, если монетка упала гербом и 2, если решкой. В этом случае Р1 выбирает 1 с вероятностью 1/2 и 2 с такой же вероятностью 1/2.
Если Р2 выбирает 1, то математическое ожидание выигрыша для Р1 будет:
1/2 (1) + 1/2 (–1) = 1/2 – 1/2 = 0
Если Р2 выбирает 2, математическое ожидание выигрыша для Р1:
1/2 (–1) + 1/2 (1) = –1/2 + 1/2 = 0
Допустим, Р1 выбирает 1 с вероятностью х и 2 с вероятностью (1 – х). Математическое ожидание выигрыша для Р1, если Р2 выбирает 1, будет:
1×х + (–1)(1 – х) = 2х – 1.
Математическое ожидание выигрыша для Р1, если Р2 выбирает 2, будет:
(–1)×х + 1×(1 – х) = 1 – 2х.
Если x > 1/2, Р1 будет проигрывать Р2, если Р2 будет выбирать 2, т.к.
1 – 2х < 0 при х > 1/2.
Если x < 1/2, Р1 будет проигрывать Р2, если он выбирает 1, т.к.
2х – 1 < 0 при х < 1/2.
Отсюда следует, что оптимальный вариант игры Р1 выбирать 1 и 2 с вероятностью 1/2. Для Р2 оптимальный вариант тот же. Цена игры для Р1 (т.е. математическое ожидание выигрыша) равна 0.
Пример.
| у | 1 – у | |
| х | 1 | 3 |
| 1 – х | 4 | 2 |
Поскольку матрица не имеет седловой точки, первому и второму игрокам желательно выбирать альтернативы с определенными частотами.
Предположим, первый игрок выбирает стратегию 1 с частотой х, а стратегию 2 с частотой 1 – х, а второй игрок стратегию 1 выбирает с частотой у, а стратегию 2 с частотой 1 – у. Тогда математическое ожидание выигрыша для первого игрока:
Е(х, у) = 1×х×у + 3×х×(1 – у) + 4×(1 – х)×у + 2×(1 – х)(1 – у) =
= –4×х ×у + х + 2×у + 2 = –4×(х – 1/2)(у – 1/4) +5/2. (7)
Отсюда видно, что если первый игрок берет х = 1/2, то его выигрыш будет по крайней мере 5/2. Более того, он не может обеспечить себе выигрыш более 5/2, т.к. второй игрок, взяв у = 1/4 , может гарантировать, что выигрыш первого игрока будет 5/2.
Итак, первый игрок может ставить на 5/2 и получить эту сумму, играя х = 1/2. Второй игрок может примириться с тем, что он проиграет 5/2, и, играя у = 1/4, проиграть не более 5/2.
Следовательно, для этой игры оптимальный способ для первого игрока выбирать 1 и 2 стратегии одинаково часто, а для второго игрока выбрать стратегию 1 с вероятностью 1/4, а стратегию 2 с вероятностью 3/4, тогда 5/2 можно принять за цену игры.
Из равенства (7) мы находим для всех х и у:
Е(х, 1/4) £ Е(1/2,1/4) £ Е(1/2, у)
Это неравенство можно принять за определение оптимальных частот для любой игры 2´2.
Итак, если Е(х, у) – математическое ожидание выигрыша первого игрока, когда он выбирает 1 с частотой х, а 2 с частотой (1 – х), а второй игрок выбирает 1 с частотой у, а 2 с частотой (1 – у), то мы говорим, что х0 есть оптимальная частота первого игрока, а у0 – оптимальная частота для второго игрока, если для всех 0 £ х £ 1 и 0 £ у £ 1
Е(х, у0) £ Е(х0, у0) £ Е(х0, у)
Дата добавления: 2021-04-05; просмотров: 72; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!