Матричные антагонистические игры

ТЕОРИЯ ИГР

В практической деятельности людей часто возникают конфликтные ситуации, когда нескольким участникам приходится взаимодействовать при обстоятельствах, в которых каждый из участников старается достичь своей цели своим доступным ему способом, но никто из них полностью не влияет на ход событий, т.е. исход борьбы лишь частично зависит от действий каждого участника. В конфликтной ситуации имеются несколько заинтересованных сторон, каждая из которых старается получить максимальный выигрыш. Такие ситуации возникают во время проведения обычных настольных игр, спортивных состязаний, в военном деле, в торговых отношениях, в экономической, хозяйственной и политической деятельности, в медицинском обслуживании и т. д.

Теория игр – это раздел математики, в котором исследуются и вырабатываются оптимальные правила (стратегии) поведения для каждого из участников конфликтной ситуации.

Теория игр исследует ситуации, в которых принятие решений зависит от нескольких участников.

Теория игр является составной частью предмета исследование операций, изучающей теорию математических моделей принятия оптимальных решений. Задачи исследования операций классифицируются по уровню информации о ситуации, которой располагает субъект, принимающий решение. Наиболее простыми являются детерминированный (когда условия, в которых принимается решение, известны полностью) и стохастический (когда известно множество возможных вариантов условий и их вероятностное распределение). В этих случаях задача сводится к нахождению экстремума функции (или ее математического ожидания).

Наиболее сложной является ситуация неопределенности, т.е. ситуация, когда известно множество возможных вариантов, но без какой-либо информации об их вероятностях.

Теория игр – это теория математических моделей принятия решений в условиях неопределенности. В этих условиях принимающий решение субъект (игрок) располагает информацией о множестве возможных ситуаций, о множестве решений (стратегий), которые он может принять, и о количественной мере того выигрыша, который он мог бы получить, выбрав в данной ситуации данную стратегию.

Неопределенность, с которой мы встречаемся в теории игр, может иметь различное происхождение. Однако, как правило, она является следствием сознательной деятельности другого лица (лиц), отстаивающего свои интересы. В связи с этим под теорией игр часто понимают теорию математических моделей принятия оптимальных решений в условиях конфликта. Таким образом, моделями теории игр можно в принципе содержательно описывать весьма разнообразные явления: экономические, правовые и классовые конфликты, взаимодействие человека с природой, биологическую борьбу за существование и т.д. Все такие модели в теории игр принято называть играми.

Математическое описание игры сводится к перечислению всех действующих в ней игроков, указанию для каждого игрока всех его стратегий, а также численного выигрыша, который он получит после того, как игроки выберут свои стратегии. В результате игра становится формальным объектом, который поддается математическому анализу.

Основные определения теории игр

Рассмотрим основные элементы и понятия теории игр.

Игра – совокупность правил, определяющих количество участников игры, их возможные действия и распределение выигрышей в зависимости от их поведения и исходов.

Игрок – одна из сторон в игровой ситуации. Игроком принято считать одного участника или группу участников игры, имеющих одни общие для них интересы, не совпадающие с интересами других групп. Поэтому не каждый участник считается игроком. Так, например, если в игре принимают участие четыре человека, и каждый играет только за себя, то в ней имеется четыре игрока, если же четыре человека образовали две коалиции по два участника в каждой, т.е. играют двое на двое, то считается, что в этой игре участвуют два игрока.

Пример 1

Пусть три фирмы, имеющие определенный капитал, хотят использовать его для получения возможности сбыта своей продукции на рынке. Каждая из этих фирм, вкладывая капитал, может сбывать свою продукцию с некоторой выгодой для себя. Эта выгода зависит не только от вклада одной фирмы, а от вкладов, сделанных другими фирмами. Ни одна из фирм не имеет полного влияния на рынок сбыта, т.е. каждая фирма только частично влияет на конечный результат – выгоду, получаемую ею. Рассматривая экономическую ситуацию, возникшую в результате взаимодействия трех фирм, как игру, можно допустить:

1) все три фирмы действуют самостоятельно, добиваясь наибольшей выгоды для себя за счет своих возможностей и учитывая возможные поведения других фирм, тогда это будет игра трех игроков;

2) какие-либо две фирмы объединились в коалицию и действуют совместно с единой целью достигнуть наибольшей выгоды для себя, учитывая возможные поведения третьей фирмы, тогда это будет игра двух игроков.

Пример 2

Две войсковых части, имеющие войсковые подразделения, желают овладеть определенной позицией. Первая часть имеет два подразделения, а вторая – три. Возможные действия частей – это выделение определенного количества подразделений для овладения позицией.

Каждое подразделение может иметь свои локальные цели, но все подразделения одной части имеют одну общую цель – овладение позицией. Поэтому, рассматривая сложившуюся ситуацию как игру, следует считать, что в ней имеется только два игрока – это войсковые части.

Ход – выбор игроком одного из предусмотренных правилами игры действий. Сделать ход – это значит, на определенном этапе игры осуществить сразу весь выбор или его часть в зависимости от возможностей, предусмотренных правилами игры. Каждый игрок на определенном этапе игры делает ход согласно сделанному выбору. Другой игрок, зная или не зная о сделанном выборе первого игрока, также делает ход. Каждый из игроков старается учесть информацию о прошлом развитии игры, если такая возможность разрешается правилами игры.

Ходы бывают личные и случайные. Личный ход – сознательный выбор игроком одного из возможных вариантов действия и его осуществление. случайный ход – выбор, осуществляемый не волевым решением игрока, а каким-либо механизмом случайного выбора (монета, кубик, карты и т.п.)

Партия – определенная совокупность ходов и выборов возможных вариантов действий.

Стратегия – набор правил, которые однозначно указывают игроку, какой выбор он должен сделать при каждом ходе в зависимости от ситуации, сложившейся в результате проведения игры. Стратегия в теории игр означает определенный законченный план действий игрока, показывающий, как надо действовать ему во всех возможных случаях развития игры. Стратегия означает совокупность всех указаний для любого состояния информации, имеющейся у игрока на любом этапе развития игры. Отсюда уже видно, что стратегии могут быть хорошими и плохими, удачными и неудачными и т.д.

При игре в шахматы стратегия должна указывать игроку, какой ход он должен сделать в любом развитии игры. Очевидно, при таком подходе в шахматной игре имеется очень много стратегий, перечислить которые практически не представляется возможным и поэтому при анализе и изучении стратегий в этой игре выделяют главные и ими пользуются. Для разных игроков главными являются разные стратегии, как правило, известные только самому игроку, и поэтому игра в шахматы представляет интеллектуальный интерес, несмотря на то, что в ней нет случайных ходов.

При игре в футбол также имеется очень много стратегий и каждая команда применяет свой набор стратегий для того, чтобы достигнуть цели. В этой игре, конечно, большую роль играет и мастерство, которое также может входить в состав стратегии команд и игроков. В играх, отображающих экономические ситуации, стратегиями могут быть размеры вкладываемых в определенные мероприятия средств. Так, в игре трех фирм каждая из них может внести определенную долю своего капитала – это и есть ее стратегия. Очевидно, таких стратегий у каждой фирмы много. В военных играх в качестве стратегий может быть любое поведение подразделений.

Правилами игры предусматриваются определенные выигрыши для игроков в зависимости от применяемых ими стратегий и исходов игры.

Под выигрышем или платежом подразумевается полезность, которую получает игрок, после того как все игроки выбрали свои стратегии. Выигрыш или проигрыш сторон оценивается численно, другие случаи в теории не рассматриваются. Выигрыш – это мера эффекта для игрока. Он может выражаться в денежных суммах, очках, баллах и т.п. Так, в покере, преферансе и других играх после игры обычно происходит обмен ценностями в виде денег, т.е. эффект от исхода этих игр измеряется в денежных единицах. В правилах игры четко сформулировано, сколько денег выиграет каждый игрок в зависимости от исхода игры.

В таких играх, как шашки, шахматы, исходом игры является выигрыш, ничья, проигрыш. Выигрыши здесь измеряются очками (выигрыш – одно очко, ничья – половина очка, проигрыш – нуль очков). При игре в футбол результат игры измеряется очками: выигрыш – два очка, ничья – одно очко, проигрыш – нуль очков. В играх, отображающих экономические ситуации, выигрыши почти всегда измеряются в стоимостном выражении: прибыль, себестоимость, амортизация и т. д. Так, в описанной выше ситуации трех фирм выигрыш может измеряться той прибылью, которую получит фирма в результате применения стратегий всеми фирмами. В военных играх выигрыш – это победа, взятие позиции, получение определенных преимуществ, получение оружия и т. д.

Бывают реальные ситуации, в которых выигрыш оценивается как чувство удовольствия или морального удовлетворения, а проигрыш как чувство угнетения. Так что не всякий выигрыш может измеряться количественно. В теории игр рассматриваются только такие игры, в которых выигрыш выражается количественно: стоимостью, очками, баллами и т. д. Очевидно, исход игры, а следовательно, и выигрыш игроков зависят от стратегий, которые применяют игроки. Однако выигрыш каждого игрока не полностью зависит от применяемой им стратегии, он зависит и от стратегий, применяемых другими игроками.

В конечном счете, в игре никакой игрок не может полностью контролировать свой выигрыш. Если же в реальной ситуации возникает случай, когда исход для участника полностью зависит от него, то такая ситуация не рассматривается для него как игровая. В дальнейшем будут рассматриваться выигрыши, измеряемые количественно (числами). Проигрыш выражается как отрицательный выигрыш. Поэтому речь в дальнейшем будет идти только о выигрышах.

Исход игры в узком смысле понимается как множество платежей.

Равновесием в игре называется комбинация стратегий игроков, которые являются наилучшими ответами на стратегии друг друга.

Стратегией равновесия игрока называется «наилучшая» стратегия, которая дает ему наибольший выигрыш при условии, что другие игроки выбрали свои стратегии.

Игра – математическая модель конфликтной ситуации.

Для того чтобы решить игру, следует для каждого игрока выбрать стратегию, которая удовлетворяет условию оптимальности, т.е. один из игроков должен получать максимальный выигрыш, когда второй придерживается своей стратегии. В то же время второй игрок должен иметь минимальный проигрыш, если первый игрок придерживается своей стратегии.

Классификация игр

Реальные конфликтные ситуации приводят к различным видам игр. В зависимости от вида игры разрабатывается и метод ее решения.

Различные виды игр можно классифицировать, основываясь на том или ином принципе: по количеству игроков, количеству стратегий, характеру взаимодействия игроков, характеру выигрыша, количеству ходов, состоянию информации и т.д.

В зависимости от количества игроков различают игры двух и n игроков. Первые из них наиболее изучены. Игры трех и более игроков менее исследованы из-за возникающих принципиальных трудностей и технических возможностей получения решения. Чем больше игроков – тем больше проблем.

Примеры: игра одного лица (пасьянс), игра двух лиц (шахматы) и т.д.

По количеству стратегий игры делятся на конечные и бесконечные. Конечная игра имеет конечное число ходов, каждый из которых содержит лишь конечное число возможных стратегий. В противном случае игра называется бесконечной.

По характеру взаимоотношений игры делятся на: бескоалиционные, кооперативные и коалиционные.

Бескоалиционными называются игры, в которых игроки не имеют права вступать в соглашения, образовывать коалиции. Например, бескоалиционной будет военная ситуация, в которой сражение ведется без компромиссов, до победы.

Коалиционной игрой называется игра, в которой игроки могут вступать в соглашения, образовывать коалиции. Например, коалиционной будет военная игра (ситуация), в которой противники могут вступать в переговоры с целью достижения компромиссного решения в возникшей ситуации.

В кооперативной игре коалиции наперед определены.

По характеру выигрышей игры делятся на: игры с нулевой суммой и игры с ненулевой суммой.

Игра называется игрой с нулевой суммой, если сумма выигрышей всех игроков равна нулю (т.е. каждый игрок выигрывает только за счет проигрыша других).

Рассмотрим партию с игроками Р₁, Р₂, …, Р _n и р _i (i = 1, …, n) – платежи i-му игроку в конце партии (если Р _i платит сам, то p_i – отрицательно).

Если правила таковы, что 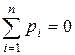, то партия называется партией с нулевой суммой. Если любая возможная партия некоторой игры имеет нулевую сумму, то игра называется игрой с нулевой суммой

Игра двух лиц с нулевой суммой называется антагонистической, так как цели игроков в ней прямо противоположные: выигрыш одного игрока происходит только за счет проигрыша другого.

Антагонистические игры, в которых оба игрока имеют конечные множества стратегий, называются матричными.

Примером игры с ненулевой суммой могут быть торговые взаимоотношения между странами. В результате применения своих стратегий все страны могут быть в выигрыше. Всякая игра, в которой надо вносить взнос некоторому лицу за право принимать участие в ней, является игрой с ненулевой суммой. Действительно, в этом случае всегда в выигрыше получается некоторое лицо, которое не принимает участия в игре, а получает взнос от игроков, теряющих свой капитал за счет этих взносов. Другим примером служит лотерея: в ней организатор всегда имеет выигрыш, а участники игры –лица, купившие лотерейные билеты, – в сумме получают выигрыш меньше, чем они внесли.

По виду функций выигрыша игры делятся на: матричные, биматричные, непрерывные, выпуклые, сепарабельные, типа дуэлей и др.

Матричная игра – это конечная игра двух игроков с нулевой суммой, в которой задаются выигрыши первого игрока в виде матрицы (строка матрицы соответствует номеру применяемой стратегии первого игрока, столбец – номеру применяемой стратегии второго игрока; на пересечении строки и столбца матрицы находится выигрыш первого игрока, соответствующий применяемым стратегиям). Выигрыш второго игрока равен проигрышу первого

Для матричных игр доказано, что любая из них имеет решение, и оно может быть легко найдено путем сведения игры к задаче линейного программирования.

Биматричная игра – это конечная игра двух игроков с ненулевой суммой, в которой выигрыши каждого игрока задаются матрицами отдельно для соответствующего игрока (в каждой матрице строка соответствует стратегии первого игрока, столбец – стратегии второго игрока, на пересечении строки и столбца в первой матрице находится выигрыш первого игрока, во второй матрице – выигрыш второго игрока).

Для биматричных игр также разработана теория оптимального поведения игроков, однако решать такие игры сложнее, чем обычные матричные.

Непрерывной считается игра, в которой функция выигрышей каждого игрока является непрерывной в зависимости от стратегий. Доказано, что игры этого класса имеют решения, однако не разработано практически приемлемых методов их нахождения. Простым примером непрерывной игры двух игроков является следующая: первый игрок выбирает число х из отрезка [0, 1], и второй игрок выбирает число у из отрезка [0, 1], после чего первый игрок выигрывает х – у², а второй проигрывает столько же. Очевидно функция х – у² является непрерывной и поэтому игра также считается непрерывной. Согласно теореме существования решения такая игра имеет решение.

Если функция выигрышей является выпуклой, то такая игра называется выпуклой. Для них разработаны приемлемые методы решения, состоящие в отыскании чистой оптимальной стратегии (определенного числа) для одного игрока и вероятностей применения чистых оптимальных стратегий другого игрока. Такая задача решается сравнительно легко.

Если функция выигрышей может быть представлена в виде суммы произведений функций от одного аргумента, то такая игра называется сепарабельной (разделимой). С помощью определенных преобразований ее решение сводится к решению игры с билинейной функцией выигрышей и к определению неподвижной точки при специальном отображении множеств элементов, соответствующих стратегиям.

Игры типа дуэлей характеризуются моментом выбора хода и вероятностями получения выигрышей в зависимости от времени, прошедшего от начала игры до момента выбора. Например, существуют интерпретации таких игр в экономических ситуациях: каждая фирма делает вклад своего капитала в определенный момент времени с целью овладения рынком сбыта. Чем раньше она сделает свой вклад, тем меньшая вероятность овладеть рынком, но, делая свой вклад слишком поздно, она теряет рынок сбыта. Функция выигрышей игроков в играх типа дуэлей принимает специальный вид: она непрерывна при разных значениях моментов времени, когда игроки делают ходы, и она разрывна при совпадении моментов хода игроков. Так что нет гарантий существования решений для игр типа дуэлей. Существуют определенные методы решения таких игр.

По количеству ходов игры делятся на одношаговые и многошаговые. Одношаговые (статические) игры заканчиваются после одного хода каждого игрока. Например, матричная игра является одношаговой, так как при этом каждый игрок делает только один ход и потом происходит распределение выигрышей.

Многошаговые (динамические) игры делятся на позиционные, стохастические, дифференциальные, типа дуэлей и др.

В позиционных играх может быть несколько игроков, каждый из которых может последовательно во времени делать несколько ходов. Выигрыши определяются в зависимости от исходов игры (применяемых стратегий). Такие игры с помощью определенных способов сводятся к матричным играм и могут решаться присущими им методами.

Если в игре производятся ходы, приводящие к выбору определенных позиций, причем имеется определенная вероятность возврата на предшествующую позицию, то такая игра является стохастической.

Если в многошаговой игре допускается делать ходы непрерывно и подчинять поведение игроков некоторым условиям, описываемым дифференциальными уравнениями, то такие игры являются дифференциальными. Например, в играх типа погони каждый объект может двигаться, подчиняясь определенным условиям, описываемым обыкновенными дифференциальными уравнениями. Цель одного объекта – достичь определенной области, цель другого – не допустить первого до этой области. Выигрыш оценивается определенным числом (функцией).

В зависимости от состояния информации различают игры с полной информацией и с неполной информацией. Если на каждом ходе игры каждому игроку известно, какие выборы были сделаны игроками раньше, то это игра с полной информацией.

Примерами таких игр являются шашки, шахматы. Если в игре не все известно о предыдущих выборах, то это игра с неполной информацией.

Доказано, что всякая игра с полной информацией имеет решение в виде седловой точки в чистых стратегиях. Например, для игры в шахматы это значит, что для каждого игрока имеется такая стратегия, придерживаясь которой, игрок либо выигрывает, либо сведет партию в ничью. Сложность заключается в отыскании такой стратегии. Существуют и другие виды игр, которые здесь не рассматриваются. Возможны и некоторые другие принципы классификации игр.

Игра одного игрока с нулевой суммой не представляет никаких проблем, поскольку, что бы игрок ни делал, он получает ноль. Поэтому он может выбирать любой ход.

При игре одного лица с ненулевой суммой игроку нужно решить обычную задачу на max: он должен выбрать из различных, имеющихся у него альтернатив ту, которая дает ему max выигрыш.

Матричные антагонистические игры

Будем рассматривать игры двух лиц с нулевой суммой, в которой каждый игрок имеет лишь один ход. Каждый игрок делает по одному ходу, затем один игрок платит другому сумму, которая зависит от выборов, сделанных двумя игроками.

Матричная игра двух игроков с нулевой суммой может рассматриваться как следующая абстрактная игра двух игроков.

Первый игрок имеет m стратегий i = 1, 2, ..., m, второй имеет n стратегий j = 1, 2, ..., n. Каждой паре стратегий (i, j) поставлено в соответствие число a_ij, выражающее выигрыш первого игрока за счет второго игрока, если первый игрок применит свою i-ю стратегию, а второй – свою j-ю стратегию.

Каждый из игроков делает один ход: первый игрок выбирает свою i-ю стратегию (i =1, 2, …, m), второй – свою j-ю стратегию (j = 1, 2, ..., n), после чего первый игрок получает выигрыш a_ij за счет второго игрока (если a_ij, < 0, то это значит, что первый игрок платит второму сумму | a_ij |). На этом игра заканчивается.

Каждая стратегия игрока i = 1, 2, …, m; j = 1, 2, ..., n часто называется чистой стратегией.

Матричная игра двух игроков с нулевой суммой далее будет называться просто матричной игрой. Очевидно, матричная игра относится к антагонистическим играм. Из ее определения следует, что для задания матричной игры достаточно задать матрицу А = (a_ij) порядка m ´ n выигрышей первого игрока.

Данная игра записывается в виде матрицы выигрыша первого игрока. Строка матрицы соответствует номеру применяемой стратегии первого игрока, столбец – номеру применяемой стратегии второго игрока; на пересечении строки и столбца матрицы находится выигрыш первого игрока, соответствующий применяемым стратегиям. Элементы a_ij – значение функции выигрыша первого игрока в ситуации, когда первый игрок выбрал свою i-ю стратегию, а второй игрок – свою j-ю стратегию. Для второго игрока в этом случае a_ij – проигрыш.

А =	а₁₁	…	a_1j	…	а₁_n
	…	…	…	…	…
	a_i₁	…	a_ij	…	a_in
	…	…	…	…	…
	a_m₁	…	a_mj	…	a_mn

Такие игры называются прямоугольными.

Для формализации реальной конфликтной ситуации в виде матричной игры надо выделить и перенумеровать чистые стратегии каждого игрока и составить матрицу выигрышей.

Следующий этап – это определение оптимальных стратегий и выигрышей игроков.

Примеры прямоугольной игры

Пример 1.

А = {1, 2, 3}

В = {1, 2, 3, 4}

		1	2	3	4
А	1	2	1	10	11
	2	0	–1	–1	2
	3	–3	–5	–1	1

В платит А сумму, указанную в матрице. (платежная матрица)

Если А выбирает 1 стратегию, а В – 2 стратегию, то В платит А 1 руб.

Если А выбирает 3 стратегию, а В – 1 стратегию, то А платит В 3 руб.

Пример 2. Двухпальцевая Морра.

Играют 2 человека: Каждый показывает один или два пальца и одновременно называет число пальцев, которые, по его мнению, покажет другой игрок (противник). Если один из игроков указывает правильно, он выигрывает сумму, равную сумме пальцев, показанных им и его противником, в противном случае – ничья.

Составить платежную матрицу.

Очевидно, в этой игре каждый из имеющихся двух участников игры является игроком, так как у них противоположные интересы: получить выигрыш за счет другого участника игры. Поэтому рассматриваемая игра принадлежит к игре двух игроков с нулевой суммой.

Обозначим m – количество пальцев, показанных игроком, n – количество пальцев, угаданных игроком.

Платежная матрица

А В	(1,1)	(1,2)	(2,1)	(2,2)
(1,1)	0 (оба угадали)	2	–3	0
(1,2)	–2 (угадал Р₂)	0	0	3
(2,1)	3 (угадал Р₁)	0	0	–4
(2,2)	0 (никто не угадал)	–3	4	0

Пример 3.

Два игрока играют в следующую игру. Независимо друг от друга они кладут на стол монету в 1 и 2 руб. Если монеты одинакового достоинства, то выигрывает игрок А, если разного – игрок В. Сумма выигрыша в обоих случаях равна сумме достоинства монет. Построить платежную матрицу игры.

Итак, в этой конфликтной ситуации принимают участие только два человека, у которых прямо противоположные цели – получить максимальный выигрыш за счет второго участника, поэтому каждого участника следует считать игроком. Отсюда следует, что формализованная игра будет игрой двух игроков с нулевой суммой.

Стратегии игрока А: А₁ – положить 1 руб.; А₂ – положить 2 руб.

Стратегии игрока В: В₁ – положить 1 руб.; В₂ – положить 2 руб.

	В₁ (1 руб.)	В₂ (2 руб.)
А₁ (1 руб.)	2	–3
А₂ (2 руб.)	–3	4

Важнейшим вопросом в случае прямоугольной игры, да и вообще любой игры является вопрос о том, имеется ли оптимальный способ игры, т.е. можно ли доказать, что данный способ игры является наиболее рациональным.

В случае первого примера на этот вопрос ответить легко. Каждый элемент первой строки больше соответствующего элемента 2-й и 3-й строк, следовательно, какой бы выбор ни сделал В, А лучше выбрать 1.

Каждый элемент второго столбца меньше соответствующих элементов 1, 3 и 4 столбцов. Поэтому, чтобы проигрыш В был как можно меньше, оптимальный способ игры для него – выбрать 2.

Прямоугольные игры с седловыми точками.

Дата добавления: 2021-04-05; просмотров: 211; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 4 5 Следующая ⇒

Мы поможем в написании ваших работ!