Применение дифференциального исчисления для исследования функции одной переменной. Исследование функции с помощью второй производной.
Асимптоты графика функции.
Выпуклость и вогнутость кривой.

|
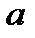
|
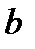
|
|
|
|
Определение.
1) Кривая называется выпуклой (выпуклой вверх) на интервале 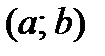 , если все точки кривой расположены ниже любой ее касательной на этом интервале.
, если все точки кривой расположены ниже любой ее касательной на этом интервале.
2) Кривая называется вогнутой (выпуклой вниз) на интервале 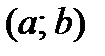 , если все точки кривой расположены выше любой ее касательной на этом интервале.
, если все точки кривой расположены выше любой ее касательной на этом интервале.
Теорема (достаточное условие выпуклости, вогнутости кривой).
1) Если функция дважды дифференцируема на интервале 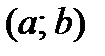 и во всех точках этого интервала
и во всех точках этого интервала 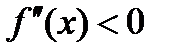 , то кривая
, то кривая  выпукла вверх при
выпукла вверх при 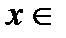
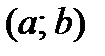 .
.
2) Если во всех точках этого интервала 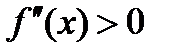 , то кривая
, то кривая  вогнута на этом интервале.
вогнута на этом интервале.
Определение. Точкой перегиба кривой  называется точка, отделяющая выпуклую часть непрерывной кривой от вогнутой.
называется точка, отделяющая выпуклую часть непрерывной кривой от вогнутой.
Очевидно, что в точках перегиба касательная пересекает кривую, т.к. по одну сторону точки кривая лежит ниже касательной, а по другую – над ней.
Приведем достаточное условие существования точки перегиба.
Теорема 6. Пусть кривая задана уравнением  . Тогда если
. Тогда если 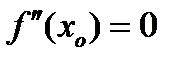 или
или  не существует, и при переходе через точку
не существует, и при переходе через точку  вторая производная меняет знак, то точка с координатами
вторая производная меняет знак, то точка с координатами 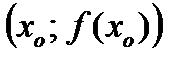 является точкой перегиба.
является точкой перегиба.
Замечание. Внутренние точки из области определения функции, в которых 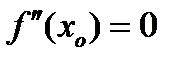 или
или  не существует, называются критическими точками II рода.
не существует, называются критическими точками II рода.
|
|
|
Асимптоты кривой.
Определение. Прямая называется асимптотой кривой  , если расстояние от точки кривой до этой прямой стремится к нулю при бесконечном удалении точки от начала координат.
, если расстояние от точки кривой до этой прямой стремится к нулю при бесконечном удалении точки от начала координат.
Различают вертикальные и наклонные асимптоты.
|
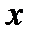
|
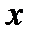
|
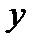
|
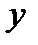
|
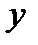
|

|

|

|

|
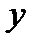
|
|
| Горизонтальная асимптота является частным случаем наклонной. |
1) Вертикальные асимптоты.
Уравнение вертикальной асимптоты 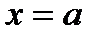 . Для существования вертикальной асимптоты необходимо и достаточно, чтобы хотя бы один из пределов
. Для существования вертикальной асимптоты необходимо и достаточно, чтобы хотя бы один из пределов 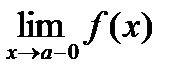 ;
; 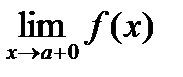 был равен бесконечности.
был равен бесконечности.
2) Наклонные асимптоты.
В общем виде уравнение наклонной асимптоты можно записать в виде уравнения прямой 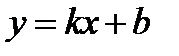 . Различают правую и левую наклонную асимптоты.
. Различают правую и левую наклонную асимптоты.
а) Правая наклонная асимптота: если при 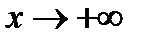
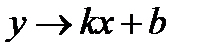 , то
, то 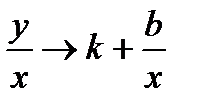 .
.
Но при 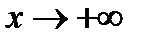 имеем
имеем 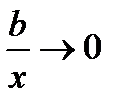 . Следовательно,
. Следовательно, 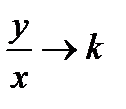 , т.е.
, т.е. 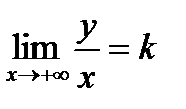 , или
, или 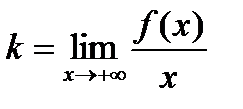 .
.
После нахождения 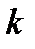 (в случае его существования) находят
(в случае его существования) находят 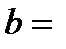
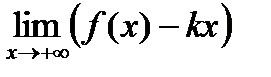 .
.
Итак, схема нахождения правой наклонной асимптоты 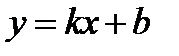 : сначала вычисляют
: сначала вычисляют
|
|
|
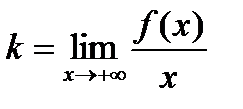 . Если этот предел существует (конечный), то вычисляют
. Если этот предел существует (конечный), то вычисляют 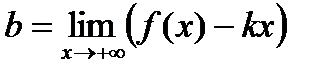 . Если и этот предел существует (конечный), то уравнение правой наклонной асимптоты
. Если и этот предел существует (конечный), то уравнение правой наклонной асимптоты 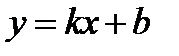 .
.
Если хотя бы один из пределов  ;
;  не существует (конечный), то правой наклонной асимптоты нет. В случае
не существует (конечный), то правой наклонной асимптоты нет. В случае  получаем горизонтальную асимптоту, уравнение которой
получаем горизонтальную асимптоту, уравнение которой 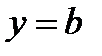 , где
, где  .
.
б) Уравнение левой наклонной асимптоты 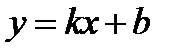 ,
, 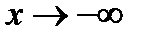 , находится аналогично:
, находится аналогично:
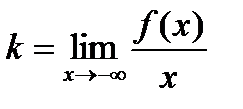 ;
; 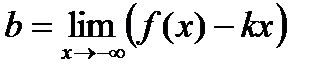 .
.
Правило Лопиталя.
Это правило используется для устранения неопределенностей вида 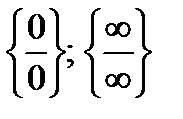
при вычислении пределов вида 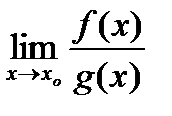 ,
, 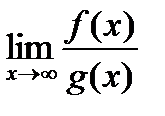 .
.
Сформулируем правило Лопиталя для случая неопределенности 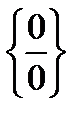 .
.
Теорема. Пусть 1) 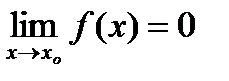 ;
; 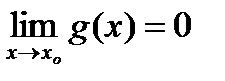 ;
;
2) 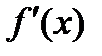 и
и 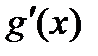 существуют в некоторой проколотой окрестности точки
существуют в некоторой проколотой окрестности точки 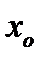 , и пусть
, и пусть  в этой окрестности.
в этой окрестности.
Тогда, если существует конечный или бесконечный предел  ,
,
то 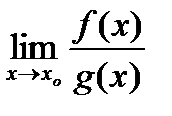
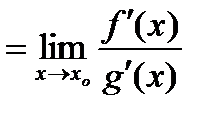 .
.
Примеры.
1) 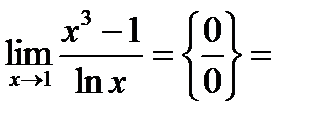
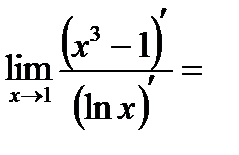
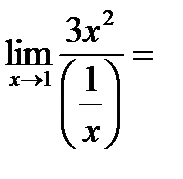
 .
.
Функции 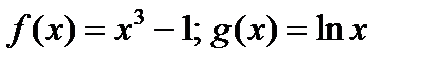 дифференцируемые,
дифференцируемые, 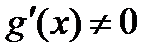 в некоторой проколотой окрестности точки
в некоторой проколотой окрестности точки  . Поэтому правило Лопиталя применять можно.
. Поэтому правило Лопиталя применять можно.
2) 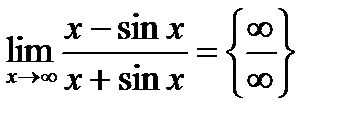 .
.
Правило Лопиталя применять нельзя, т.к. 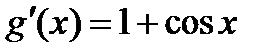 обращается в ноль в любой окрестности
обращается в ноль в любой окрестности  (т.е. при
(т.е. при 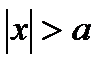 ).
).
Общая схема исследования функции и построения графика.
|
|
|
При исследовании поведения функции  и построении ее графика целесообразно придерживаться следующей схемы.
и построении ее графика целесообразно придерживаться следующей схемы.
1. Найти область определения функции, исследовать 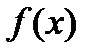 на непрерывность.
на непрерывность.
2. Исследование 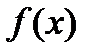 на четность.
на четность.
3. Исследование 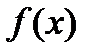 на периодичность.
на периодичность.
4. Нахождение точек пересечения графика функции с осями координат, нахождение интервалов знакопостоянства 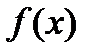 (методом интервалов).
(методом интервалов).
5. Исследование поведения функции вблизи точек разрыва и на границах области определения (т.е. вычисление односторонних пределов). Нахождение вертикальных асимптот.
6. Нахождение наклонных асимптот.
7. Исследование по 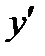 (на возрастание, убывание, нахождение экстремумов).
(на возрастание, убывание, нахождение экстремумов).
8. Исследование по 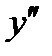 (на выпуклость, вогнутость, нахождение точек перегиба).
(на выпуклость, вогнутость, нахождение точек перегиба).
Полученные знания следует постепенно наносить на чертеж.
Пример.
Построить график функции 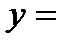
 . Решение.
. Решение.
1) Область определения функции: 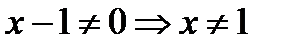 .
.  является точкой разрыва.
является точкой разрыва.
2) Так как область определения не симметрична оси OX, то функция общего вида.
3) Функция не является периодической.
4) Точки пересечения с осью OX: 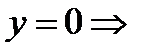
 =0
=0 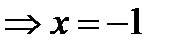 ;
; 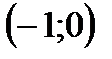 .
.
Точка пересечения с осью OY:  .
.
|
|
|
Интервалы знакопостоянства:
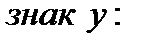
|

|
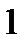
|
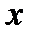
|
5) Исследование поведения функции вблизи точек разрыва и на границах ОДЗ:
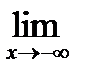
 =
= 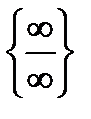 =
= 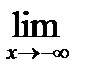
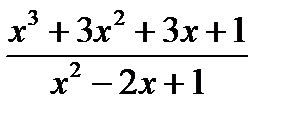 =
= 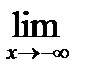
 =
= 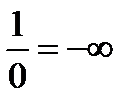 .
.
Знак «-» соответствует исследованному знаку 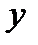 .
.

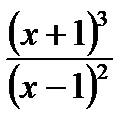 =
=  =
= 
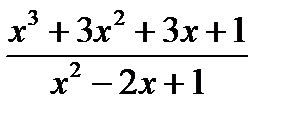 =
= 
 =
= 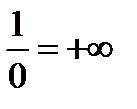 .
.

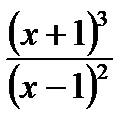 =
= 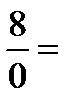

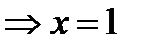 является вертикальной асимптотой.
является вертикальной асимптотой.
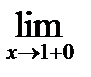
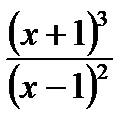 =
= 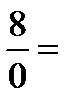
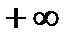 .
.
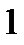
|

|
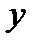
|
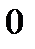
|
| Вычисленные пределы изображаем на графике. |
6) Находим наклонные асимптоты.
а) Правая наклонная асимптота 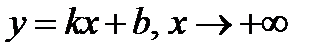 .
.
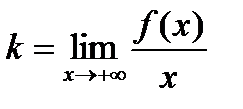 =
= 
 =
= 
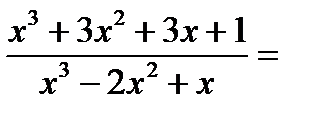

 1.
1.
 =
= 
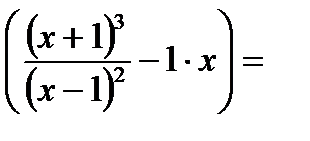


 =
=
= 
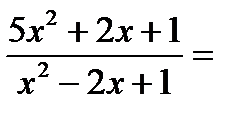

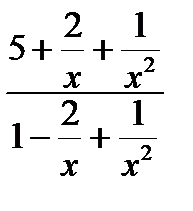 =5. Подставляя найденные
=5. Подставляя найденные 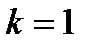 и
и  в уравнение
в уравнение 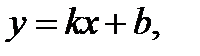 получаем уравнение правой наклонной асимптоты:
получаем уравнение правой наклонной асимптоты: 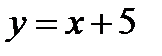 .
.
б) Левая наклонная асимптота 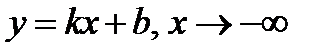 в данном примере та же
в данном примере та же 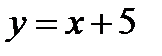 , так как при вычислении
, так как при вычислении 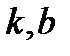 в предыдущем пункте нигде не использовался знак «плюс» бесконечности. Следовательно,
в предыдущем пункте нигде не использовался знак «плюс» бесконечности. Следовательно, 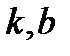 при
при 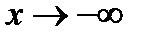 будут такими же.
будут такими же.
Вывод: 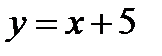 - двусторонняя наклонная асимптота.
- двусторонняя наклонная асимптота.
Отмечаем на графике:
|
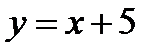
|

|

|

|
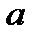
|
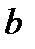
|

|
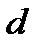
|
При 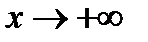 график приближается к асимптоте график приближается к асимптоте 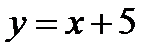 либо сверху ( либо сверху (  ), либо снизу ( ), либо снизу ( 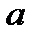 ). Аналогично и для ). Аналогично и для 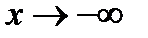 . Какой из случаев имеет место, будет известно после исследования на выпуклость. . Какой из случаев имеет место, будет известно после исследования на выпуклость.
|
7) Исследование по 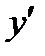 (на возрастание, убывание, нахождение экстремумов).
(на возрастание, убывание, нахождение экстремумов).
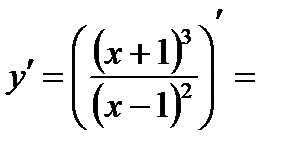
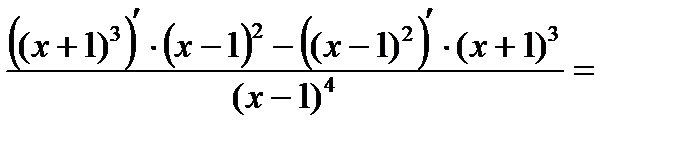
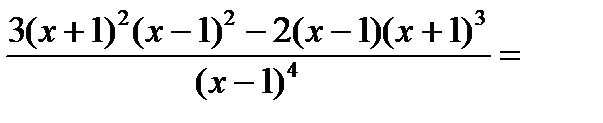

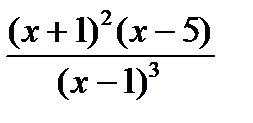 . Заметим, что вычисленную производную следует разлагать на множители. В этом виде удобно находить критические точки и исследовать знак.
. Заметим, что вычисленную производную следует разлагать на множители. В этом виде удобно находить критические точки и исследовать знак.
Ищем критические точки: 
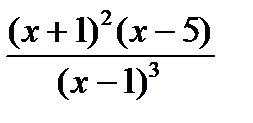 =0
=0 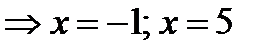 . Эти точки являются внутренними точками ОДЗ, следовательно, являются критическими точками
. Эти точки являются внутренними точками ОДЗ, следовательно, являются критическими точками
I рода. 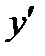 не существует при
не существует при 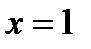 , но эта точка не принадлежит ОДЗ, поэтому критической не является. Итак, получены критические точки I рода:
, но эта точка не принадлежит ОДЗ, поэтому критической не является. Итак, получены критические точки I рода: 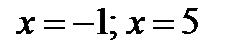 .
.
Это точки возможного экстремума. Проверим по достаточному условию. Для этого исследуем знак 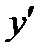 :
:
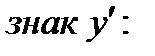
|

|

|

|

|
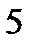
|
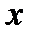
|
При переходе через точку 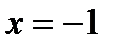
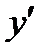 не меняет знака, поэтому эта точка не является точкой экстремума. Однако в этой точке касательная к графику параллельна оси OX.
не меняет знака, поэтому эта точка не является точкой экстремума. Однако в этой точке касательная к графику параллельна оси OX.
При переходе через 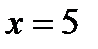 производная менякт знак с «-» на «+», следовательно, является точкой минимума. Вычисляем значения функции в критических точках:
производная менякт знак с «-» на «+», следовательно, является точкой минимума. Вычисляем значения функции в критических точках:
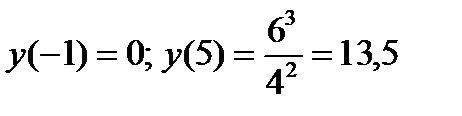 .
.
Отмечаем на графике:
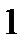
|
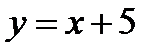
|

|

|

|
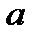
|
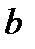
|

|
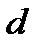
|
При 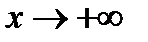 график приближается к асимптоте график приближается к асимптоте 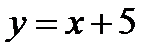 либо сверху ( либо сверху (  ), либо снизу ( ), либо снизу ( 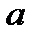 ). Аналогично и для ). Аналогично и для 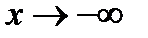 . Какой из случаев имеет место, будет известно после исследования на выпуклость. . Какой из случаев имеет место, будет известно после исследования на выпуклость.
|
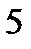
|
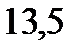
|
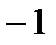
|
8) Исследование по 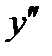 (на выпуклость, вогнутость, нахождение точек перегиба).
(на выпуклость, вогнутость, нахождение точек перегиба).
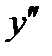 =
= 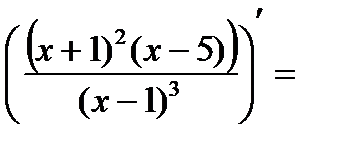
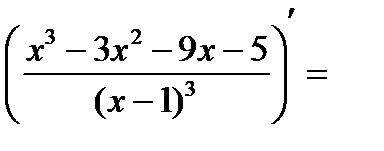
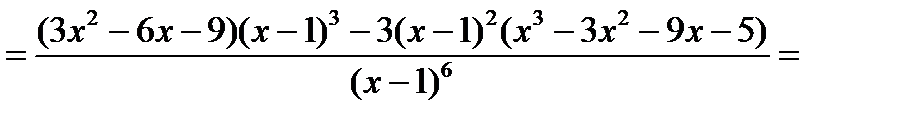

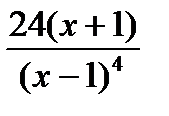 .
.
Ищем критические точки II рода: 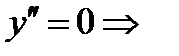
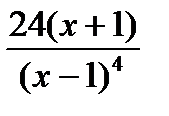 =0
=0 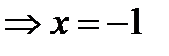 является критической, т.к. принадлежит ОДЗ.
является критической, т.к. принадлежит ОДЗ. 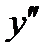 не существует при
не существует при 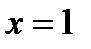 , но эта точка не принадлежит ОДЗ, поэтому критической не является. Итак, получена критическая точки II рода:
, но эта точка не принадлежит ОДЗ, поэтому критической не является. Итак, получена критическая точки II рода: 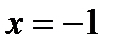 .
.
Исследуем знак 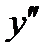 :
:
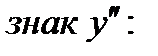
|

|

|
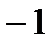
|
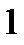
|
При переходе через точку 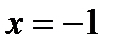
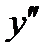 меняет знак
меняет знак 
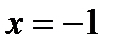 является точкой перегиба.
является точкой перегиба.
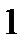
|
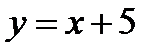
|

|

|

|
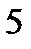
|
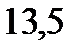
|
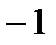
|
Теперь можно определить, какой из вариантов подхода к асимптоте имеет место. Так как при 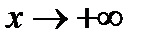 кривая вогнута, то выбираем кривая вогнута, то выбираем 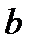 ; при ; при 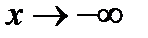 кривая выпукла вверх кривая выпукла вверх  выбираем выбираем  . Теперь строим график. . Теперь строим график.
|
Дата добавления: 2021-04-23; просмотров: 66; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
