Производная сложной и обратной функции.
Теорема. Пусть функции 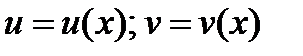 имеют производные в точке
имеют производные в точке  . Тогда справедливы соотношения:
. Тогда справедливы соотношения:
1) 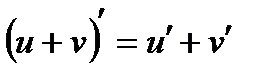 (1)
(1)
2) 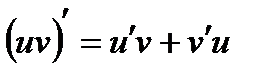 (2)
(2)
3) 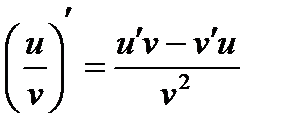 . (3)
. (3)
Доказательство. Придадим аргументу 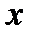 приращение
приращение  . Тогда функция
. Тогда функция 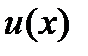 получит приращение
получит приращение 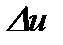 ,
, 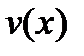 получит приращение
получит приращение  . Так как по условию теоремы
. Так как по условию теоремы 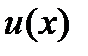 и
и 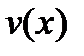 имеют производные, то по теореме из предыдущего пункта эти функции непрерывны в точке
имеют производные, то по теореме из предыдущего пункта эти функции непрерывны в точке 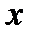 . Следовательно, при
. Следовательно, при 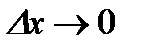 имеют место:
имеют место: 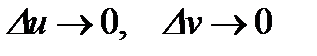 .
.
1) Если 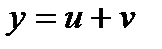 , то
, то 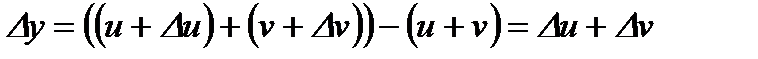 ;
;


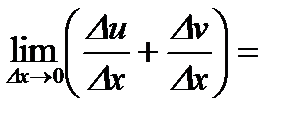
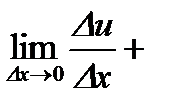

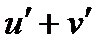 .
.
2) Если 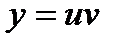 , то
, то  ;
;


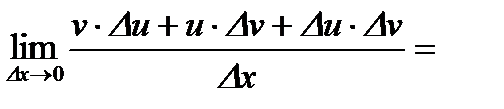
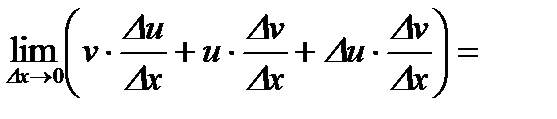
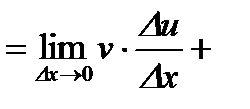
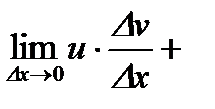
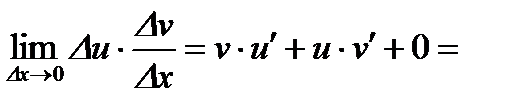
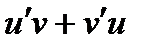 .
.
Из теоремы вытекает следствие: если  , то
, то  . (4)
. (4)
Доказательство. Сначала найдем производную для функции 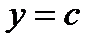 , где
, где  .
.
Если 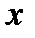 получило приращение
получило приращение  , то
, то 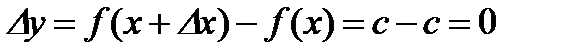 . Следовательно,
. Следовательно, 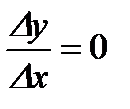 , тогда
, тогда 
 0. Таким образом,
0. Таким образом, 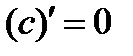 .
.
Тогда, подставляя в (2)  , где
, где  , с учетом
, с учетом 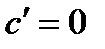 , получим (4).
, получим (4).
Соотношения (1)-(4) называют правилами дифференцирования.
Пример. Найдем производную для 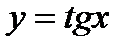 .
.
 . Тогда, используя (3), получаем:
. Тогда, используя (3), получаем: 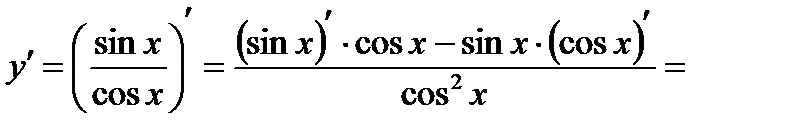
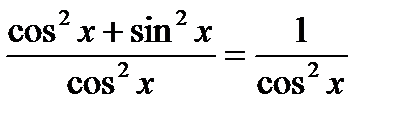 .
.
Таким образом, 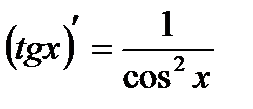 .Аналогично доказывается
.Аналогично доказывается 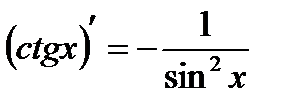 .
.
Производная сложной функции.
Пусть задана сложная функция 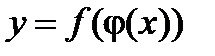 .
.
Теорема. Если функция 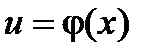 имеет производную
имеет производную  в точке
в точке  , а функция
, а функция  имеет производную
имеет производную 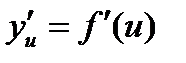 в соответствующей точке
в соответствующей точке 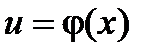 , то и сложная функция
, то и сложная функция 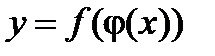 имеет производную в точке
имеет производную в точке  . При этом
. При этом 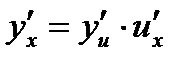 .
.
Примеры. Найти производные функций:
1) 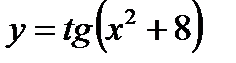 - сложная функция. Обозначим:
- сложная функция. Обозначим:  .
.

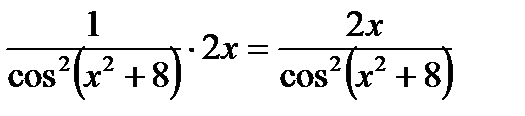 .
.
2) 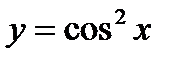 - сложная функция. Обозначим
- сложная функция. Обозначим 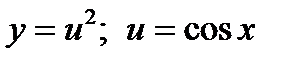 .
.
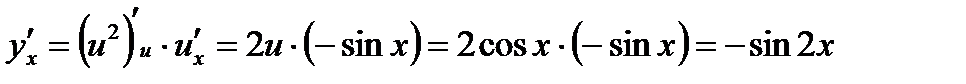 .
.
3) 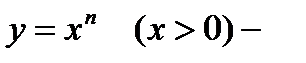 простая функция. Однако для нахождения
простая функция. Однако для нахождения 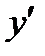 представим ее в виде сложной:
представим ее в виде сложной:
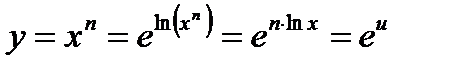 , где
, где  .
.
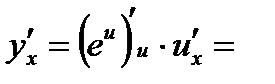
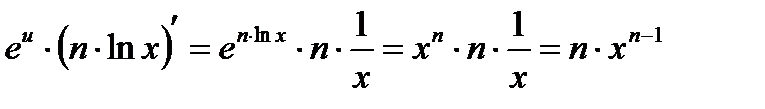 .Таким образом,
.Таким образом, 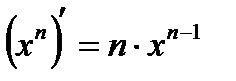 .
.
Можно доказать, что это соотношение справедливо для любых 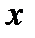 , при которых функция
, при которых функция
|
|
|
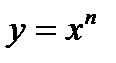 определена.
определена.
Производная обратной функции.
Рассмотрим функцию  , возрастающую (убывающую) и непрерывную на некотором промежутке
, возрастающую (убывающую) и непрерывную на некотором промежутке 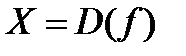 . Тогда по теореме существования для этой функции существует обратная функция
. Тогда по теореме существования для этой функции существует обратная функция 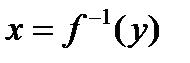 , определенная в соответствующем промежутке
, определенная в соответствующем промежутке 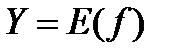 , также возрастающая (убывающая) и непрерывная.
, также возрастающая (убывающая) и непрерывная.
Теорема. Пусть  - монотонная, непрерывная функция, определенная на промежутке
- монотонная, непрерывная функция, определенная на промежутке  и имеющая в точке
и имеющая в точке 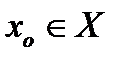 производную, отличную от нуля:
производную, отличную от нуля:  . Тогда обратная функция
. Тогда обратная функция 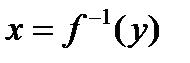 в соответствующей точке
в соответствующей точке 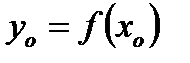 имеет производную
имеет производную 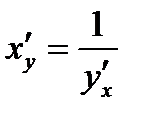 .
.
Пример. Найти производную функции  .
.
Решение. Функция, обратная заданной, имеет вид 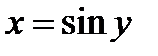 . Тогда
. Тогда
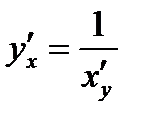
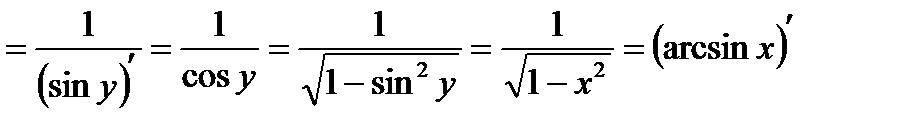 .
.
Преобразования выполнены с учетом того, что для  , поэтому
, поэтому 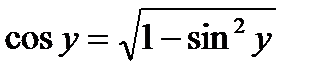 .
.
Аналогично доказываются следующие формулы:
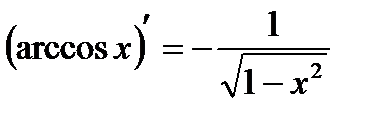 ;
; 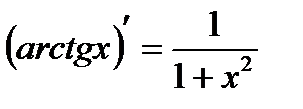 ;
;  .
.
Объединим в одну таблицу основные формулы и правила дифференцирования.
Таблица производных.
1)  , где
, где  .
.
2)  , где
, где 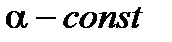 . В частности,
. В частности,  .
.
3) 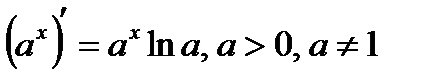 .
.
В частности, 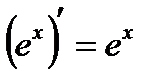 .
.
4) 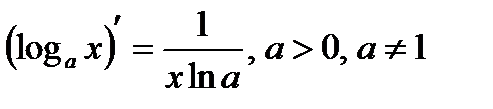 . В частности,
. В частности,  .
.
5) 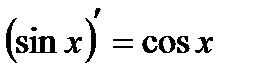 . 6)
. 6)  .
.
7) 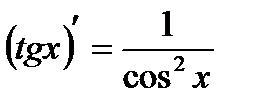 . 8)
. 8) 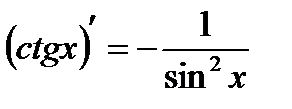 .
.
9) 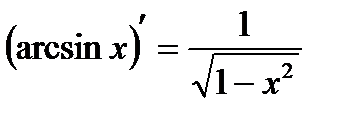 . 10)
. 10) 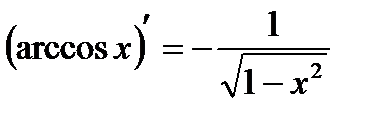 .
.
11) 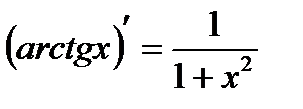 . 12)
. 12) 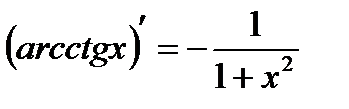 .
.
Правила дифференцирования.
I. Если 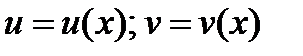 - дифференцируемые функции,
- дифференцируемые функции, 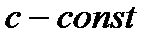 , то
, то
|
|
|
1) 
2) 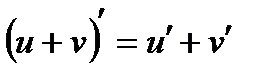
3) 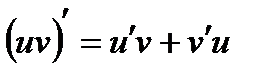
4) 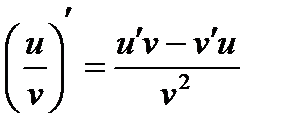 .
.
Лекция 3.
Дифференциал функции одной переменной. Геометрический смысл дифференциала. Инвариантность формы первого дифференциала.
Теоремы Ферма, Ролля, Лагранжа, Коши.
Дифференциал функции. Связь дифференциала с производной.
Пусть функция  определена в некоторой окрестности точки
определена в некоторой окрестности точки 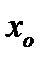 и непрерывна
и непрерывна
при 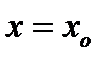 . Пусть
. Пусть 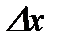 - приращение независимой переменной в этой точке. Если приращение функции
- приращение независимой переменной в этой точке. Если приращение функции  в точке
в точке 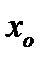 можно представить в виде
можно представить в виде
 , (1)
, (1)
где 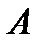 не зависит от
не зависит от 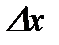 , а
, а 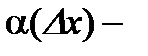 б/м при
б/м при 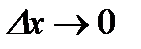 , то функцию
, то функцию  называют дифференцируемой в точке
называют дифференцируемой в точке 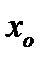 .
.
Пример. Пусть 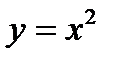 . Тогда, выбрав произвольное
. Тогда, выбрав произвольное 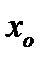 , получаем:
, получаем:
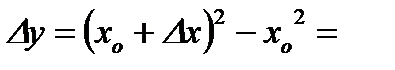
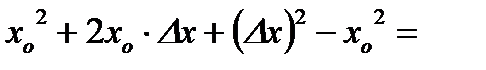
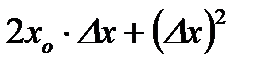 .
.
Обозначив  (
(  не зависит от
не зависит от 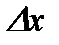 ),
),  , получаем, что для функции
, получаем, что для функции 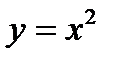
в точке 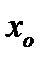
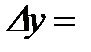
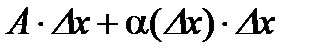 . Заметим, что в данном примере
. Заметим, что в данном примере 
 .
.
Определение. Дифференциалом функции  называется главная часть ее приращения
называется главная часть ее приращения 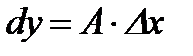 , линейная относительно приращения независимой переменной
, линейная относительно приращения независимой переменной 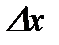 .
.
Теорема. Для того, чтобы функция  была дифференцируема в точке
была дифференцируема в точке 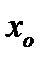 , необходимо и достаточно, чтобы в этой точке существовала конечная производная
, необходимо и достаточно, чтобы в этой точке существовала конечная производная 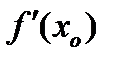 , при этом
, при этом 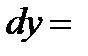
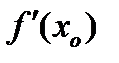
 . (2)
. (2)
|
|
|
Доказательство.
1) Необходимость. Пусть функция  дифференцируема в точке
дифференцируема в точке 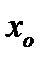 , т.е.
, т.е. 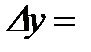
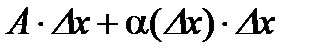 . Тогда, разделив обе части равенства на
. Тогда, разделив обе части равенства на 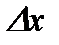 и переходя к пределу
и переходя к пределу
при 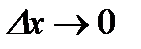 , получаем
, получаем 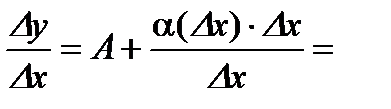
 ;
;
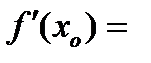

 .
.
Таким образом, из дифференцируемости функции в точке следует существование производной и равенство 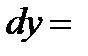
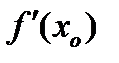
 .
.
2) Достаточность. Пусть для функции  в точке
в точке 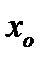 существует производная
существует производная 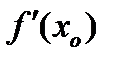 . Тогда
. Тогда 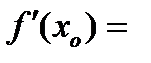
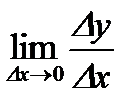 , или
, или 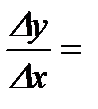
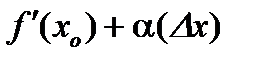 , где
, где 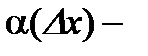 б/м при
б/м при 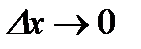 .
.
Умножив обе части этого равенства на 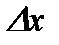 , получим
, получим 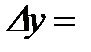
 . (3)
. (3)
Так как 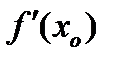 не зависит от
не зависит от 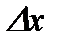 , и
, и 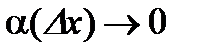 при
при 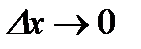 , то равенство (3)
, то равенство (3)
аналогично (1). При этом 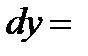
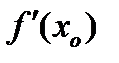
 .
.
Замечание.
1) Из определения и теоремы вытекает, что для всякой дифференцируемой в точке 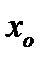 функции справедливо соотношение
функции справедливо соотношение 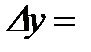
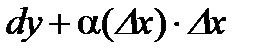 . Тогда
. Тогда  , (4)
, (4)
поскольку 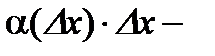 б/м более высокого порядка, чем
б/м более высокого порядка, чем 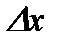 .Это равенство широко применяют для приближенных вычислений.
.Это равенство широко применяют для приближенных вычислений.
2) Введем понятие дифференциала независимой переменной. Для этого рассмотрим функцию  . С одной стороны,
. С одной стороны,  . С другой стороны, из теоремы следует, что
. С другой стороны, из теоремы следует, что 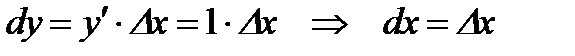 .
.
Таким образом, дифференциал независимой переменной равен приращению этой переменной: 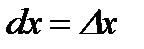 . (5)
. (5)
3) С учетом (5) формулу (2) для вычисления дифференциала функции можно записать в виде 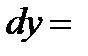

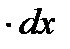 . (6)
. (6)
|
|
|
Из этого равенства вытекает, что  . Следовательно, производная функции
. Следовательно, производная функции  равна отношению дифференциала функции
равна отношению дифференциала функции  к дифференциалу независимой переменной
к дифференциалу независимой переменной 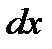 .
.
Геометрический смысл дифференциала..
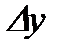
|
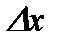
|
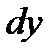
|
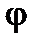
|

|
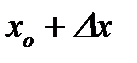
|
|

|
|
|
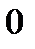
|
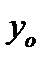
|
Пусть задана функция  , имеющая производную в точке , имеющая производную в точке  . Из существования производной следует, что . Из существования производной следует, что 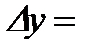 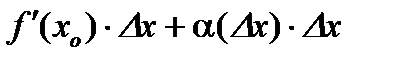 . Тогда . Тогда 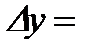 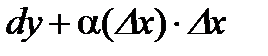 . .
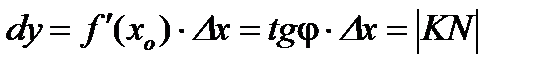 . Следовательно, дифференциал функции равен приращению ординаты касательной . Следовательно, дифференциал функции равен приращению ординаты касательной 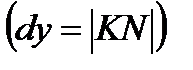 , проведенной к кривой , проведенной к кривой 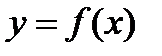
|
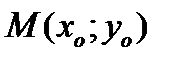 при приращении аргумента
при приращении аргумента 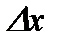 .
.
Свойства дифференциала функции.
Если 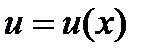 и
и  дифференцируемые функции,
дифференцируемые функции,  , то
, то
1) 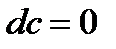 .
.
2)  .
.
3)  .
.
4)  .
.
5)  .
.
6) 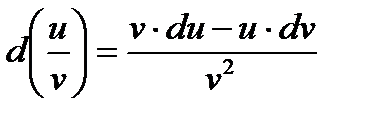 .
.
Доказательство. В качестве примера докажем свойство 5.
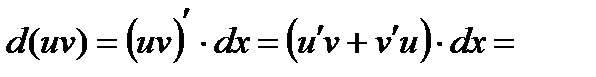

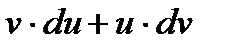 .
.
Остальные свойства доказываются аналогично.
Производные высших порядков.
Как уже ранее отмечалось, если функция 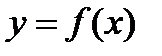 имеет производную
имеет производную  в каждой точке некоторого промежутка
в каждой точке некоторого промежутка  , то сама производная является функцией независимой переменной
, то сама производная является функцией независимой переменной 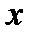 . Если при этом функция
. Если при этом функция  дифференцируема,
дифференцируема,
т.е. существует производная 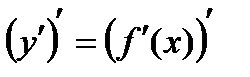 , то ее называют второй производной функции
, то ее называют второй производной функции 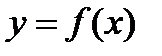 . Рассуждая аналогично, получим
. Рассуждая аналогично, получим 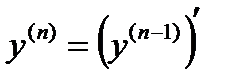 .
.
Определение. Производной  го порядка функции
го порядка функции 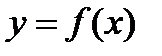 называется производная от производной
называется производная от производной 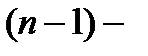 го порядка.
го порядка.
Примеры.
1)  .
.
2) 
Вторая производная 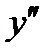 от функции
от функции 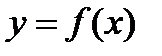 имеет определенный физический смысл. Если
имеет определенный физический смысл. Если 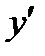 характеризует скорость изменения переменной
характеризует скорость изменения переменной 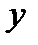 , то величина
, то величина  задает ускорение.
задает ускорение.
Основные теоремы дифференциального исчисления.
Дифференциальное исчисление является удобным аппаратом для исследования функций. В основе различных приложений лежат рассматриваемые ниже теоремы, которые также называют теоремами о среднем.
Теорема Ферма.
Теорема. Если функция 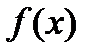 определена на некотором промежутке
определена на некотором промежутке  , во внутренней точке
, во внутренней точке 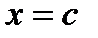 этого промежутка принимает наибольшее (наименьшее) значение, и в этой точке существует конечная производная
этого промежутка принимает наибольшее (наименьшее) значение, и в этой точке существует конечная производная 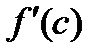 , то
, то 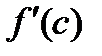
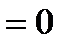 .
.
Доказательство. Положим, для определенности, что в точке  функция
функция 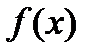 принимает наибольшее значение:
принимает наибольшее значение: 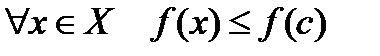 , тогда при любом
, тогда при любом 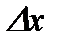
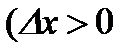 или
или  получим:
получим:
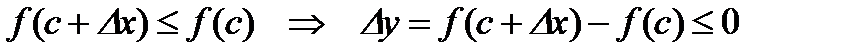 . Следовательно, при
. Следовательно, при 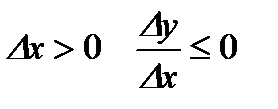 ,
,
а при 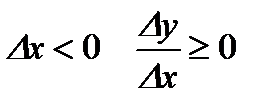 . Поскольку, по условию теоремы, производная при
. Поскольку, по условию теоремы, производная при 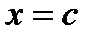 существует, то, перейдя к пределу в неравенствах при
существует, то, перейдя к пределу в неравенствах при 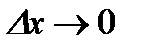 , получаем:
, получаем:
при 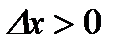

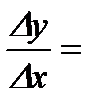
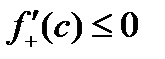 ; при
; при 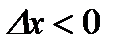
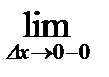
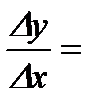
 .
.
Существование производной обусловливает тот факт, что левая и правая производные должны быть равны, а это возможно лишь в том случае, когда 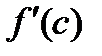
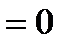 . Таким образом, из существования производной
. Таким образом, из существования производной 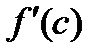 следует:
следует: 

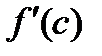
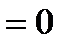 .
.

|
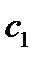
|
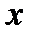
|
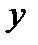
|
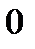
|
Теорема имеет простое геометрическое содержание, а именно: если в точке  функция принимает наибольшее (наименьшее) значение и существует функция принимает наибольшее (наименьшее) значение и существует 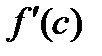 , то , то 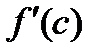 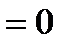 ,следовательно, в этой точке угловой коэффициент касательной ,следовательно, в этой точке угловой коэффициент касательной 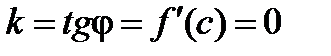 . Тогда . Тогда 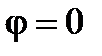
|
 касательная в этой точке параллельна оси OX.
касательная в этой точке параллельна оси OX.
Теорема Ролля.
Теорема. Если функция 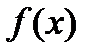 непрерывна на отрезке
непрерывна на отрезке  , дифференцируема на
, дифференцируема на
интервале  и
и 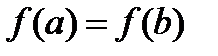 , то существует по крайней мере одна точка
, то существует по крайней мере одна точка 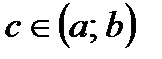 , такая, что
, такая, что 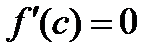 .
.
Доказательство. Так как функция определена и непрерывна на отрезке  , то она принимает на этом промежутке свои наибольшее
, то она принимает на этом промежутке свои наибольшее 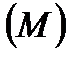 и наименьшее
и наименьшее  значения. При этом возможны следующие случаи:
значения. При этом возможны следующие случаи:
1) 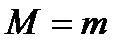 . Тогда функция на всем отрезке – величина постоянная, т.е.
. Тогда функция на всем отрезке – величина постоянная, т.е. 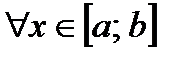
 . Следовательно,
. Следовательно,  , и в качестве точки
, и в качестве точки  можно выбрать любую точку, принадлежащую интервалу
можно выбрать любую точку, принадлежащую интервалу  .
.
2) 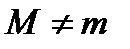 . Тогда
. Тогда  . Причем, поскольку из условия теоремы
. Причем, поскольку из условия теоремы 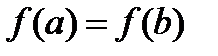 , то хотя бы одно из значений
, то хотя бы одно из значений 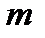 или
или  функция принимает во внутренней точке промежутка
функция принимает во внутренней точке промежутка 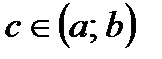 . Тогда, по теореме Ферма, получаем:
. Тогда, по теореме Ферма, получаем: 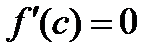 . Теорема доказана.
. Теорема доказана.

|
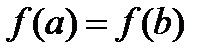
|
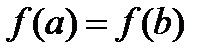
|

|

|

|
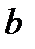
|
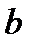
|
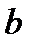
|

|

|
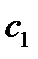
|
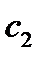
|
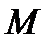
|
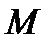
|
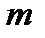
|
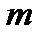
|
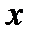
|

|

|

|

|

|
|
|
|
Геометрический смысл заключается в том, что при выполнении условий теоремы на графике функции 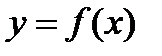 найдется хотя бы одна точка, в которой касательная параллельна оси OX.
найдется хотя бы одна точка, в которой касательная параллельна оси OX.
Заметим, что все условия теоремы существенны, и нарушение хотя бы одного из них делает теорему неверной. В качестве примера можно рассмотреть функцию 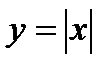
на отрезке  (нарушено условие существования производной во внутренней точке
(нарушено условие существования производной во внутренней точке 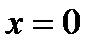 ).
).
Теорема Лагранжа.
Теорема. Если функция 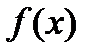 непрерывна на отрезке
непрерывна на отрезке  и дифференцируема на
и дифференцируема на
интервале  , то существует по крайней мере одна точка
, то существует по крайней мере одна точка 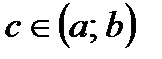 такая, что
такая, что
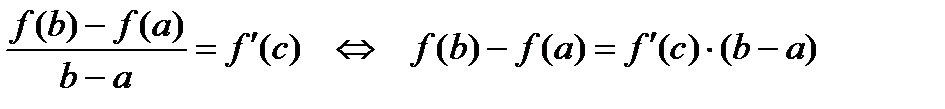 . (1)
. (1)
Соотношение (1) называется формулой Лагранжа.
|

|

|
|
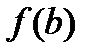
|
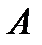
|
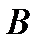
|
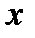
|

|

|
Геометрический смысл теоремы заключается в том, что для функции 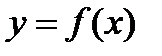 найдется
хотя бы одна точка найдется
хотя бы одна точка 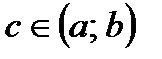 , в которой касательная к графику функции будет параллельна хорде , в которой касательная к графику функции будет параллельна хорде 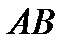 . .
|
Теорема Коши.
Данную теорему называют также теоремой о конечных приращениях.
Теорема. Если функции 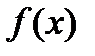 и
и 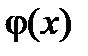 непрерывны на отрезке
непрерывны на отрезке  , дифференцируемы на интервале
, дифференцируемы на интервале  и
и 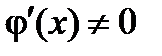 для
для 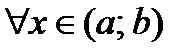 , то существует по крайней мере одна точка
, то существует по крайней мере одна точка 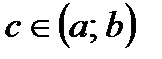 такая, что
такая, что  .
.
Лекция 4.
Дата добавления: 2021-04-23; просмотров: 80; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
