Применение дифференциального исчисления для исследования функции одной переменной. Исследование функции с помощью первой производной.
Условия возрастания и убывания функций.
Напомним, что функция 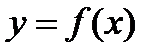 называется возрастающей (убывающей) на интервале
называется возрастающей (убывающей) на интервале  , если
, если  из неравенства
из неравенства 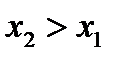 следует неравенство
следует неравенство 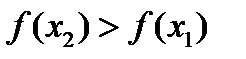
 .
.
Теорема 1 (необходимый признак монотонности).
Пусть функция  дифференцируема на интервале
дифференцируема на интервале  . Тогда:
. Тогда:
1) Если  возрастает на
возрастает на  , то
, то 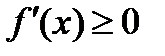 для
для 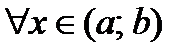 .
.
2) Если  убывает на
убывает на  , то
, то 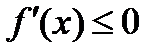 для
для  .
.
3) Если 
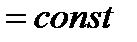 на
на  , то
, то 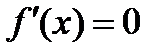 для
для 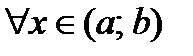 .
.
Доказательство. Пусть  возрастает на
возрастает на  . Придадим аргументу
. Придадим аргументу 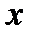 приращение
приращение 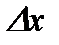 так, что
так, что 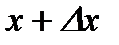 не выходит за пределы интервала
не выходит за пределы интервала  , и рассмотрим отношение
, и рассмотрим отношение 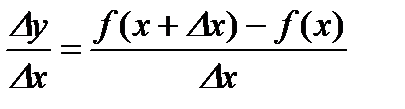 . Так как
. Так как  возрастает на
возрастает на  , то
, то
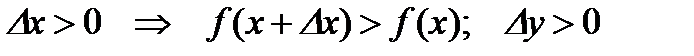 ;
; 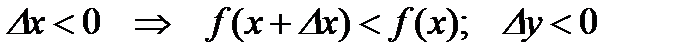 .
.
И в одном, и в другом случае справедливо неравенство 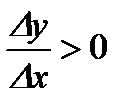 . Переходя к пределу при
. Переходя к пределу при 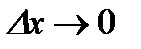 , получаем
, получаем 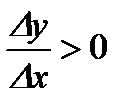

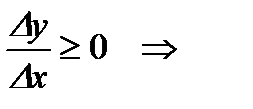
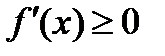 .
.
Доказательство пунктов 2 и 3 аналогично.
Теорема 2 (достаточный признак монотонности).
Пусть функция 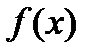 непрерывна на и дифференцируема на интервале
непрерывна на и дифференцируема на интервале  . Тогда
. Тогда
1) Если 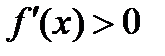 для
для 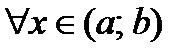 , то
, то  возрастает на
возрастает на  .
.
2) Если 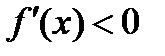 для
для 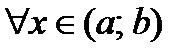 , то
, то  убывает на
убывает на  .
.
3) Если 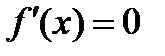 для
для 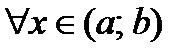 , то
, то 
 на
на  .
.
Доказательство.
1) Рассмотрим случай, когда 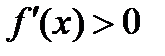 для
для 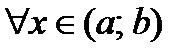 . Выберем произвольные
. Выберем произвольные 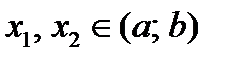 и пусть
и пусть 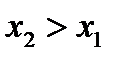 . Заметим, что функция
. Заметим, что функция 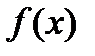 удовлетворяет всем условиям теоремы Лагранжа. Тогда на промежутке
удовлетворяет всем условиям теоремы Лагранжа. Тогда на промежутке 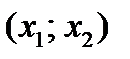 найдется
найдется 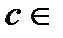
 такая, что
такая, что 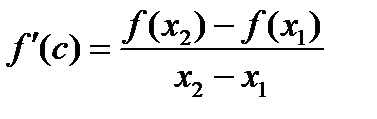 , или
, или  . Так как по условию теоремы
. Так как по условию теоремы  и, кроме того,
и, кроме того, 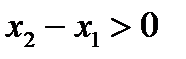 , то получаем, что
, то получаем, что 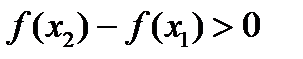 , или
, или  . Следовательно,
. Следовательно,  возрастает на
возрастает на  .
.
Пункты 2 и 3 теоремы доказываются аналогично.
Геометрический смысл теоремы иллюстрирует рисунок:

|
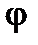
|
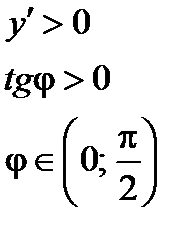
|
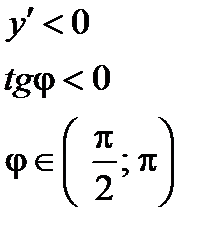
|
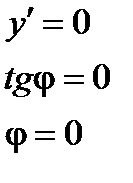
|

|
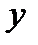
|

|
|
|
|
Локальные экстремумы функции.
Определение.
1) Точка 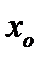 называется точкой локального максимума (
называется точкой локального максимума ( 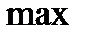 ) функции
) функции 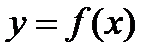 , а число
, а число 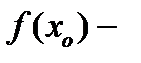 максимумом этой функции, если существует окрестность точки
максимумом этой функции, если существует окрестность точки 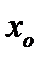 , такая, что для всякого
, такая, что для всякого 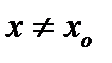 из этой окрестности выполняется неравенство
из этой окрестности выполняется неравенство  .
.
2) Точка 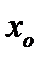 называется точкой локального минимума (
называется точкой локального минимума (  ) функции
) функции 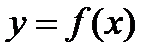 , а число
, а число 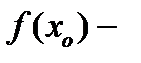 минимумом этой функции, если существует окрестность точки
минимумом этой функции, если существует окрестность точки 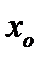 , такая, что для всякого
, такая, что для всякого 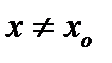 из этой окрестности выполняется неравенство
из этой окрестности выполняется неравенство 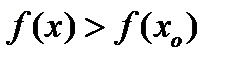 .
.
Точки максимума и минимума функции также называют точками экстремума данной функции. Функция может иметь несколько точек максимума и минимума на каком-либо отрезке.
Теорема 3. Если функция 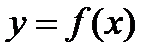 дифференцируема и имеет в точке
дифференцируема и имеет в точке 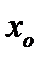 экстремум, то
экстремум, то 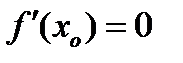 .
.
Доказательство. Пусть в точке 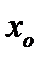 функция достигает максимума. Тогда, согласно определению, существует окрестность точки
функция достигает максимума. Тогда, согласно определению, существует окрестность точки 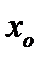 , в которой выполняется неравенство
, в которой выполняется неравенство  . Следовательно,
. Следовательно, 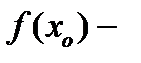 наибольшее значение функции в данной окрестности. Тогда по
наибольшее значение функции в данной окрестности. Тогда по
теореме Ферма 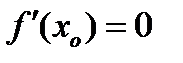 .
.
В случае, когда 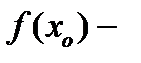 наименьшее значение функции, доказательство аналогично.
наименьшее значение функции, доказательство аналогично.
Замечания.
1) Кроме точек, в которых 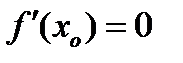 , экстремум может достигаться в точках, где
, экстремум может достигаться в точках, где 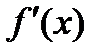 не существует (либо
не существует (либо 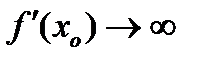 , либо
, либо 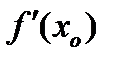 не определена).
не определена).
|
|
|

|
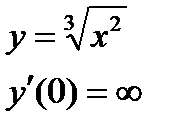
|
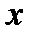
|

|
|
|
|

|
2) Сформулированное в теореме условие является необходимым, но не достаточным, т.е.
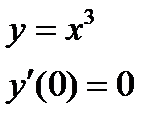
|
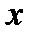
|
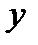
|
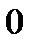
|
равенство нулю производной в точке 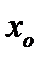 еще не означает, что еще не означает, что 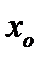 - точка экстремума. Примером может служить функция - точка экстремума. Примером может служить функция 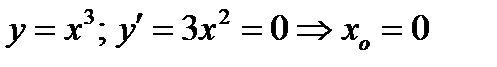 . Но при . Но при 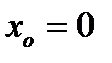 функция функция 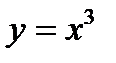 экстремума не имеет. экстремума не имеет.
|
С учетом доказанной теоремы и замечаний сформулируем необходимое условие экстремума:
если 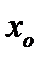 - точка экстремума функции
- точка экстремума функции 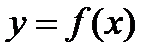 , то
, то 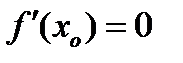 или
или 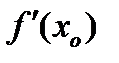 не существует.
не существует.
Определение. Внутренние точки области определения функции, в которых производная равна нулю или не существует, называются критическими точками I рода.
Теорема 4 (первое достаточное условие экстремума).
Пусть функция 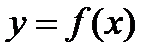 непрерывна в некоторой окрестности критической точки
непрерывна в некоторой окрестности критической точки 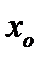 и дифференцируема во всех точках этой окрестности кроме, быть может, самой точки
и дифференцируема во всех точках этой окрестности кроме, быть может, самой точки 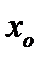 . Тогда если при переходе через точку
. Тогда если при переходе через точку 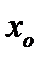 слева направо:
слева направо:
1) производная меняет знак с плюса на минус, то 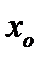 - точка максимума;
- точка максимума;
2) производная меняет знак с минуса на плюс, то 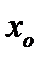 - точка минимума;
- точка минимума;
3) производная не меняет знака, то 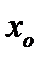 не является точкой экстремума.
не является точкой экстремума.
Геометрический смысл теорем иллюстрирует рисунок.
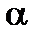
|
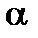
|
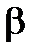
|

|

|

|

|
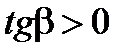
|

|
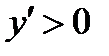
|
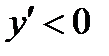
|
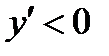
|

|
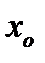
|
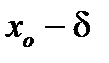
|
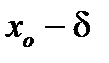
|
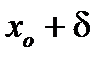
|
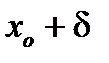
|
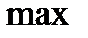
|
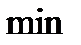
|
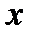
|
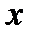
|
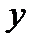
|
|
|
|
|
|
|
При исследовании функций можно также использовать еще один, так называемый второйдостаточный признак экстремума, который мы приведем без доказательства.
Теорема 5. Пусть непрерывная функция 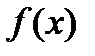 дважды дифференцируема в критической точке
дважды дифференцируема в критической точке  и в некоторой ее окрестности. Тогда
и в некоторой ее окрестности. Тогда
1) если 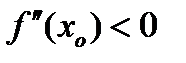 , то
, то 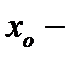 точка максимума функции;
точка максимума функции;
2) если  , то
, то 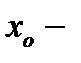 точка минимума функции;
точка минимума функции;
3) если 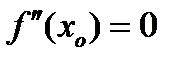 , то необходимо провести дополнительное исследование.
, то необходимо провести дополнительное исследование.
С учетом изложенного, при нахождении точек экстремума функции целесообразно придерживаться следующей схемы:
1) найти производную функции 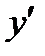 ;
;
2) найти критические точки I рода;
3) используя достаточные условия, проверить каждую критическую точку на существование экстремума.
Лекция 5.
Дата добавления: 2021-04-23; просмотров: 59; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
