Основные правила дифференцирования.
Производная функции. Геометрический и физический смысл производной.
Уравнения касательной и нормали.
Задачи, приводящие к понятию производной.
Задача 1 (о скорости движущейся точки).
| Пусть материальная точка движется неравномерно по прямой. Пройденный точкой |
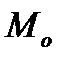
|
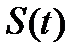
|
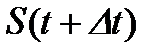
|

|
путь, отсчитываемый от точки 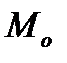 , связан со временем движения законом
, связан со временем движения законом 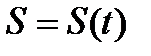 , который известен. За промежуток времени
, который известен. За промежуток времени 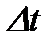 точка проходит путь
точка проходит путь  . Тогда средняя скорость движения точки за период времени от
. Тогда средняя скорость движения точки за период времени от  до
до 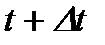 будет
будет 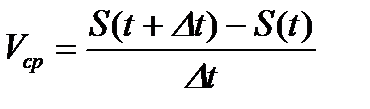 .
.
Мгновенная скорость точки в момент времени  будет равна
будет равна
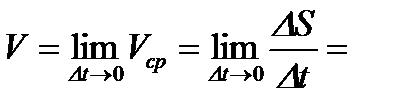
 .
.
Задача 2 (о касательной к данной кривой).

|
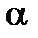
|

|
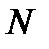
|

|

|
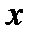
|
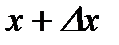
|
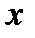
|
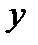
|
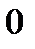
|
|
Пусть задана функция 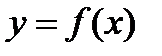 . Возьмем на кривой произвольную точку . Возьмем на кривой произвольную точку  и близкую к ней точку и близкую к ней точку 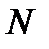 . Прямая . Прямая 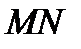 называется секущей. Угол называется секущей. Угол  угол наклона секущей к положительному направлению оси угол наклона секущей к положительному направлению оси 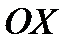 , причем , причем 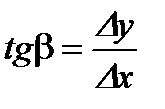 . Будем перемещать точку . Будем перемещать точку 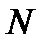 по кривой до совмещения с точкой по кривой до совмещения с точкой 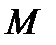 . Тогда предельное . Тогда предельное
|
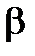
|

|
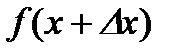
|
положение секущей 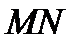 при
при 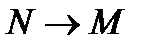 , или
, или 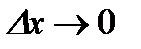 , определит касательную к кривой
, определит касательную к кривой 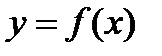 в точке
в точке 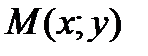 . Причем при
. Причем при 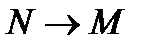 :
: 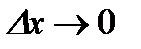 ;
; 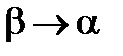 . А так как
. А так как  непрерывная функция в промежутке
непрерывная функция в промежутке 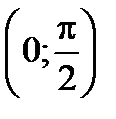 , то
, то 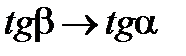 , где
, где  угол наклона касательной к положительному направлению оси
угол наклона касательной к положительному направлению оси 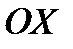 . Величина
. Величина 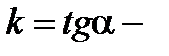 угловой коэффициент касательной. Тогда
угловой коэффициент касательной. Тогда 

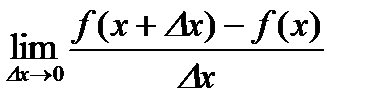 .
.
Во всех рассмотренных задачах, имеющих совершенно различное содержание,
|
|
|
с математической точки зрения вычислялась одна и та же величина, а именно предел приращения функции 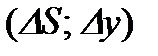 к приращению аргумента
к приращению аргумента 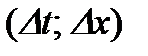 при условии, что приращение аргумента стремится к нулю. Обобщающим понятием для подобных величин является понятие производной.
при условии, что приращение аргумента стремится к нулю. Обобщающим понятием для подобных величин является понятие производной.
Определение. Производной функции 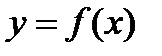 в точке
в точке  называется предел отношения приращения функции
называется предел отношения приращения функции 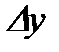 к приращению аргумента
к приращению аргумента  при
при 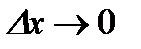 :
:
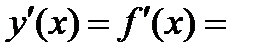

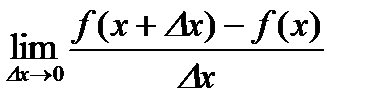 .
.
Определение. Выражения 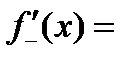
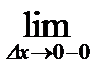
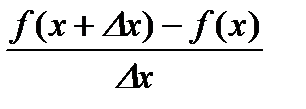 ;
; 
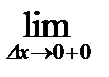
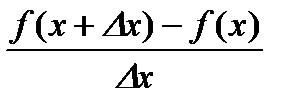 называются соответственно левой и правой производными функциями в точке
называются соответственно левой и правой производными функциями в точке 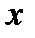 .
.
Для существования производной необходимо и достаточно, чтобы 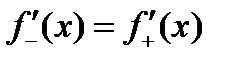 .
.
Физический смысл производной следует из задачи 1. В более широком понимании физический смыл производной заключается в том, что она задает скорость изменения функции.
Геометрический смысл производной следует из задачи 2: величина  равна угловому коэффициенту касательной к графику функции
равна угловому коэффициенту касательной к графику функции 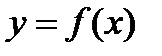 в точке
в точке 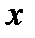 .
.
Примеры.
1) 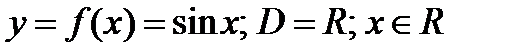 .
.
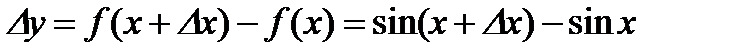 .
.



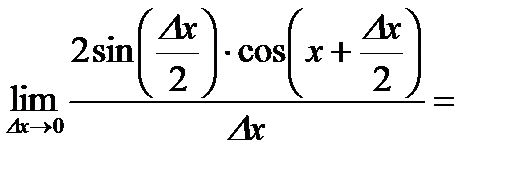
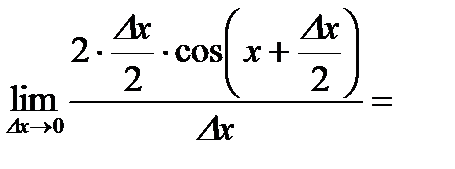
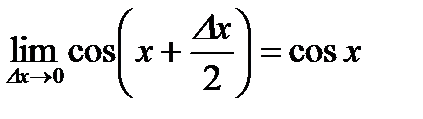
 .
.
Аналогично доказывается  .
.
2) 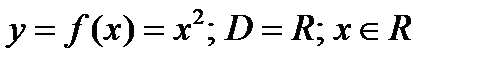 .
.
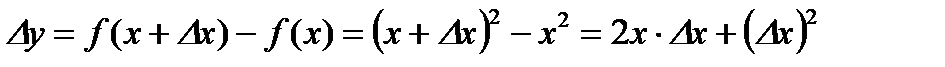 .
.


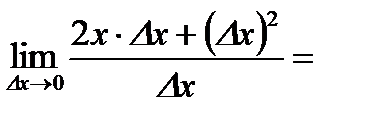

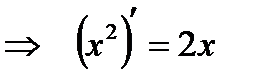 .
.
3)  .
.
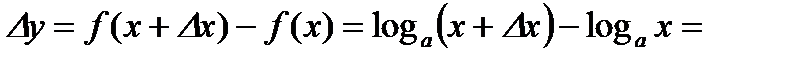
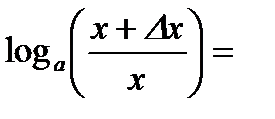
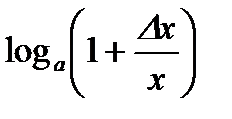 .
.


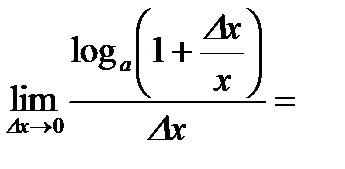
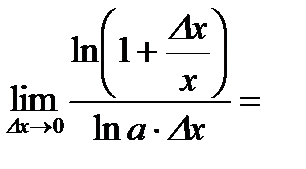
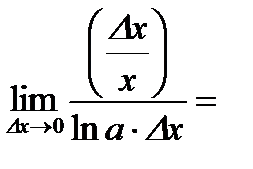
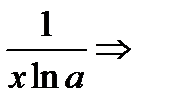
 .
.
В частности, 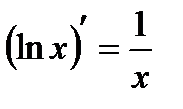 .
.
4) 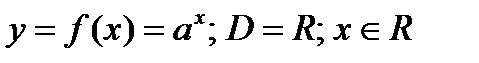 .
.
 .
.


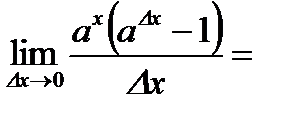
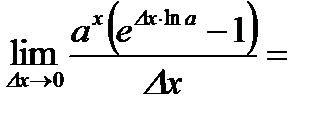
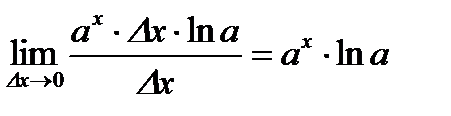
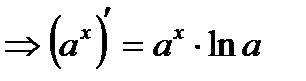 .
.
В частности,  .
.
Уравнения касательной и нормали.
|
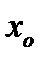
|
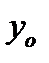
|

|
|

|

|
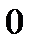
|
Пусть задана кривая 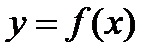 и точка и точка 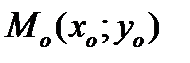 , принадлежащая данной кривой. Пусть также функция , принадлежащая данной кривой. Пусть также функция 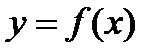 имеет в точке имеет в точке  производную производную 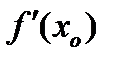 . Найдем уравнение касательной к кривой . Найдем уравнение касательной к кривой  , проходящую через точку , проходящую через точку 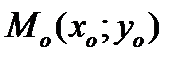 . .
|
|
|
|
Для этого воспользуемся уравнением прямой, проходящей через заданную точку:
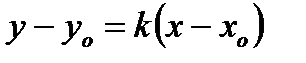 , где
, где  угловой коэффициент прямой.
угловой коэффициент прямой.
Но 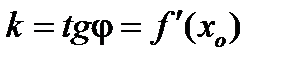 (из геометрического смысла
(из геометрического смысла 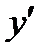 ). Тогда уравнение касательной к кривой
). Тогда уравнение касательной к кривой 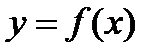 в точке
в точке 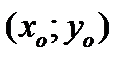 будет
будет  .
.
Нормалью к кривой 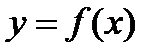 в точке
в точке 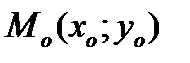 называют прямую, проходящую через
называют прямую, проходящую через
точку 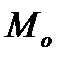 перпендикулярно касательной к кривой в точке
перпендикулярно касательной к кривой в точке 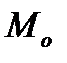 .
.
Как известно, условие перпендикулярности двух прямых: 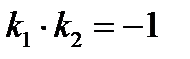 , или
, или 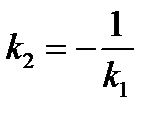 .
.
Следовательно, при условии, что в точке 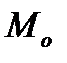
 , уравнение касательной будет
, уравнение касательной будет
 .
.
Непрерывность функции, имеющей производную.
Теорема (необходимое условие существования производной).
Если функция 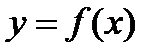 имеет производную в точке
имеет производную в точке  , то она непрерывна в этой точке.
, то она непрерывна в этой точке.
Доказательство. Пусть 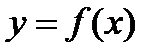 имеет производную в точке
имеет производную в точке  , то есть существует
, то есть существует  .
.
По определению 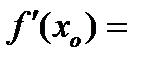

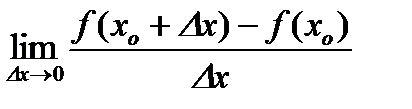 . Тогда по теореме о связи между функцией, ее пределом и бесконечно малой получим
. Тогда по теореме о связи между функцией, ее пределом и бесконечно малой получим 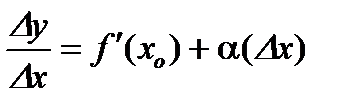 ,
,
где 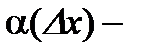 б/м при
б/м при  . Умножив обе части полученного равенства на
. Умножив обе части полученного равенства на 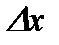 ,
,
получим 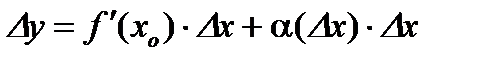 . Тогда
. Тогда 
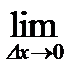

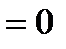 ,
,
что и означает непрерывность функции 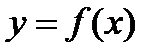 в точке
в точке 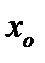 .
.
Таким образом, в точках разрыва функция не может иметь производную.
Замечание. Непрерывность функции является необходимым условием существования производной, но не достаточным. То есть, если функция имеет производную в точке, то она непрерывна. Однако из факта непрерывности функции в точке не обязательно следует, что в этой точке она имеет производную.
|
|
|
Пример. Для иллюстрации сделанного замечания рассмотрим функцию 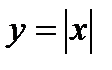 .
.
В точке 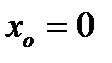 эта функция непрерывна. Найдем левую и правую производные: эта функция непрерывна. Найдем левую и правую производные:
|

|
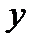
|
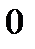
|

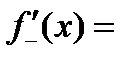
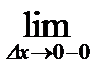
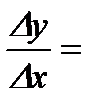
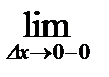
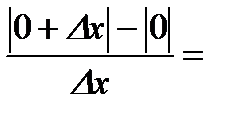
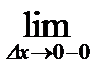
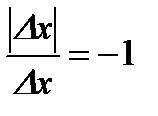 ;
;
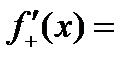
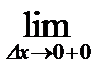
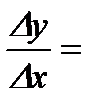

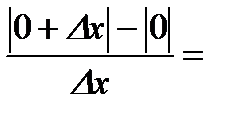
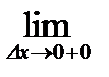
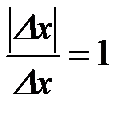 .
.
Так как 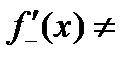
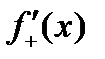 , то производная в этой точке не существует. Геометрически это означает, что в точке
, то производная в этой точке не существует. Геометрически это означает, что в точке 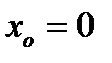 график
график 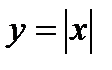 касательной не имеет.
касательной не имеет.
Лекция 2.
Основные правила дифференцирования.
Дата добавления: 2021-04-23; просмотров: 79; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
