Задачи для самостоятельного решения
7. Найти математическое ожидание случайной величины X –количества отказов элемента системы, зная закон ее распределения:
| X | 1 | 5 | 2 |
| p | 0,1 | 0,8 | 0,1 |
8. Производится 3 испытания элемента с вероятностями сохранения работоспособного состояния, равными р1 = 0,2; р2 = 0,3 и р3 =0,5. Найти математическое ожидание общего работоспособного состояния.
9. Вероятность отказа детали за время испытания на надежность равна 0,2. Найти математическое ожидание числа отказавших деталей, если испытанию будут подвергнуты 10 деталей.
10. Независимые случайные величины X и Y заданы следующими законами распределения:
X 5 3 6 Y 5 10
p 0,6 0,1 0,3 p 0,8 0,2
Найти математическое ожидание случайной величины XY.
Распределение случайной величины
Если 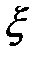 – случайная величина, то функция
– случайная величина, то функция
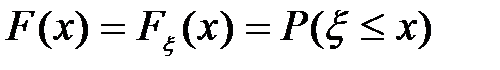 (10)
(10)
называется функцией распределения случайной величины 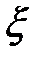 . Здесь −
. Здесь − 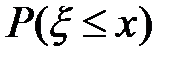 − вероятность того, что случайная величина
− вероятность того, что случайная величина 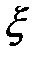 принимает значения, не превосходящие числа
принимает значения, не превосходящие числа 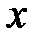 .
.
Функция распределения любой случайной величины обладает следующими свойствами:
· 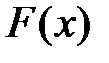 определена на всей числовой прямой R;
определена на всей числовой прямой R;
· 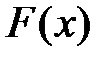 не убывает, т. е. если
не убывает, т. е. если 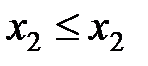 , то
, то 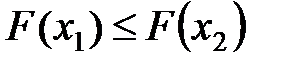 ;
;
· 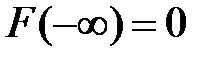 ,
, 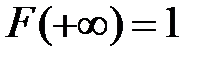 , т. е.
, т. е. 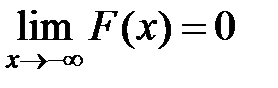 и
и 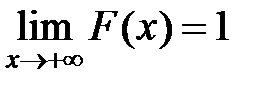
· 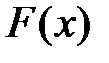 непрерывна справа, т. е.
непрерывна справа, т. е. 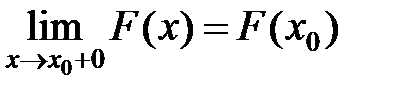 .
.
Функция распределения содержит всю информация об этой случайной величине и поэтому изучение случайной величины заключается в исследовании ее функции распределения, которую часто называют просто распределением. Поэтому, когда говорят о нормальном распределении, то подразумевают случайную величину, имеющую нормальную функцию распределения.
|
|
|
У дискретной случайной величины функция распределения ступенчатая.
Если 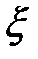 − дискретная случайная величина, принимающая значения
− дискретная случайная величина, принимающая значения 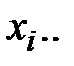
с вероятностями 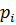 ,то таблица 2.1 называется распределением дискретной случайной величины.
,то таблица 2.1 называется распределением дискретной случайной величины.
Таблица 1 Распределение дискретной случайной величины
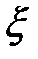
| 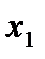
| 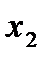
| … | 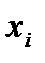
| … |
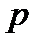
| 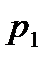
| 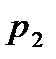
| … | 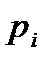
| … |
Биноминальное распределение
Пусть производится n независимых испытаний, в каждом из которых событие А может появиться либо не появиться. Вероятность наступления события во всех испытаниях постоянна и равна p (следовательно, вероятность непоявления 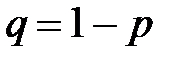 ). Рассмотрим в качестве дискретной случайной величины Х число появлений события А в этих испытаниях.
). Рассмотрим в качестве дискретной случайной величины Х число появлений события А в этих испытаниях.
Поставим перед собой задачу: найти закон распределения величины Х. Для её решения требуется определить возможные значения Х и их вероятности. Очевидно, событие А в n испытаниях либо появится 1 раз, либо 2 раза, …, либо n раз. Таким образом, возможные значения Х таковы: 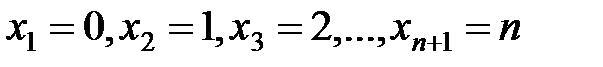 . Остаётся найти вероятности этих возможных значений, для чего достаточно воспользоваться формулой Бернулли:
. Остаётся найти вероятности этих возможных значений, для чего достаточно воспользоваться формулой Бернулли:
|
|
|
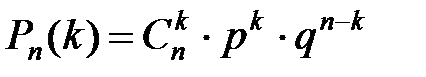 , (12)
, (12)
где k=0, 1, 2, …, n.
Данная формула и является аналитическим выражением искомого закона распределения.
Распределение, определяемое формулой Бернулли, называют биноминальным потому что правую часть равенства можно рассматривать как общий член разложения бинома Ньютона.
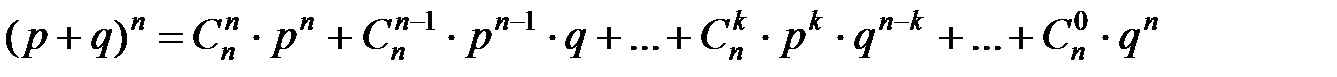 . (13)
. (13)
Таким образом, первый член разложения 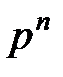 определяет вероятность наступления рассматриваемого события n раз в n независимых испытаниях; второй член
определяет вероятность наступления рассматриваемого события n раз в n независимых испытаниях; второй член 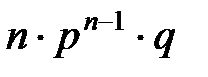 определяет вероятность наступления события
определяет вероятность наступления события 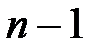 раз; …; последний член
раз; …; последний член 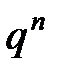 определяет вероятность того, что событие не появится ни разу.
определяет вероятность того, что событие не появится ни разу.
Напишем биноминальный закон в виде таблицы:
Таблица 2 – Биноминальный закон
| X | n | n-1 | … | k | … | 0 |
| Р | 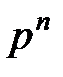
| 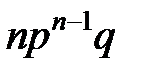
| … | 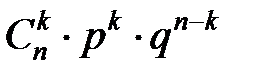
| … | 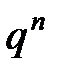
|
Математическое ожидание для биноминального распределения имеет вид:
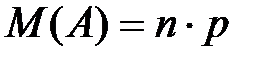 , (14)
, (14)
Пример 8:
Монета брошена 2 раза. Написать в виде таблицы закон распределения случайной величины Х – числа выпадений «герба».
Решение:
Вероятность появления герба в каждом бросании монеты 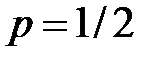 , следовательно, вероятность непоявления герба
, следовательно, вероятность непоявления герба 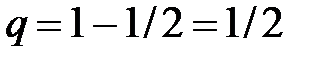 .
.
При бросании монеты «герб» может появиться либо 2 раза, либо 1 раз, либо совсем не появиться. Таким образом, возможные значения Х таковы: 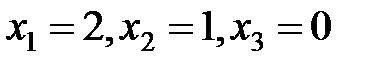 .
.
|
|
|
Найдём вероятности этих возможных значений по формуле Бернулли:
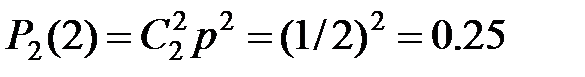
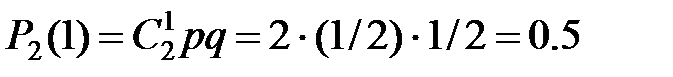
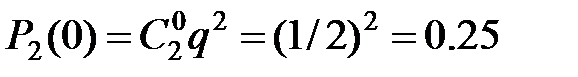
Напишем искомый закон распределения:
Х 2 1 0
Р 0.25 0.5 0.25.
Распределение Пуассона
Для того чтобы найти вероятность того, что при очень большом числе испытаний, в каждом из которых вероятность события очень мала, событие наступит ровно k раз ( при 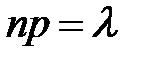 , n – число независимых испытаний, p – вероятность наступления события А) воспользуемся законом распределения Пуассона вероятностей массовых (n – велико) и редких ( p – мало) событий.
, n – число независимых испытаний, p – вероятность наступления события А) воспользуемся законом распределения Пуассона вероятностей массовых (n – велико) и редких ( p – мало) событий.
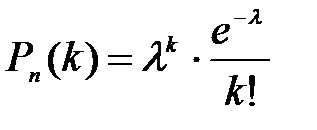 (15)
(15)
Математическое ожидание в этом случае имеет вид:
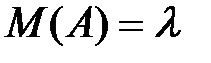
Пример 9.
Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равно 0.0002. Найти вероятность того, что на базу прибудут три негодных изделия.
Решение.
По условию, 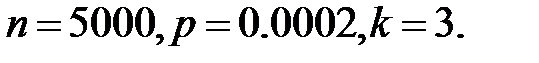 Найдём
Найдём 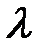
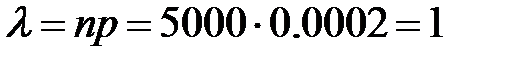 .
.
По формуле Пуассона искомая вероятность приближённо равна
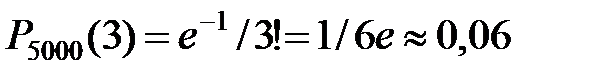
Дата добавления: 2021-04-15; просмотров: 117; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
