Процессов и структура подсистем САПР (2 ч) 10 страница

⇐ ПредыдущаяСтр 10 из 16Следующая ⇒

2. Критерий оптимальности должен выражаться количественно, то есть числом (килограммы, тонны, метры, проценты и т.д.), иначе сопоставление различных вариантов будет затруднительно.

3. Монотонность изменения критерия оптимальности при улучшении качества функционирования объекта. С этой точки зрения непригодны те параметры, которые должны иметь строго определенное оптимальное значение, отклоняться от которого нельзя 9например, если содержание какого-либо компонента в продукте строго оговорено техническим заданием, то , очевидно, оно не может выступать в качестве критерия оптимальности, а является ограничением).

Тогда в детерминированных задачах критерий оптимальности выразится функцией

. (12.1)

В статистических задачах, в которых помимо факторов α и х присутствуют ещё неизвестные факторы ξ, критерий оптимальности в общем виде может быть записан так

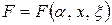. (12.2)

Так как здесь величина F зависит от неизвестных факторов ξ, то даже при заданных α и х она уже не может быть вычислена, остаётся неопределённой. В этом случае поиск экстремального значения критерия F сводится к условию: при заданных факторах α, с учётом неизвестных факторов ξ, найти такое решение 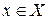, которое по возможности обеспечивает максимальное (или минимальное) значение критерия эффективности F.

Наличие неопределённых факторов переводит задачу в новое качество: она превращается в задачу о выборе решения в условиях неопределённости.

Могут быть разные подходы к решению задач в условиях неопределённости. В одних задачах имеется возможность фактор неопределённости выразить через статистические характеристики, принятые в теории вероятностей (случайные величины, случайные функции), которые для данного объекта известны или могут быть предварительно найдены. В этом случае показатель эффективности F, зависящий от случайных характеристик, также будет случайной величиной, которую, как известно, нельзя максимизировать или минимизировать и тогда в качестве показателя эффективности в принципе может быть принято её среднее значение (математическое ожидание случайной величины) . При этом задача становится детерминированной и в качестве оптимального выбирается решение х, при котором усреднённый показатель эффективности обращается в максимум или минимум:

. (12.3)

Такая оптимизация часто называется "оптимизацией в среднем".

Однако "оптимизация в среднем" не может быть использована при решении задач, в которых неизвестные факторы ξ не могут быть изучены методами теории вероятностей. Для решения таких задач иногда применяются специальные (адаптивные) алгоритмы, когда лучшее решение х достигается постепенно (путём "проб и ошибок"), т. е. направленным перебором отдельных вариантов решения задачи.

Лекция 13

Тема: Концепция оптимального проектирования. Критерии эффективности (оптимальности) в задачах векторной оптимизации (2 ч.)

План лекции: Концепция оптимального проектирования. Задачи условной и безусловной оптимизации. Общие замечания по методам оптимизации сложных систем.

13.1 Оценка альтернативных решений в многокритериальных задачах. Концепция оптимального проектирования

Процесс проектирования рассматривается как система, которая в общем виде включает в себя и то, что проектируется, и тех, кто проектирует. Обе эти составляющие проектирования соответственно определяются как проектируемая подсистема и как проектирующая подсистема. В свою очередь процесс проектирования рассматривается здесь как проявление упорядоченного воздействия проектирующей части системы на проектируемую.

Это упорядочение является следствием использования проектировщиком тех или иных методов, в основе которых лежат критерии эффективности и теория оптимизации. Их применение в проектной практике и является методологической основой оптимального проектирования. В этом смысле роль оптимального проектирования в технике та же, что и роль оптимального планирования и управления в экономике.

Используя методы оптимального проектирования, всегда можно выбрать наиболее предпочтительный вариант из многих других. Но является ли оптимальное проектирование стопроцентной гарантией успеха? К сожалению не всегда, и на то есть ряд причин. Например, такие, как возможные неточности при задании исходных данных (неточности на "входе", разумеется, приводят к неточностям на "выходе"); среди вариантов, отобранных на первой стадии решения задачи (задачи выбора), какие-то варианты, заслуживающие внимания, могут быть не учтены; наконец, многое будет зависеть от того, как, какими путями, с помощью каких средств будет реализован выбранный вариант объекта.

В инженерной практике часто приходится иметь дело с оценкой таких показателей, как стоимость, масса (вес), размеры, эксплуатационные характеристики и т.п. Опытный проектировщик эти оценки выражает обычно не в виде точных чисел, а в виде некоторых границ изменения того или иного параметра. Использование границ вместо точных чисел не является искусственным приёмом, оно является отражением реальности. Эксплуатационные характеристики машин и оборудования редко могут быть предсказаны с точностью, превышающей 10...20 % и поэтому, чтобы не вводить в заблуждение заказчика, проектировщик должен указать, является ли данное число верхней или нижней границей.

Таким образом, для некоторого множества X допустимых проектных решений должны задаваться нижние х_н и верхние х_в, границы элементов решения х при некоторых фиксированных значениях y и x, принимаемых на других уровнях проектирования объекта:

(13.1)

Представление оценок в виде границ или неравенств, а не точных чисел, оказывает неизбежное влияние на отношение конструктора к оптимизации. Трудоёмкие расчёты на ЭВМ для определения оптимума с точностью до 10-ти значащих цифр являются ярким примером бесполезных усилий, если исходные данные не могут быть заданы с точностью более трёх значащих цифр. Поэтому решения, достаточно близкие к оптимальным, могут быть получены и при значительно меньших усилиях.

Подобно большинству технических усовершенствований, оптимальное проектирование может принести большую пользу лишь при условии, что оно ведётся при полном понимании ситуации

13.2 Задачи условной и безусловной оптимизации

Задачи оптимизации с математической точки зрения обладают свойством замкнутости, т. е. свойством, позволяющим чисто математически без всякого участия проектировщика найти решение 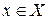, доставляющее максимум или минимум целевой функции 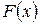на множестве X возможных решений. Получаемый при этом результат однозначно определяет экстремум функции, что свидетельствует о замкнутости задачи оптимизации (рисунок 13.1,а).

Принципиальное отличие задачи принятия решения в условиях неопределённости от задач оптимизации (или детерминированных задач принятия решения) состоит как раз в том, что они не позволяют получить однозначный результат без участия проектировщика, за которым остаётся выбор окончательного решения среди возможных альтернатив.

а) в условиях определенности; б) в условиях неопределенности

Рисуно13.1 - К определению экстремума

На рисунке 13.1, б показан именно такой случай: здесь функция эффективности 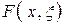скалярна, но имеет множество неопределённостей, обусловленных тремя значениями случайного фактора ξ, равных ξ₁,ξ₂ и ξ₃. В этой ситуации для каждого из этих значений случайного фактора можно найти оптимальное решение , , , но какое из них принимать за окончательное решает проектировщик (или лицо, принимающее решение - ЛПР). Такие задачи являются формально незамкнутыми.

В задачах оптимального проектирования технических объектов вектор переменных проектирования 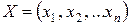выбирают в результате определения экстремума целевой функции F(Х) в области допустимых решений, которая задаётся системой ограничений на параметры проектируемого объекта.

Оптимизационные задачи, в которых экстремум целевой функции ищут в пределах неограниченного пространства переменных проектирования, называются задачами безусловной оптимизации, а найденный при этом экстремум - безусловным экстремумом.

Наличие ограничений любого вида приводит к оптимизационным задачам условной оптимизации, решение которых даёт условный экстремум.

Образно говоря, безусловный максимум, это как бы вершина горы, а условный максимум, это самая высокая точка заданной, т.е. описываемой «уравнениями связи», ограничивающими область поиска, горной тропы. То же можно сказать и о безусловном и условном минимуме: безусловный минимум, это самая низкая точка горы, а условный минимум - самая низкая точка горной тропы.

В задачах безусловной оптимизации независимые переменные х₁, х₂…. не связаны между собой никакими соотношениями, тогда как в задачах условной оптимизации независимые переменные связаны между собой определенными соотношениями, представляющими собой так называемые уравнения связи или условия ограничения.

Экстремумы целевой функции могут быть также локальными и глобальными:

а) локальные экстремумы определяются в малой окрестности точки экстремума, тогда как глобальный экстремум определяется во всей области допустимых значений;

б) функция F(Х) имеет в данной точке 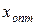локальный экстремум, если существует такая малая двусторонняя окрестность этой точки, что для всех остальных точек х этой окрестности выполняется одно из двух условий:

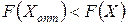(13.2)

и тогда точка 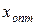. является локальным минимумом функции F(Х),

или

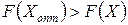(13.3)

и тогда точка 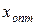является локальным максимумом функции F(Х);

в) функция F(Х) имеет в данной точке 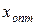глобальный экстремум, если для всех остальных точек X, находящихся в пределах области допустимых значений, выполняется одно из двух условий:

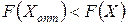(13.4)

и тогда точка 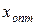является глобальным минимумом функции F(Х),

или

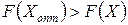(13.5)

и тогда точка 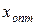является глобальным максимумом функции F(Х).

Задачиэтого класса могут решаться с использованием классических методов вариационного исчисления, которое, в основном, примыкает к теории максимумов и минимумов. Использование этих методов связано с определёнными условиями, которым должна удовлетворять исследуемая функция F(Х) для этой функции должно быть известно аналитическое выражение, она должна быть по крайней мере дважды дифференцируема по всем переменным .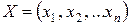

Из теории максимумов и минимумов известно, что всякая дифференцируемая функция может достигать экстремума только в тех точках, в которых её частные производные обращаются в нуль. Такие точки называются стационарными.

Условия

(13.6)

являются необходимыми условиями экстремума.

Однако не все стационарные точки обязательно являются точками экстремума. Поэтому каждая из стационарных точек должна быть проверена на экстремум с помощью достаточныхусловий экстремума.

В САПР поиск глобального критерия осуществляется путём локальной оптимизации из нескольких исходных точек, выбираемых случайным образом в пределах области допустимых решений. При этом находят несколько локальных экстремумов, из которых выбирают наилучший.

При решении задач безусловной оптимизации широко применяются методы поиска оптимальных точек, основанные на сплошном или направленном переборе возможных вариантов проектных решений (методы "сплошного" и "направленного" перебора). При применении последнего метода допустимая область переменных параметров делится определенным образом, что позволяет значительно сократить объём расчётов по сравнению с методом сплошного перебора.

Наиболее важными элементами поисковых методов оптимизации являются: выбор направления движения к оптимуму, выбор оптимальной длины шага поиска и момент окончания поиска.

Алгоритмы поисковых методов оптимизации реализуются программными средствами на ЭВМ.

13.3 Общие замечания по методам оптимизации сложных систем

Основным методом поиска эффективности вариантов сложных систем является математическое моделирование. Моделирование системы основано при этом на составлении модели процесса функционирования системы, с помощью которой входные и варьируемые параметры системы связываются с показателями её эффективности.

Основными методами моделирования, с помощью которых производится описание процесса функционирования системы и оценка ее эффективности, являются аналитический и алгоритмический методы.

Аналитические модели записываются обычно в виде результатов аналитического решения соотношений некоторой исходной модели. При этом модели, описывающие детерминированные системы, в аналитической форме представляют собой явные выражения выходных параметров (или выходных переменных системы) как функции входных параметров (или входных переменных). При использовании аналитических моделей при исследовании процессов с учётом случайных факторов возникают определённые трудности, связанные как с получением уравнений, содержащих в качестве переменных законы распределения или другие вероятностные характеристики (средние значения или математические ожидания, дисперсии, корреляционные функции, спектральные плотности и т. д.) исследуемых процессов, так и решением полученных уравнений.

Алгоритмические модели представляют собой запись определенных соотношений модели в форме алгоритма. Здесь не требуется преобразовывать аналитические выражения в специальную систему уравнений относительно искомых величин. Для них характерно воспроизведение на ЭВМ описываемых явлений, лишь с сохранением логической структуры явлений и порядка их наступления, что обеспечивается заданным моделирующим алгоритмом.

Примерами аналитических моделей, используемых для оценки различных вариантов системы и нахождения её оптимального варианта являются задачи математического программирования в их традиционной постановке, предполагающую аналитическую запись соответствующих функционалов (целевых функций) и ограничений. Если же при оптимизации системы традиционная постановка задачи математического программирования оказывается невозможной, то в этом случае приходится прибегать к другим математическим методам или использовать эвристические методы поиска оптимальных вариантов, например, метод экспертных оценок.

К более точным оценкам приводит использование имитационных моделей (или статистических моделей, реализуемых на ЭВМ).

Примерами имитационных моделей являются модели массового об служивания, предназначенные для имитации различных процессов обслуживания (например, обслуживание погрузки и разгрузки различных транспортных средств, и т. п.).

Имитационные модели, предназначенные для имитации физических или информационных процессов, обычно представляются в алгоритмической форме.

Для математического описания систем массового обслуживания в принципе можно было бы при некоторых предположениях относительно структуры системы использовать аналитические методы решения задачи, но полученные оценки не отличались бы при этом высокой точностью, т. к. для реальных систем массового обслуживания характерно большое количество случайных факторов (например, время и интервалы поступления заявок на обслуживание, количество линий обслуживания и время их занятости и т. д.). Если не пренебрегать всеми этими факторами, то об аналитическом решении задач массового обслуживания не может быть и речи. Вместе с тем метод статистического моделирования (или метод Монте-Карло) позволяет получать решение подобных задач без упомянутых ограничений, учитывая действие реально действующих случайных факторов.

Не рассматривая здесь подробно процедуры, связанные с использованием метода статистического моделирования, укажем лишь, что идея этого метода состоит в том, что вместо описания исследуемого процесса с помощью аналитического аппарата (дифференциальных или алгебраических уравнений), на ЭВМ воспроизводится многократная реализация случайного процесса, после чего результаты всех реализаций обрабатываются методами математической статистики и находятся средние значения (математические ожидания), вероятности событий, дисперсии случайных величин и другие интересующие нас характеристики случайного процесса.

Из-за сложности исследуемых систем при их оптимизации в рамках задач математического программирования или с помощью метода статистического моделирования часто прибегают к построению многоэтапных или итеративных процедур оптимизации систем.

Так, например, при двухэтапной процедуре оптимизации, на первом этапе производится оптимизация системы в рамках традиционной задачи математического программирования. При этом оценка эффективности вариантов системы производится любым из доступных и наиболее точных методов (аналитическое моделирование, экспертные оценки). На втором этапе некоторое число вариантов системы, отобранных на первом этапе по наибольшим (или наименьшим) значениям целевой функции по сравнению с другими рассмотренными вариантами, подвергаются исследованию методом статистического моделирования, по результатам которого производится окончательный отбор оптимального варианта системы.

Дата добавления: 2021-04-15; просмотров: 46; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 5 6 7 8 91011 12 13 14 Следующая ⇒

Мы поможем в написании ваших работ!