Процессов и структура подсистем САПР (2 ч) 8 страница

Рисунок 10.1 – Блочная структура проектируемого объекта

Моделями элементов блока А являются уравнения, связывающие входные и выходные переменные:

(10.1)

В векторной форме полная модель блока А, состоящего из пяти элементов и соответственно из пяти моделей каждого элемента, запишется так:

(10.2)

где V, U и Z - векторы внутренних, входных и выходных фазовых переменных.

Полная модель составлена здесь из микромоделей элементов данного блока.

При переходе к более высокому иерархическому уровню, т. е. от микромоделей к макромодели, из модели (10.2) блока следует исключить вектор внутренних переменных V, т. к. макромодель будет описывать только взаимодействие между блоками объекта, а не внутренние связи между элементами каждого блока. Полученная таким образом макромодель представляет собой систему уравнений

(10.3)

размерность которой существенно меньше, чем модели (10.2).

10.2 Структура математических моделей объектов, проектируемых в САПР

При проектировании сложных технических объектов в САПР используются два основных вида моделей, отличающихся своей структурой и представляющих собой преобразованную исходную математическую модель объекта: многоуровневые (тандемные) модели и сетевые модели.

Многоуровневые модели. Модели этого вида отражают такую схему процесса проектирования объекта, при которой от одного уровня к другому происходит детализация объекта. На первом уровне учитываются лишь основные факторы, влияние которых на изучаемые свойства объекта наиболее значимо. На втором и последующих уровнях с учетом результатов, получаемых на предыдущих уровнях проектирования, происходит более полное математическое описание и детализация объекта. При этом на каждом уровне проектирования (т. е. на каждом этапе решения проектной задачи) переменные математической модели ранжируются по степени важности их влияния на характеристики объекта.

Подобное представление совокупности моделей в канонической форме (в виде некоторой линейной суммы моделей) характерно для многоуровневых моделей, получивших название тандемных моделей. Такие модели отражают вертикальные информационные связи между соответствующими проектными модулями.

Важным свойством тандемных моделей является возможность переменные, присутствующие в моделях каждого уровня, определить через переменные моделей более низких уровней.

В общем случае на базе исходной модели может быть сформировано множество тандемных моделей, отличающихся одинаковыми признаками.

Тандемные модели обычно целиком не формируются заранее, они получаются путём агрегирования из различного числа элементарных моделей, составляющих соответствующие модули ППП. Если моделью первого уровня является элементарная модель, то модели второго и последующего уровней могут быть уже агрегированными, имея в своём составе несколько элементарных моделей.

Сетевая структура моделей подразумевает агрегирование исходной математической модели в подмодели и элементарные модели, описывающие составные части (подсистемы) и элементы объекта; по сравнению с исходной моделью такие модели дают более приближённое описание объекта.

Структура такой модели изображается в виде графа, в котором вершины х _i, соответствуют операторам элементарных моделей, а дуги, соединяющие вершины, определяют информационные связи между ними, причём входящие дуги каждой вершины представляют собой векторы входов а исходящие - векторы выходов (рисунок 10.2).

Такое представление структуры моделей часто применяется при решении задач планирования вычислений на пакете прикладных программ модульной структуры, когда требуется гибкое построение различных расчётных схем при формировании соответствующих программных модулей.

Рисунок 10.2 - Сетевая структура математической модели,

представленной в виде графа

Гибкость исходной модели зависит от числа агрегированных моделей - чем больше степень разбиения исходной модели на элементарные модели, тем больше гибкость исходной модели и тем больше возможность на одной и той же модели решать задачи в различных постановках. При этом переменные, которые в одних задачах являются входными, в других могут быть выходными и наоборот. Следует, однако, заметить, что такого рода гибкость допустима лишь при описании структуры модели в виде неориентированного графа, в котором нет деления дуг (векторов), связывающие элементарные модели (вершины графа) на входные и выходные.

Разделение исходной модели на элементарные модели производится при ее программной реализации, что исключает влияние способов реализации на процедуры формирования проектных модулей САПР.

Если структура исходной модели представляется в виде ориентированного графа, то в этом случае допускается формирование лишь такзо агрегированных моделей, у которых входы и выходы строго обусловлен, входами и выходами, содержащимися в исходной модели. Таким образом, способ формирования агрегированных моделей - на базе неориентированных или ориентированных графов - также влияет на гибкость исходной модели.

Если многоуровневые тандемные модели являются базой для формирования вертикальных связей между проектными модулями, то сетевая структура моделей характерна для отображения горизонтальных связей между проектными модулями.

Горизонтальные проектные связи между каждой парой проектных модулей имеют место, если результаты выполнения проектных процедур на каждом из них являются взаимозависимыми в том смысле, что имеется возможность выражения одних переменных модели через другие с помощью связей, заложенных в исходной модели проектируемого объекта. Или, другими словами, когда проектные решения двух взаимозависимых проектных модулей могут быть выражены друг через друга с помощью связей соответствующей математической модели.

10.3 Имитационное моделирование в САПР. Вычислительный эксперимент

Сложность и многообразие проектируемых объектов не всегда позволяет всю необходимую информацию о влиянии многочисленных факторов на его функционирование получить при проведении физического эксперимента. В других случаях проведение физических экспериментов может быть сопряжено с большими материальными затратами, а порой и с большой опасностью.

В подобных ситуациях исследователь обращается к имитационному моделированию объектов на ЭВМ.

Имитационная система состоит из двух частей, одна из которых с помощью программных средств обеспечивает формирование математической модели, воспроизводящей условия опыта, а другая - дает возможность целенаправленно управлять экспериментом в соответствии с заданным алгоритмом.

Имитационное моделирование, по сути, представляет собой вычислительный эксперимент, проводимый на базе некоторой математической модели по разработанному алгоритму. Такой алгоритм определяет последовательность арифметических и логических операций, которая реализуется в виде программы-имитатора на ЭВМ. При этом в ЭВМ имитируется функционирование исследуемого объекта с учётом выбранного уровня детализации при варьируемых в заданных границах значениях параметров объекта и изменяющихся начальных условиях. Имитационные программы имеют модульную структуру, в которой модули связаны между собой по типовой или заданной схеме.

Известны два подхода к организации имитационных моделей. Один из них заключается в том, что каждый элемент сложного объекта описывается элементарной моделью - программным модулем; сопряжение между модулями формируется по специальной схеме, отражающей структурную и функциональную специфику объекта.

Другой подход предусматривает конструирование универсальной имитационной модели, на базе которой может быть исследован любой объект данного класса. В этом случае структурные и функциональные характеристики объекта, отличающие его от других объектов того же класса, не должны входить в структуру и описание модели, а должны быть легко заменяемыми исходными данными.

Возможности вычислительного эксперимента велики по сравнению с натурными экспериментами. Вычислительный эксперимент быстрее, дешевле, проще и легко управляем. В него можно вмешиваться в ходе проведения эксперимента, точно сохранять значения переменных при повторном проведении каждого опыта и моделировать условия, которые невозможно создать в лаборатории.

Следует также отметить, что численные методы решения задач, используемые при проведении вычислительного эксперимента, позволяют легко перестраиваться с решения одних задач на другие, тогда как экспериментальное оборудование, приспособленное для изучения одних физических процессов, не может быть столь же легко перестроено для изучения других физических процессов.

Но есть у вычислительного эксперимента один существенный недостаток: применимость его результатов ограничена рамками принятой математической модели, которая в свою очередь строится на основе изучения физических закономерностей, выявляемых при проведении физического эксперимента.

Лекция 11

Тема: Разработка комплексной модели качества (2 ч.)

План лекции: Понятие «качество». Основные требования математической модели - адекватность, чувствительность, устойчивость

11.1 Понятие «качество»

Термин «качество» существует около 2500 лет – со времен Аристотеля и имеет несколько трактовок:

- качество – это существенная определенность объекта, в силу которой он является данным, а не другим объектом, т.е. это та самая определенность, которая отличает лошадь от стола. Эта трактовка была основной вплоть до 20 века.

- качество – это один из существенных признаков, свойств, особенностей, характеризующих данный объект, например, теплота, холодность и т.д.

- качество – это совокупность свойств объекта, проявляющихся в процессе его использования по назначению.

Согласно современной трактовке качество продукции – это совокупность свойств продукции, обусловливающих её пригодность удовлетворять определенные потребности в соответствии с её назначением.

В настоящее время используют еще два термина:

- главное качество – качество, отождествляемое с каким-то одним определяющим, доминирующим свойством, характеризующим потребительскую стоимость данного продукта труда;

- интегральное качество – качество, определяемое совокупностью всех функциональных, эстетических, и экономических свойств, т.е. выражаемое совокупностью потребительской стоимости и суммарных затрат на производство и потребление этого продукта труда.

11.2 Комплексная модель качества

Для разработки комплексной модели качества составляется математическая модель технического объекта (продукции), т.е. совокупность математических объектов (чисел, переменных, матриц, множеств и т.д.) и отношений между ними, которая адекватно отражает свойства технического объекта. Выполнение проектных операций и процедур в САПР основано на оперировании математическими моделями. С их помощью прогнозируются характеристики и оцениваются возможности предложенных вариантов схем и конструкций, проверяется их соответствие предъявляемым требованиям, проводится оптимизация параметров, разрабатывается техническая документация и т.д.

Основными требованиями, предъявляемыми к математическим моделям, являются требования адекватности, чувствительности и устойчивости.

Адекватность. Модель считается адекватной, если отражает заданные свойства объекта с приемлемой точностью. Точность определяется как степень совпадения значений выходных параметров модели и объекта. Если х_М_i значение выходного i-го параметра, x_oi – значение того же i-го параметра объекта, то относительная погрешность:

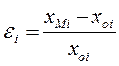, (11.1)

Погрешность модели по совокупности учитываемых m параметров:

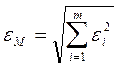, i=1,2,…,m (11.2)

При заданной допустимой погрешности должно выполняться условие .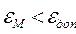

Чувствительность модели характеризует, как изменяется выходные параметры модели при различных вариациях выходных параметров.

Устойчивость модели определяет, насколько изменяется выходная величина при изменении выходной величины, вызванным погрешностью измерений или упрощением соотношений, входящих в математическую модель.

Правильно построенная и удовлетворяющая указанным требованиям математическая модель позволяет не только описать поведение и свойства объекта в данной конкретной ситуации, но и предсказать, как объект будет себя вести в данных условиях при изменении его параметров.

Таким образом, математическая модель реальной системы (процесса) это совокупность соотношений (имеющих форму уравнений, неравенств, логических условий и т.д.), которые связывают характеристики процесса с параметрами соответствующей системы, исходными данными и начальными условиями.

Математическим описанием объекта можно считать систему уравнений:

У_i=F_i (Х,Н). (11.3)

Конкретный вид функции системы можно получить, исходя из двух принципиально разных подходов: структурного и эмпирического.

Для целей моделирования используют пассивные и активные эксперименты. В пассивных экспериментах нет возможности выбирать условия опыта по своему усмотрению и устанавливать значения факторов на желаемом уровне. В активных экспериментах опыты проводятся по заранее разработанному плану, выражающему количество опытов и значения факторов в каждом опыте.

План, содержащий запись всех комбинаций факторов или их части в кодированном форме, называют матрицей планирования. Таблицы планов можно найти в специальной литературе

Для нахождения вида уравнений системы (11.3) обычно пользуются тем, что большинство функций, встречающиеся на практике можно разложить в степенной ряд Тейлора. Если ограничится несколькими первыми членами ряда, то функция отклика будет представлена многочленом (полиномом) вида:

У=b_о+b₁х₁+b₂х₂+b_nх_n+b₁₁х₁²+b₂₂х₂²+b_nnх_n²+b₁₂х₁х₂+b₁₃х₁х₃+…

+b₁_nх₁х_n+b₁₁₁х₁³+b_nnnx_n³+…, (11.4)

где b_i, b_ij и т.д. – эмпирические коэффициенты.

Выбор вида эмпирических формул можно произвести по типичным графикам некоторых формул, приведенных в специальной литературе и некоторых справочниках по математике. Числовые коэффициенты, входящие в формулы, либо определяются непосредственно из графических зависимостей , либо специальными методами – например, методом наименьших квадратов или способом средних .

На использовании метода наименьших квадратов базируется и теория планирования эксперимента, использование которой позволяет при сравнительно небольшом количестве экспериментальных данных рассчитать значения числовых коэффициентов в многочлене вида (11.4) , иначе называемом уравнением регрессии. Описание методов планирования эксперимента и рекомендации по их применению можно найти в специальной литературе.

Расчет коэффициентов уравнения регрессии проводят формуле:

(i=1,2,….N), (11.5)

где Y_u - среднее значение по параллельным опытам u-той строки

матрицы планирования.

(k=1,2,…N), (11.6)

где m – число параллельных опытов;

Y_uk - значение Y_u для каждого опыта u-той строки.

Объединив формулы (3) и (4) , можно вычислить коэффициенты регрессии:

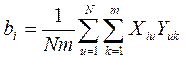(11.7)

Так как один фактор влияет на переменную состояния больше, а другой меньше, то необходимо проводить оценку значимости коэффициентов регрессии двумя способами. В обоих случаях сначала находят дисперсию коэффициентов регрессии по формуле:

, (11.8)

Т.е. дисперсии всех коэффициентов равны, поскольку зависят от ошибки опыта S₀² и числа строк матрицы планирования N.

, (11.9)

Где N (m-1)=f₀ – число степеней свободы.

По первому способу оценивают значимости коэффициентов осуществляют по формуле:

и условию t_ip>t_t, (11.10)

Где - абсолютное значение i–го коэффициента регрессии;

t_t - табличное значение критерия Стьюдента, которое находится по числу степеней свободы и уровню значимости q(q=0,05);

S_bi - среднеквадратичное отклонение b_i.

Дата добавления: 2021-04-15; просмотров: 42; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 3 4 5 6 789 10 11 12 Следующая ⇒

Мы поможем в написании ваших работ!