Процессов и структура подсистем САПР (2 ч) 7 страница

⇐ ПредыдущаяСтр 7 из 16Следующая ⇒

В этом случае исследуемую систему S мысленно расчленяют на ряд подсистем таким образом, чтобы построение математической модели каждой из подсистем было заведомо возможно. Пусть характеристиками подсистем будут функции , а в качестве параметров – величины .

При сделанных предположениях математические модели для подсистем S_i могут быть выражены соотношениями

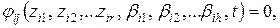(8.13)

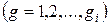
Так, для подсистемы математическая модель представится системой уравнений:

(8.14)

подсистемы :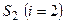

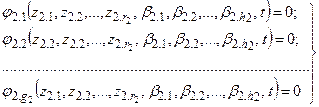(8.15)

для подсистемы :

(8.16)

Но совокупность моделей вида (8.13) для подсистем S_i, рассматриваемых совместно для всех i = 1,2,...т, в общем случае ещё не составляет математическую модель для всей системы. Эта совокупность пока характеризует лишь отдельные изолированные подсистемы S_t

Поэтому, помимо соотношений (6.13) необходимо иметь соотношения вида

(8.17)

связывающего характеристики подсистем S_i с характеристиками х₁, x₂,… x_n системы S.

Для получения общего вида уравнений модели для сложных систем обычно прибегают к предварительному построению так называемых экви валентных схем, с помощью которых легче установить физический смысл математической модели и её структуру.

Лекция 9

Тема: Классы математических моделей. Способы реализации математических моделей на ЭВМ (2 ч.)

План лекции: Классы математических моделей. Формализованные (эквивалентные) схемы объектов проектирования. Способы реализации математических моделей на ЭВМ. Формализация проектных процедур и объектов проектирования в САПР.

9.1 Классы математических моделей

Классификационные признаки математических моделей обычно связываются с используемым математическим аппаратом и математической символикой, с формой представления моделей, с классами систем, описываемыми моделями, с характером решаемых задач.

Математические модели могут быть классифицированы по следующим признакам.

1 По используемому математическому аппарату и форме представления:

дифференциальные и алгебраические уравнения, неравенства. Для линейных систем, описываемых однородными уравнениями, алгебраическими или дифференциальными с постоянными коэффициентами и содержащими несколько переменных, математическая модель может быть представлена в матричной форме. Модели могут быть также представлены в виде логических условий (схемы алгоритмов, программы расчётов на ЭВМ), графических образов (графики, диаграммы, эквивалентные и структурные схемы, графы).

2 По виду записи, отражающей способ действия над моделью:

инвариантная, т. е. запись в виде выражений с помощью традиционного математического языка безотносительно к методу решения уравнении модели;

аналитическая - запись модели в виде результата аналитического решения исходных уравнений модели, выраженного соответствующей формулой;

алгоритмическая - запись соотношений модели и выбранного численного метода в форме алгоритма.

3 В зависимости от свойств системы, которые отражают мо дели:

функциональные модели, описывающие процессы функционирования системы;

структурные модели, описывающие структурные свойства системы, например, её геометрию, размеры, взаимное расположение частей и элементов системы в пространстве. Такие модели связаны с конструкторскими аспектами проектирования систем.

4 По своему назначению:

имитационные модели, предназначенные для имитации физических и информационных процессов, происходящих в системе. На базе таких моделей оказывается возможным проводить так называемый вычислительный эксперимент, в основе которого лежит некоторый вариант математической модели, с помощью которой, варьируя различными параметрами задачи (значениями коэффициентов уравнений, начальными или граничными условиями и др.) можно провести детальное исследование изучаемого процесса в рамках модели, не прибегая к натурному эксперименту или к использованию физических моделей;

оптимизационные модели, предназначенные для выявления такого состояния системы или для нахождения таких её параметров, которые по принятому критерию будут наилучшим образом удовлетворять поставленным требованиям, Иными словами, оптимизационные модели имеют целью ответить на вопрос - "как должно быть?";

дескриптивные модели, предназначенные для объяснения наблюдаемых явлений или для прогноза поведения системы. Такие модели отвечают на вопросы - "как это происходит?", "как это будет развиваться?".

5 В зависимости от класса систем, описываемых моделями, различают детерминированные и статистические модели. В моделях первого типа между функцией и аргументом существует функциональная зависимость, а в моделях второго типа - статистическая зависимость.

6 В зависимости от уровня абстрагирования (или огрубления) исследуемых объектов различают микро-, макро- и мегамодели.

Наименьшую степень абстракции имеют микромодели, которые наиболее полно описывают процессы, происходящие внутри отдельных частей системы (подсистем, блоков). Такие модели позволяют объяснить состояние системы, например, напряжённое состояние или причину де формации конструкции, тепловое состояние её элементов и т. д.

Большую степень абстракции имеют макромодели, которые уже не учитывают изменение состояния внутри подсистем и их элементов, а отражают лишь внешние их свойства, не объясняя чем и как они вызваны.

Наибольшая степень абстракции допускается при построении мега-моделей. Если в макромоделях описываются процессы, происходящие между подсистемами (но не внутри их), то в мегамоделях описываются лишь процессы между системой и внешней средой или между отдельными системами.

Математические модели, отображающие поведение объекта и описывающие лишь воздействия на его входах и реакции объекта на входные сигналы, часто называется "черным ящиком".

7 В зависимости от класса математических задач в прикладных разделах математики.

Здесь характерным примером являются математические модели "исследования операций" и, в частности, модели математического программирования, модели случайных процессов (монте-карловские модели), модели массового обслуживания, модели теории игр.

9.2 Формализованные (эквивалентные) схемы объектов проектирования

При математическом описании динамических систем, отличающихся структурной и функциональной сложностью, обычно используется две формы их математического описания: схемная в виде эквивалентных схем объекта проектирования и формирование математической модели объекта с помощью дифференциальных уравнений движения. Эти формы математического описания объектов в задачах динамики часто применяются совместно: вначале строится эквивалентная схема, с помощью которой исследователю легче представить структуру исследуемого объекта, связи между его элементами, а затем по результатам анализа эквивалентной схемы объекта описать процесс его функционирования с помощью дифференциальных уравнений движения.

Построению эквивалентной схемы объекта предшествует содержательное описание и общая постановка прикладной задачи с указанием известных количественных характеристик и параметров объекта, особенности его функционирования и взаимодействия с другими объектами или с внешней средой.

При построении эквивалентной схемы объекта должны быть соблюдены определенные условия, а именно: сохранение баланса кинетической и потенциальной энергий, которым обладала реальная исходная динамическая система, а также сохранение неизменного значения мгновенных мощностей, развиваемых внешними силами. Выполнение этих условий связано с необходимостью замены реальных значений основных динамических параметров системы (масс, моментов инерции, жесткостей упругих элементов и сил) их приведёнными значениями.

Приведённые значения масс и моментов инерции определяются из условия равенства кинетической энергии приведённой массы (приведённого момента инерции) кинетической энергии массы или момента инерции системы, которые они заменяют.

В составе математического описания, можно выделить следуйте группы уравнений:

- уравнения баланса масс и энергии, записанные с учетом гидродинамической структуры потоков, составленные раздельно по веществам и составным частям объекта, либо по всему объекту в целом;

- уравнения "элементарных" процессов для отдельных элементов объекта - описания процессов тепло- и массообмена, реакций и т. д.;

- теоретические, полуэмпиричаские или эмпирические соотношения между различными параметрами 'процесса, например, зависимости коэффициента массоотдачи от скоростей потоков фаз, зависимость теплоемкости раствора от концентрации компонентов и т. д.;

- ограничения, накладываемые на параметры объекта и процесса.

Общим для всех математических моделей является то, что число уравнений и различных соотношений, включаемых в математическое описание, должно быть равно числу определяемых параметров (иначе система будет иметь бесконечное число решений).

Значительное влияние на выбор метода решения системы уравнений математического описания и решение задач оптимизации оказывает конкретный вид уравнений математического описания. Для характеристики свойств различных объектов в химической технологии обычно используются конечные алгебраические (трансцендентные) уравнения, обыкновенные дифференциальные уравнения и уравнения в частных производных, а также (очень редко) интегральные управления.

К конечным алгебраическим уравнениям обычно сводится математическое описание стационарных режимов работы объектов с сосредоточенными параметрами. Кроме того, уравнения этого типа применяют также при математическом описании более сложных объектов для выражения стационарных связей между разными параметрами.

Обыкновенные дифференциальные уравнения обычно используются для математического описания нестационарных (динамических, изменяющихся со временем) объектов с сосредоточенными параметрами. А также стационарных режимов объектов с распределенными параметрами, в которых значения параметров зависят только от одной пространственной координаты.

Дифференциальные уравнения в частных производных используются для математического описания динамики объектов с распределенными параметрами или стационарных режимов объектов, в которых параметры зависят от двух и более пространственных координат.

Любой технологический процесс, как правило, сопровождается перемещением жидкости, газа или твердых частиц. В связи с этим особое значение в задачах математического моделирования приобретает описание движения потоков как основы для составления математической модели объекта.

9.3 Способы реализации математических моделей на ЭВМ

Математические модели современных технических систем реализуются, как правило, с помощью ЭВМ. Но в зависимости от характера, сложности и структуры математических моделей способы их реализации на ЭВМ и сама роль вычислительной техники, в этом процессе могут быть различными.

С этой точки зрения можно выделить математические модели, решаемые аналитическими, численными и алгоритмическими методами. Последние в специальной литературе нередко определяются как методы моделирования процессов на ЭВМ. Однако такое определение весьма условно, т.к. под моделированием обычно понимается любой способ исследования систем и процессов на моделях независимо от методов их решения и формы представления промежуточных или конечных результатов, полученных при реализации модели.

Для исследователя наиболее привлекательны аналитические методы исследования, позволяющие получить результат в виде явных формул для искомых величин, либо в виде уравнений, для которых решения известны. Подобная форма представления результатов наиболее удобна для анализа процессов функционирования исследуемых или проектируемых объектов и для поиска их оптимальных вариантов.

Но в случаях, когда не удаётся преобразовать математическую модель в подходящую систему уравнений, а её упрощение приводит к недопустимому огрублению результатов, от аналитического исследования приходится отказаться и перейти к другим методам исследования, например, к исследованию численными методами.

Как и при использовании аналитических методов, численные методы решения обязательно связаны с необходимостью преобразования ис ходной модели в специальную систему уравнений относительно иско мой величины. Разница заключается лишь в том, что при использовании аналитических методов исходная модель преобразуется в уравнения, допускающие аналитическое решение, а во втором случае - допускающие эффективное использование одного из численных методов, причём в обоих случаях решения могут быть выполнены либо вручную, либо на ЭВМ. При реализации этих методов с применением вычислительной техники, её роль сводится к автоматизации вычислений.

Существенное отличие третьего - алгоритмического - метода исследования систем и процессов от первых двух состоит в том, что в этом случае не обязательно преобразовывать исходную математическую модель в специальную систему уравнений относительно искомых величин, необходимо лишь с помощью соответствующего моделирующего алгоритмапрограммы, реализующей этот алгоритм, задать ЭВМ такую последовательность выполнения операций, при которой была бы сохранена логическая структура явлений, описываемых математической моделью, и последовательность их чередования во времени. Вэтом случае роль ЭВМ заключается не столько в выполнении чисто вычислительных операций, сколько в воспроизведении явлений, описываемых математической моделью. Если при использовании обычных численных методов исследования первоначальная математическая модель преобразовывается в систему уравнений относительно искомых величин, которые по своей логической структуре далеки от самой математической модели до ее преобразования, так и от процесса, описываемого этой моделью, и ЭВМ выполняет операции, непосредственно связанные с особенностями данного численного метода, а не с моделью процесса, то при алгоритмическом методе исследования реализация моделирующего алгоритма является в некотором смысле имитацией элементарных явлений, составляющих исследуемый процесс.

В отличие от аналитического и численного метода исследования, содержание операций, выполняемых ЭВМ при алгоритмическом моделировании, не находится в прямой зависимости от величин, выбранных в качестве искомых. Здесь, как и при физическом моделировании или при проведении натурных экспериментов для оценки искомых величин может быть использована любая информация, которую несёт в себе математическая модель, но которая доступна регистрации и последующей обработке. Поэтому при таком способе моделирования пользователь при желании может получить информацию не только по искомой величине, но и другим характеристикам исследуемой системы. Например, при исследовании какого-либо случайного процесса в результате моделирования могут быть зафиксированы (выданы "на печать") не только средние значения (математическое ожидание тех или иных параметров объекта), но и другие вероятностные характеристики: дисперсии, корреляционные моменты, законы распределения и т.д.

Таким образом, при использовании алгоритмического метода моделирующий алгоритм можно рассматривать как одну из форм записи математической модели.

Моделирующий алгоритм обычно составляется не в виде машинной программы которая учитывает особенности системы команд той или иной ЭВМ а в виде операторной схемы, содержащей последовательность операторов каждый из которых изображает выполнение определённых элементарных операций. Такое представление моделирующего алгоритма оставляет некоторую свободу выбора типа ЭВМ.

Лекция 10

Тема: Иерархия математических моделей в САПР .Имитационное моделирование в САПР (2 ч.)

План лекции: Иерархия математических моделей в САПР. Структура математических моделей объектов, проектируемых в САПР. Имитационное моделирование в САПР. Вычислительный эксперимент.

10.1 Иерархия математических моделей в САПР

Блочно-иерархический подход к проектированию включает в качестве своей основы иерархию математических моделей. Деление модели по иерархическим уровням (уровням абстрагирования) происходит по степени детализации описываемых свойств объекта и процессов, протекающих в объекте. При этом накаждом иерархическом уровне используют свои понятия "система" и "элемент". Так, например, при моделировании какой-либо машины её трансмиссия может рассматриваться как одна из её подсистем, а составляющие части трансмиссии (коробка передач, главная передача, карданные передачи) - как элементы данной системы. Но та же трансмиссия при рассмотрении её отдельно, не в системе машины, может быть принята за систему, а составляющие её части за подсистемы; тогда детали каждой из этих частей, например, шестерни и валы КП принимаются за элементы системы.

В соответствии с уровнями абстрагирования строятся микро-, макро- и мегамодели.

Наиболее полной является микромодель, составленная из моделей элементов системы с учётом межэлементных связей, т. е. модель, описывающая состояние каждого элемента и его выхода.

Представим, например, структуру некоторого объекта в виде множества элементов и связей между ними и в соответствие с блочно-иерархическим подходом в структуре объекта выделим подмножество элементов, составляющих блоки (подсистемы) объекта; на рисунке 6.1 эти блоки показаны штриховыми линиями. Пусть состояние каждого элемента характеризуется внутренними переменными V_i;, описывающими внутренние связи между элементами данного блока, а также переменными u_i, и z_i на входах и выходах блока.

Дата добавления: 2021-04-15; просмотров: 45; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 2 3 4 5 678 9 10 11 Следующая ⇒

Мы поможем в написании ваших работ!