Процессов и структура подсистем САПР (2 ч) 6 страница
Типовыми задачами одновариантного анализа являются;
1. Анализ статического состояния.
2. Анализ переходного процесса.
3. Анализ частотных характеристик.
4. Анализ устойчивости.
5. Анализ стационарных режимов колебаний.
Для решения задач анализа статики в качестве математической модели могут быть использованы системы линейных алгебраических уравнений, которые могут быть представлены в обычной или матричной форме. Для решения задач анализа переходных процессов используются обыкновенные дифференциальные уравнения.
Анализ частотных характеристик процесса выполняется с использованием обыкновенных дифференциальных уравнений или с помощью математических моделей, представленных в форме передаточных функций W( S) или частотной характеристики W( iω), где ω - частота внутренних колебаний системы; i - мнимая единица;  - комплексная переменная. Передаточная функция представляет собой отношение выходной величины Y( S) к входной величине X( S), преобразованных по Лапласу. Частотная характеристика представляет собой отношение тех же величин амплитуд вынужденных колебаний) Y( iω) и X( iω), преобразованных по Фурье.
- комплексная переменная. Передаточная функция представляет собой отношение выходной величины Y( S) к входной величине X( S), преобразованных по Лапласу. Частотная характеристика представляет собой отношение тех же величин амплитуд вынужденных колебаний) Y( iω) и X( iω), преобразованных по Фурье.
При использовании обыкновенных дифференциальных уравнений свойства объекта исследуются во временной области, при использовании передаточных функций свойства объекта исследуются в комплексной области, а при использовании частотных характеристик свойства объекта исследуются в частотной области.
|
|
|
Устойчивость (или стабильность) системы характеризует такое поведение системы, при котором ее движение, начавшись внутри некоторого фазового пространства, никогда его не покидает. Простейшим случаем устойчивого состояния системы является равновесие. Условия устойчивости могут определяться различными критериями.
При многовариантном анализе решение системы тех же уравнений многократно повторяется при варьировании внутренними и (или) внешними параметрами, т. е, в этом случае свойства системы исследуются для некоторой области пространства состояний. Типовыми процедура многовариантного анализа являются анализ чувствительности и статистический анализ, при котором требуется получить информацию о рассеянии (дисперсии) выходных параметров относительно номинальных значений.
Для анализа чувствительности математической модели, выражаемой дифференциальными уравнениями обычно применяются численные методы, при использовании которых задаются приращением  входного параметра и определяют соответствующее изменение
входного параметра и определяют соответствующее изменение 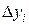 , выходного параметра, после чего определяется коэффициент чувствительности
, выходного параметра, после чего определяется коэффициент чувствительности 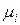 :
:
 . (5.2)
. (5.2)
|
|
|
Пользователь по своему усмотрению с учетом программных возможностей ЭВМ для реализации математической модели, описывающей свойства проектируемого объекта, может использовать различные численные методы решения уравнений. При этом, однако, нужно принимать во внимание эффективность метода, которая характеризуется:
экономичностью, т. е. затратами вычислительных ресурсов ЭВМ (машинного времени и машинной памяти) на применение метода;
надежностью, которая оценивается как вероятность получения правильных результатов при использовании метода для решения данного класса задач;
точностью результатов, получаемых при использовании метода; определяемая погрешность решения задачи не должна превышать допустимые пределы.
Проектные процедуры синтеза. Проектные процедуры синтеза к построению структуры объекта, например, разработка кинематической схемы машины или механизма, и определению параметров объекта, которые обеспечить заданные условия его функционирования.
Если задачи анализа с оценкой проектных решений, то задачи синтеза связаны с нахождением проектных решений в виде описания проектируемого объекта.
Процедуры синтеза делятся на процедуры структурного и параметрического синтеза. Целью структурного синтеза является определение структуры объекта (набора составляющих его элементов и связей между ними) при известных параметрах объекта. Целью параметрического синтеза является определение числовых значений параметров элементов объекта при известной его структуре.
|
|
|
На рисунке 5.2 указаны некоторые классы задач, которые решаются при анализе и синтезе объектов проектирования.
Процедуры оптимизации. При проектировании любых технических объектов оптимизация структуры объекта и его параметров является одной из наиболее важных задач, решаемых в ходе проектирования.
Получение оптимальных решений при проектировании связано с постановкой оптимизационных задач и применением различных методов их решения. В зависимости от характера и назначения проектируемого объекта и требований технического задания (ТЗ) выбирается критерий оптимальности или формируется целевая функция, определяются ограничения, накладываемые на решение задачи (такие ограничения могут быть связаны с производственными возможностями, с требованиями стандартизации, с физическими принципами, положенными в основу функционирования объекта).
|
|
|
После этого формируется математическая модель оптимизационной задачи, в которой критерий оптимальности и величины, на которые накладываются ограничения, выражены в функции независимых переменных проектирования, которые и подлежат определению.
В задачах оптимизации, в которых ограничения имеют вид уравнений, количество ограничений п не может быть больше числа переменных т.е. п<т. Разность (т-п) определяет число степеней свободы в данной задаче. Только (т-п) переменных берутся произвольными и их значения определяются из условия достижения критерием оптимальности экстремального значения; значения же остальных переменных находятся из системы ограничений, определяя допустимую область решений.
Если т = п, то число степеней свободы равно нулю и задача в этом случае становится чисто алгебраической, в которой все переменные определяются из уравнений, а оптимизация целевой функции не требуется (свободные переменные отсутствуют).
Таким образом, математически формализованная задача оптимизации должна содержать:
перечень переменных проектирования, т. е. параметров, значения которых должны быть определены в ходе решения задачи, а также допустимую область изменения этих параметров;
нормативные (директивные) параметры, значения которых задаются однозначно или множеством (массивом) возможных значений;
математическую модель, содержащую связи переменных проектируемого объекта друг с другом и с нормативными параметрами.
Удовлетворение этим связям свидетельствует о выполнении условия непротиворечивости значений переменных проектирования друг другу и нормативным параметрам. Эти условия являются обязательными при оптимальном проектировании.
С учетом математической постановки задачи и математической модели, положенной в ее основу, выбирается тот или иной метод ее решения.
Лекция 8
Тема: Математическое моделирование объектов проектирования. Основные понятия и определения (2 ч.)
План лекции: Математическое моделирование и основные определения. Некоторые виды представления математических моделей объектов проектирования. Особенности построения математических моделей сложных объектов
8.1 Математическое моделирование и основные определения
Любое количественное изучение процесса возможно лишь в том случае, если определены те величины, которые характеризуют его с количественной точки зрения. Каждое мгновенное состояние системы, соответствующее некоторому фиксированному моменту времени, описывается набором чисел, например а1,а2,.,.,ап, которые называются параметрамисистемы. Если процесс рассматривается как последовательная смена состояний системы во времени t, то величины al ( t), a2( t),.., an( t) оказываются функциями времени t. Величины вида al ( t), a2( t),.., an( t), описывающие процесс функционирования системы, называются характеристикамипроцесса. Величины, определяющие начальное состояние системы, называются начальными условиями.
Под математической моделью реальной системы (процесса) понимается совокупность соотношений (имеющих, например, форму уравнений, неравенств, логических условий и т.д.), которые связывают характеристики процесса с параметрами соответствующей системы, исходными данными и начальными условиями.
Таким образом, математическая модель, это некоторый условный (формализованный) образ объекта (системы), поставленный в соответствие данному реальному (физическому) объекту. Процесс исследования объектов на математических моделях называется математическим моделированием.
Метод математического моделирования включает все действия, связанные с предварительным изучением объекта, выделением его наиболее существенных характеристик, экспериментальным определением численных значений параметров объекта, включаемых в математическую модель, с построением самой модели и, наконец, с ее реализацией на ЭВМ и анализом полученных результатов.
Построение математической модели является одной из наиболее ответственных и сложных фаз моделирования. Построение модели всегда влечет немало вопросов, например, такие:
1. Грамотно ли с математической точки зрения составлена система соотношений, образующих математическую модель?
2. Имеет ли эта система решение и если имеет, то единственно ли оно? (Если задача состоит в нахождении решения 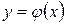 , где x – исходные данные задачи, y – ее решение, φ – функциональная связь между x и y, то такая задача считается корректно поставленной, когда решение задачи а) существует; б) единственно; в) устойчиво по отношению к возмущениям).
, где x – исходные данные задачи, y – ее решение, φ – функциональная связь между x и y, то такая задача считается корректно поставленной, когда решение задачи а) существует; б) единственно; в) устойчиво по отношению к возмущениям).
3. Можно ли указать точнее аналитическое решение задачи для каких-то частных случаев? (Это очень важно при исследовании сложных систем, расчет которых проводится численными методами. Проведя для таких систем численный расчет и сравнив результаты с аналитическим решением, можно судить, во-первых, о правильности выбранного метода расчета и, во-вторых, аналитические, хотя и более грубое решение задачи, позволяет лучше выявить связи между входными и выходными величинами системы и учесть их при построении общего алгоритма задачи).)
4. Нельзя ли ради того, чтобы решить полученные уравнения более простыми методами, как-то упростить их, например, опустив тот или иной член?
При этом надо иметь ввиду, что такое упрощение равносильно некоторому допущению о характере исследуемой системы и, следовательно, принимая его мы очерчиваем границы применимости математической модели. Очевидно, что результаты решения задачи на такой модели нельзя распространять за эти границы.
Существенное значение при построении математических моделей имеет выбор математического аппарата. Например, в задачах статики обычно используются алгебраические уравнения, в задачах динамики механических систем - дифференциальные уравнения (обыкновенные или с частными производными), при исследовании стохастических систем - аппарат теории вероятностей и методы статистического моделирования.
Построив математическую модель, нужно проверить её на адекватность, чувствительность и устойчивость.
Адекватность модели определяется точностью совпадения выходных параметров модели и объекта, описываемого этой моделью. Если 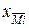 значение выходного i-го параметра,
значение выходного i-го параметра, 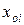 - значение того же i-го параметра объекта, то относительная погрешность
- значение того же i-го параметра объекта, то относительная погрешность
 . (8.1)
. (8.1)
Погрешность модели  по совокупности учитываемых т параметров
по совокупности учитываемых т параметров


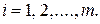 (8.2)
(8.2)
При заданной допустимой погрешности 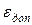 должно выполняться
должно выполняться
условие 
Чувствительность модели характеризует, как изменяются выходные параметры модели при различных вариациях входных параметров.
Устойчивость модели определяет, насколько изменяется выходная величина при изменении входной величины, вызванным погрешностью измерений или упрощением соотношений, входящих в математическую модель.
Правильно построенная и удовлетворяющая указанным требованиям математическая модель позволяет не только описать поведение и свойства объекта в данной конкретной ситуации, но и предсказать, как объект будет себявести в данных условиях при изменении его параметров.
Один и тот же объект может описываться различными моделями, отличающимися как используемым математическим аппаратом, так и степенью детализации описываемых свойств объекта, набором учитываемых параметров и характеристик.
8.2 Некоторые виды представления математических моделей объектов проектирования
Проиллюстрируем построение математической модели объекта на следующем простом примере.
Пусть груз, масса которого равна т, колеблется на упругой опоре (например, на рессорной подвеске), жёсткость которой равна с (здесь т и с - параметры рассматриваемой системы). При этом со стороны опоры на груз действует сила упругости
 (8.3)
(8.3)
где  -отклонение центра масс груза от положения равновесия в момент времени t.
-отклонение центра масс груза от положения равновесия в момент времени t.
В соответствии со вторым законом Ньютона произведение массы груза т на его ускорение.j равно действующей на груз силе, т. е.
F = mj, (8.4)
где
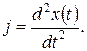 (8.5)
(8.5)
Из сопоставления выражений (8.3), (8.4) и (8.5) следует
 (8.6)
(8.6)
Разделив обе части уравнения (8.6) на т и обозначив
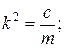
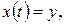 (8.7)
(8.7)
получим
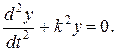 (8.8)
(8.8)
Уравнение (8.8) представляет собой знакомую из механики запись уравнения свободных колебаний системы.
Решая это уравнение для начальных условий
при 
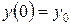 ;
; 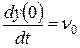 , получим
, получим
 (8.10)
(8.10)
 (8.11)
(8.11)
Как видим, здесь характеристики системы у = x( t) и 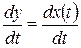 выражены через её параметры т и с
выражены через её параметры т и с  и начальные условия (
и начальные условия ( 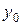 и
и  ) и в силу этого уравнения (8.10) и (8.11) представляют собой математическую модель данной системы.
) и в силу этого уравнения (8.10) и (8.11) представляют собой математическую модель данной системы.
Но в качестве математической модели может быть принята и исходная модель, составленная из первоначальных соотношений (8.3), (8.4) и (8.5) или уравнение (8.6), полученное путем преобразования исходной модели к виду, удобному для интегрирования.
8.3 Особенности построения математических моделей
сложных объектов
При моделировании относительно сложных систем (или процессов) систему можно расчленить на отдельные подсистемы (подпроцессы) и для каждой из них выбрать характеристики 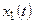 ,
,  ,
,  ,…,
,…, 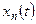 , а вкачестве параметров -некоторые величины d1, d2, ..., dk. Bэтом случае математическая модель системы (процесса) может быть записана в виде системы соотношений:
, а вкачестве параметров -некоторые величины d1, d2, ..., dk. Bэтом случае математическая модель системы (процесса) может быть записана в виде системы соотношений:
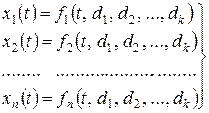 (8.12)
(8.12)
Однако, для того, чтобы такая математическая модель могла быть реализована, необходимо, чтобы функции f1, f2,…, fn были известны (хотя бы приближённо). Но на практике модели такого вида, когда характеристики системы являются явными функциями от ее параметров и времени, встречаются весьма редко и также редки случаи, когда сложная система может быть описана соотношениями типа (8.12).
Дата добавления: 2021-04-15; просмотров: 42; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
