Доказательство некоторых аксиом на основе определений точки, прямой и плоскости. Доказательство 5-го постулата Евклида
Большинство аксиом геометрии (как они изложены, например, у Гильберта) являются по существу неявными определениями точки, прямой и плоскости. Естественно, что при явном определении основных понятий прежние аксиомы становятся следствием этих определений.
Покажем, к примеру, как доказывается утверждение о том, что прямая является кратчайшей линией между двумя заданными точками А и В.
Уясним сначала, как получить кратчайшую линию. Если мы будем подбирать такой раствор циркуля, чтобы проведенные им окружности a и b с центрами в точках А и В касались друг друга внешними сторонами, то точка касания С, очевидно, будет принадлежать кратчайшей линии (см. рис.2).
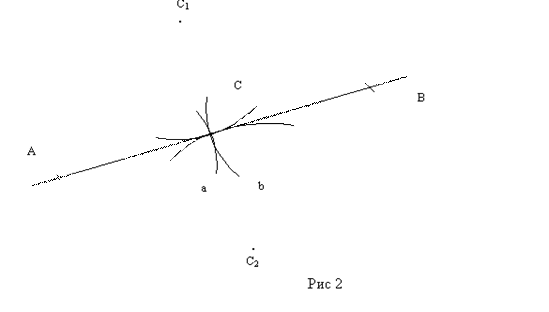
С другой стороны, если мы будем строить прямую через точки A и B как линию, равноотстоящую от дуг с центрами в C1 и C2, кривизна которых равна по величине, но противоположна по знаку, то убедимся, что ввиду полной симметрии эта прямая проходит через С. Повторяя этот процесс со вновь построенной и исходными точками получим требуемый результат.
Теперь мы можем уточнить термин “расстояние”. Под этим термином понимается положительное число, показывающее, сколько раз выбранный нами в качестве единицы измерения раствор циркуля уложится вдоль кратчайшей линии (Мы не останавливаемся на технических деталях измерения дробной части).
Отметим, что в некоторых учебниках вводится такое понимание слова “между”: “Если точка C находится между точками A и B, то точка C принадлежит прямой AB”. В общепринятом языке предлог “между” употребляется для любой линии, а не только для прямой. При дальнейшем изложении авторам этих учебников постоянно приходится напоминать об этом вряд ли оправданном ограничении.
|
|
|
Покажем, в качестве 2-го примера, как можно доказать предложение, эквивалентное 5-му постулату Евклида:
Плоская эквидистантная линия (ЭЛ) прямой есть прямая и притом перпендикулярная перпендикуляру исходной прямой (ИП).
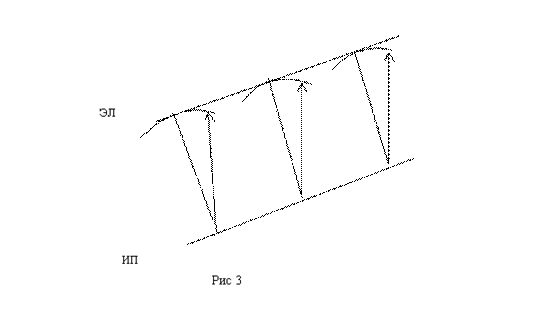
Для построения ЭЛ необходимо строить перпендикуляры к ИП (см. рис. 3) и циркулем откладывать на них заданное расстояние R, т.е., на каждом перпендикуляре строить окружность. ЭЛ не может содержать больше одной общей точки с этой окружностью, т.к., если бы она содержала еще точку, то, проведя из нее на ИП перпендикуляр, мы получили бы, что длина полухорды, не проходящей через центр, равна длине радиуса (требование эквидистантности), что невозможно. Поэтому ЭЛ должна быть внешней касательной к этой окружности и, следовательно, она ортогональна к перпендикуляру ИП. Если мы попытаемся провести через любые три точки ЭЛ окружность, то убедимся, что это невозможно, т.к. центр искомой окружности должен находится на пересечении прямых, ортогональных участкам ЭЛ, т.е. — на перпендикулярах к ИП, а эти перпендикуляры не пересекаются. Следовательно, ЭЛ даже на малом участке не может быть частью окружности конечного радиуса, а значит и вообще — какой-либо кривой. Единственным непротиворечивым вариантом остается, что ЭЛ — прямая, перпендикулярная перпендикуляру ИП.
|
|
|
То, что однородность и изотропность пространства неминуемо приводит к 5-му постулату Евклида, не является новостью, однако исторически сложилось, что длительное время, а во многих учебниках и сейчас, эта взаимосвязь остается в тени. Между тем исключение 5-го постулата из ОГ делает геометрию неопределенной. Ввод же предложений, альтернативных этому постулату, требует определения законов, по которым меняется метрика пространства. Формулируя эти законы, конструкторы неевклидовых геометрий неминуемо, явно или неявно, все изменения размеров циркуля отсчитывают от его первоначального раствора, т.е., используют понятия евклидовой геометрии. Поэтому Евклидова геометрия не просто одна из многих и даже не первая среди равных, а, в сущности, она является единственной основой всех геометрических построений, не теряющих, разумеется, своей полезности оттого, что могут быть сформулированы в рамках единой науки.
|
|
|
Не исключено, что у читателя могут появиться замечания к строгости приведенных доказательств, но тем и хорош метод рекурсии, что всегда можно вернуться к прежним доказательствам и высветить их более острым лучом новых знаний – важно лишь, чтобы эти доказательства не составляли замкнутого круга и, естественно, были не противоречивы. Можно смело утверждать, что метод рекурсии позволит не только доказать все аксиомы, но и улучшить доказательство других теорем, при этом нет никакой необходимости с самого начала “нагружать” малышей бессмысленными с их точки зрения абстрактными понятиями в угоду строгой иерархии.
Мы еще вернемся к вопросам о пространстве, а сейчас остановимся на проблемах, связанных со 2-м законом термодинамики.
Дата добавления: 2021-07-19; просмотров: 109; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
