Предваренная нормальная форма.
Пример 2. Привести к ПНФ следующую предикатную формулу.
ù($x"yР1(х,y) & $х"y v P2(х,,y)).
Поскольку в данной предикатной формуле имеются два высказывания $х"уР1(х,у) и , $х"уР2(х,у) объединенные связкой & и общим отрицанием ~|, то, применив правило де
Моргана (5.17) к исходной формуле, получим:
ù$х"уР1(х,у) & $х"уР2(х,у))
~ ù$х"уР1(х,у) v $х"уР2(х,у))
Воспользуемся далее эквивалентным соотношение (5.3):
ù$х"уР1(х,у) & $х"уР2(х,у))
~ ù$х"уР1(х,у) v $х"уР2(х,у))
Продолжая перемещение символов отрицания непосред-
ственно к символам предикатов, используем соотношение (5.4):
"хù "у Р (х,у) v "хù $у Р2 (х, у) ~
~ "хù "у Р (х,у) v "х ù "у Р2 (х, у)
Так как квантор общности Ух не дистрибутивен относительно дизъюнкции v, поменяем в каком-либо предикате,например во втором, переменную х на новую переменную г:
"х $уù Р (х,у) v "х $у ùР2 (х, у) ~
"х $уù Р (х,у) v "z $у ùР2 (z, у) ~
Воспользовавшись дважды эквивалентным соотношением (5.10) или соотношением (5.21), получим:
"х $уù Р (х,у) v "z $у ùР2 (z, у) ~
~ "х "z ($yù Р1 (х, у) v $y Р2 (z, у)).
Поскольку квантор существования $у дистрибутивен относительно дизъюнкции v (см. (5.6)), окончательно получим префиксную нормальную форму для исходной предикатной формулы:
"х"z($y ù Р1(х,y) v $yù Р2(x,y))~
~"х"z$y (ù Р1(х,y) v ù Р2(x,y))
Пример 3. Получить ПНФ предикатной формулы:
|
|
|
"х"у($z(P1(х,z) & P2(у,z)) ®$u Р3(х,у, u)).
Для получения ПНФ удалим из исходной формулы связку→ , используя формулу булевой алгебры (5.14):
"х"у($z(P1(х,z) & P2(у,z)) ®$u Р3(х,у, u)) ~
~"х"у(ù$z(P1(х,z) & P2(у,z)) v $u Р3(х,у, u))
Избавимся от отрицания перед квантором Зг, используя (5.3):
"х"у(ù $z(P1(х,z) & P2(у,z)) v $u Р3(х,у, u)) ~
~ "х"у("zù(P1(х,z) & P2(у,z)) v $u Р3(х,у, u))
Воспользуемся далее правилом де Моргана (5.17):
"х"у("zù(P1(х,z) & P2(у,z)) v $u Р3(х,у, u))~
~ "х"у"z(ù P1(х,z) vù P2(у,z)) v $u Р3(х,у, u))
Так как последний предикат не зависит от переменной 2,
используем соотношение (5.10):
"х"у"z(ù P1(х,z) vù P2(у,z)) v $u Р3(х,у, u)) ~
~ "х"у"z(ù P1(х,z) vù P2(у,z) v Р3(х,у, u))
Аналогично для вынесения квантора зу (благодаря независимости первых предикатов от переменной и) воспользуемся (5.12):
"х"у"z(ù P1(х,z) vù P2(у,z)) v $u Р3(х,у, u)) ~
~ "х"у"z$u(ù P1(х,z) vù P2(у,z) v Р3(х,у, u))
Полученная в результате выполненных эквивалентных преобразований формула является ПНФ исходной формулы.
Пример 4. Получить ПНФ предикатной формулы
(ù $u Р1(u) ® ù "у "u Р2(у,u)) ® "х Р3(х).
Для получения ПНФ осуществим эквивалентные преобразования, указывая каждый раз справа номер используемого эквивалентного соотношения:
|
|
|
(ù $u Р1(u) ® ù "у "u Р2(у,u)) ® "х Р3(х)~ по (5.14)
~ (ùù $u Р1(u) v ù "у "u Р2(у,u)) ® "х Р3(х)~ по (5.15)
~ ($u Р1(u) v ù "у "u Р2(у,u)) ® "х Р3(х)~ по (5.14)
~ù($u Р1(u) v ù "у "u Р2(у,u)) v "х Р3(х) ~ по (5.16)
~ (ù $u Р1(u) & ùù "у "u Р2(у,u)) v "х Р3(х)~ по(5.15)
~ (ù $u Р1(u) & "у "u Р2(у,u)) v "х Р3(х)~ по (5.3)
~ ("u ù Р1(u) & "у "u Р2(у,u)) v "х Р3(х)~ по (5.5)
~ "u (ù Р1(u) & "у Р2(у,u)) v "х Р3(х)~ по (5.9)
~ "u "y(ù Р1(u) & Р2(у,u)) v "х Р3(х)~ по (5.10)
~ "u "y "x(ù Р1(u) & Р2(у,u) v Р3(х))~ по (5.7)
~ "x "y "u(ù Р1(u) & Р2(у,u) v Р3(х))~
2. Получить ПНФ следующих предикатных формул:
а) $x"yP1(x,y)®"x$yP2(x,y);
б) ($x"yP1(x,y) Ú $xP2(x))®$y"zP3(y,z);
в) ù ($x"zP1(x,z)®$y$zP2(y,z)) & ù $y $z P3(y,z)
г) ($x"zP1(x,z) Ú ù"x"yP2(x,y))®ù"zP3(z);
д) ("x$y"zP1(x,y,z) Ú ù"yP2(x,y))®"x"zP3(x,z);
е) ù ("x"y"zù P1(x,y,z) Ú $y$zP2(y,z))&"x"zP3(x,z);
ж) ("x"y P1(x,y) ® $x$y"zP2(x,y,z))®$zP3(z);
з) ù"x$y P1(x,y) ® ("y"zP2(y,z))®ù "zP3(z));
и) (ù $y P1(y) ®ù "x"yP2(x,y))®"zP3(z);
к) ù ("x"y P1(x,y) Ú "x$yP2(x,y,)).
8.3 Домашнее задание
1. На множестве М = {1,2,3,...,20} заданы предикаты:
|
|
|
А(х): «х не делится на 5»;
В(х): «x - четное число»;
С(x): «x - число простое»;
D(x): «x кратно 3».
Найдите множества истинности следующих предикатов:
11)  12)
12) 
13) 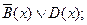 14)
14) 
9 Занятие №9
9.1 Графы
Определение графа
Графом  называется пара
называется пара 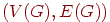 , где
, где  — непустое конечное множество элементов, называемых вершинами, а
— непустое конечное множество элементов, называемых вершинами, а  — конечное семейство неупорядоченных пар элементов из
— конечное семейство неупорядоченных пар элементов из  (необязательно различных), называемых ребрами. Употребление слова "семейство" говорит о том, что допускаются кратные ребра. Будем называть
(необязательно различных), называемых ребрами. Употребление слова "семейство" говорит о том, что допускаются кратные ребра. Будем называть  "множеством вершин" , а
"множеством вершин" , а  — семейством ребер графа
— семейством ребер графа  . О каждом ребре вида
. О каждом ребре вида  говорят, что оно соединяет вершины
говорят, что оно соединяет вершины  и
и  . Каждая петля
. Каждая петля  соединяет вершину
соединяет вершину  саму с собой.
саму с собой.
При изображении графов на рисунках или схемах отрезки могут быть прямолинейными или криволинейными; длины отрезков и расположение точек произвольны.
Определение орграфа
Орграфом  называется пара
называется пара  , где
, где  — непустое конечное множество элементов, называемых вершинами , а
— непустое конечное множество элементов, называемых вершинами , а  — конечное семейство упорядоченных пар элементов из
— конечное семейство упорядоченных пар элементов из  , называемых дугами (или ориентированными ребрами). Дуга, у которой вершина
, называемых дугами (или ориентированными ребрами). Дуга, у которой вершина  является первым элементом, а вершина
является первым элементом, а вершина  — вторым, называется дугой из
— вторым, называется дугой из  в
в 
 . Заметим, что дуги
. Заметим, что дуги  и
и  различны. Хотя графы и орграфы — существенно различные объекты, в определенных случаях графы можно рассматривать как орграфы, в которых каждому ребру соответствуют две противоположно ориентированные дуги.
различны. Хотя графы и орграфы — существенно различные объекты, в определенных случаях графы можно рассматривать как орграфы, в которых каждому ребру соответствуют две противоположно ориентированные дуги.
|
|
|
Полный граф
Граф называется полным, если каждые две различные вершины его соединены одним и только одним ребром. В полном графе каждая его вершина принадлежит одному и тому же числу ребер. Для задания полного графа достаточно знать число его вершин. Полный граф с  вершинами обычно обозначается через
вершинами обычно обозначается через 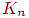 .
.
Граф, не являющийся полным, можно преобразовать в полный с теми же вершинами, добавив недостающие ребра. Вершины графа  и ребра, которые добавлены, тоже образуют граф. Такой граф называют дополнением графа
и ребра, которые добавлены, тоже образуют граф. Такой граф называют дополнением графа  и обозначают его
и обозначают его  .
.
Дополнением графа  называется граф
называется граф  с теми же вершинами, что и граф
с теми же вершинами, что и граф  , и с теми и только теми ребрами, которые необходимо добавить к графу
, и с теми и только теми ребрами, которые необходимо добавить к графу  , чтобы получился полный граф.
, чтобы получился полный граф.
Является граф полным или нет, это его характеристика в целом.
Полный ориентированный граф
Полным ориентированным графом называется граф, каждая пара вершин которого соединена в точности одним ориентированным ребром. Если с каждого ребра полного ориентированного графа снять направление, то образуется полный граф с неориентированными ребрами.
Рассмотрим соревнование, в котором каждая из команд играет с каждой из остальных команд по одному разу. Такое соревнование называют круговым турниром или турниром в один круг.
Если каждая встреча непременно должна оканчиваться выигрышем одной из команд, то круговой турнир называют бескомпромиссным. Круговой бескомпромиссный турнир проводится, например, в волейболе и баскетболе.
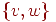
Каждому турниру соответствует полный ориентированный граф, в котором вершины представляют команды, а каждое ориентированное ребро  выражает отношение "
выражает отношение "  победила
победила  ".
".
Двудольный граф
Допустим, что множество вершин графа можно разбить на два непересекающихся подмножества  и
и  , так, что каждое ребро в
, так, что каждое ребро в  соединяет какую-нибудь вершину из
соединяет какую-нибудь вершину из  с какой-либо вершиной из
с какой-либо вершиной из  , тогда
, тогда  называем двудольным графом. Такие графы иногда обозначают
называем двудольным графом. Такие графы иногда обозначают 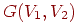 , если хотят выделить два указанных подмножества. Двудольный граф можно определить и по-другому: в терминах раскраски его вершин двумя цветами, скажем, красным и синим. При этом граф называется двудольным, если каждую его вершину можно окрасить красным или синим цветом так, чтобы любое ребро имело один конец красный, а другой — синий. Следует подчеркнуть, что в двудольном графе совсем не обязательно каждая вершина из
, если хотят выделить два указанных подмножества. Двудольный граф можно определить и по-другому: в терминах раскраски его вершин двумя цветами, скажем, красным и синим. При этом граф называется двудольным, если каждую его вершину можно окрасить красным или синим цветом так, чтобы любое ребро имело один конец красный, а другой — синий. Следует подчеркнуть, что в двудольном графе совсем не обязательно каждая вершина из  соединена с каждой вершиной из
соединена с каждой вершиной из  ; если же это так и если при этом граф
; если же это так и если при этом граф  простой, то он называется полным двудольным графом и обычно обозначается
простой, то он называется полным двудольным графом и обычно обозначается  , где
, где  — число вершин соответственно в
— число вершин соответственно в  и
и  .
.
Пример.

Заметим, что граф  имеет ровно
имеет ровно  вершин и
вершин и  ребер.
ребер.
Степень вершины
Вершины в графе могут отличаться друг от друга тем, скольким ребрам они принадлежат.
Степенью вершины называется число ребер графа, которым принадлежит эта вершина. Вершина называется четной, если ее степень — число четное. Вершина называется нечетной, если ее степень — число нечетное. Две вершины графа называются смежными, если существует соединяющее их ребро, то есть ребро вида  ; при этом вершины
; при этом вершины  и
и  называются инцидентными этому ребру, а ребро — инцидентным этим вершинам. Аналогично, два различных ребра графа называются смежными, если они имеют, по крайней мере, одну общую вершину. Иначе можно определить степень вершины. Степенью или валентностью вершины
называются инцидентными этому ребру, а ребро — инцидентным этим вершинам. Аналогично, два различных ребра графа называются смежными, если они имеют, по крайней мере, одну общую вершину. Иначе можно определить степень вершины. Степенью или валентностью вершины  графа
графа  называется число ребер, инцидентных
называется число ребер, инцидентных  ; степень вершины будем обозначать через
; степень вершины будем обозначать через  . При вычислении степени вершины
. При вычислении степени вершины  будем учитывать петлю в
будем учитывать петлю в  два раза, а не один. Вершина степени
два раза, а не один. Вершина степени  называется изолированной вершиной, вершина степени
называется изолированной вершиной, вершина степени  называется висячей, или концевой, вершиной. Граф, у которого все вершины имеют одну и ту же степень, называется регулярным графом.
называется висячей, или концевой, вершиной. Граф, у которого все вершины имеют одну и ту же степень, называется регулярным графом.
Два графа, 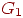 и
и  , называются изоморфными, если существует взаимно однозначное соответствие между множествами их вершин, обладающее тем свойством, что число ребер, соединяющих любые две вершины в
, называются изоморфными, если существует взаимно однозначное соответствие между множествами их вершин, обладающее тем свойством, что число ребер, соединяющих любые две вершины в 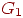 равно числу ребер, соединяющих соответствующие вершины в
равно числу ребер, соединяющих соответствующие вершины в  .
.
Имея даже общие представления о графе, иногда можно судить о степенях его вершин. Так, степень каждой вершины полного графа на единицу меньше числа его вершин. При этом некоторые закономерности, связанные со степенями вершин, присущи не только полным графам.
1. В графе  сумма степеней всех его вершин — число четное, равное удвоенному числу ребер графа, так как каждое ребро участвует в этой сумме ровно два раза. Этот результат, известный еще двести лет назад Эйлеру, часто называют леммой о рукопожатиях. Из нее следует, что если несколько человек обменялись рукопожатиями, то общее число пожатых рук обязательно четно, ибо в каждом рукопожатии участвуют две руки (при этом каждая рука считается столько раз, сколько она участвовала в рукопожатиях).
сумма степеней всех его вершин — число четное, равное удвоенному числу ребер графа, так как каждое ребро участвует в этой сумме ровно два раза. Этот результат, известный еще двести лет назад Эйлеру, часто называют леммой о рукопожатиях. Из нее следует, что если несколько человек обменялись рукопожатиями, то общее число пожатых рук обязательно четно, ибо в каждом рукопожатии участвуют две руки (при этом каждая рука считается столько раз, сколько она участвовала в рукопожатиях).
2. Число нечетных вершин любого графа четно.
3. Во всяком графе с  вершинами, где
вершинами, где  , всегда найдутся по меньшей мере две вершины с одинаковыми степенями.
, всегда найдутся по меньшей мере две вершины с одинаковыми степенями.
4. Если в графе с вершинами  в точности две вершины имеют одинаковую степень, то в этом графе всегда найдется либо в точности одна вершина степени
в точности две вершины имеют одинаковую степень, то в этом графе всегда найдется либо в точности одна вершина степени  , либо в точности одна вершина степени
, либо в точности одна вершина степени  .
.
Начало формы
Вы можете поддержать наш проект и автора курса?
Конец формы
Связность графа
Назовем граф связным,если его нельзя представить в виде объединения двух графов, и несвязным — в противном случае.
Маршрутом в данном графе  называется конечная последовательность ребер вида
называется конечная последовательность ребер вида

(обозначаемая также через  ). Очевидно следующее свойство маршрута: любые два последовательных ребра либо смежны, либо одинаковы. Но не всякая последовательность ребер, обладающая этим свойством, является маршрутом (в качестве примера рассмотрим звездный граф и возьмем его ребра в произвольном порядке). Каждому маршруту соответствует последовательность вершин
). Очевидно следующее свойство маршрута: любые два последовательных ребра либо смежны, либо одинаковы. Но не всякая последовательность ребер, обладающая этим свойством, является маршрутом (в качестве примера рассмотрим звездный граф и возьмем его ребра в произвольном порядке). Каждому маршруту соответствует последовательность вершин 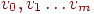 .
.  называется начальной вершиной, а
называется начальной вершиной, а  конечной вершиной маршрута. Таким образом, мы будем говорить о маршруте из
конечной вершиной маршрута. Таким образом, мы будем говорить о маршруте из  в
в  . Заметим, что для любой вершины
. Заметим, что для любой вершины  тривиальным маршрутом, вообще не содержащим ребер, является маршрут из
тривиальным маршрутом, вообще не содержащим ребер, является маршрут из  в
в  . Длиной маршрута называется число ребер в нем. Маршрут называется цепью, если все его ребра различны, и простой цепью, если все вершины
. Длиной маршрута называется число ребер в нем. Маршрут называется цепью, если все его ребра различны, и простой цепью, если все вершины 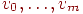 различны, кроме, может быть,
различны, кроме, может быть,  . Замкнутая простая цепь, содержащая по крайней мере одно ребро, называется циклом. В частности, любая петля или любая пара кратных ребер образует цикл. Путь (последовательность ребер, ведущая от
. Замкнутая простая цепь, содержащая по крайней мере одно ребро, называется циклом. В частности, любая петля или любая пара кратных ребер образует цикл. Путь (последовательность ребер, ведущая от  к
к  , в которой каждые два соседних ребра имеют общую вершину и никакое ребро не встречается более одного раза) от вершины
, в которой каждые два соседних ребра имеют общую вершину и никакое ребро не встречается более одного раза) от вершины  до вершины
до вершины  называется простым, если он не проходит ни через одну из вершин графа более одного раза.
называется простым, если он не проходит ни через одну из вершин графа более одного раза.
Граф  называется связным, если для любых двух его вершин
называется связным, если для любых двух его вершин  и
и  существует простая цепь из
существует простая цепь из  в
в  . Любой граф можно разбить на непересекающиеся связные графы, называемые компонентами (связности) графа
. Любой граф можно разбить на непересекающиеся связные графы, называемые компонентами (связности) графа  . Таким образом, несвязный граф имеет, по крайней мере, две компоненты. Две вершины эквивалентны (или связаны, если существует простая цепь из одной в другую.Связный граф состоит из одной компоненты. Граф называется несвязным, если число его компонент больше единицы.
. Таким образом, несвязный граф имеет, по крайней мере, две компоненты. Две вершины эквивалентны (или связаны, если существует простая цепь из одной в другую.Связный граф состоит из одной компоненты. Граф называется несвязным, если число его компонент больше единицы.
Связный граф представляет собой простой цикл тогда и только тогда, когда каждая его вершина имеет степень  .
.
Если  — связный граф и степень каждой его вершины
— связный граф и степень каждой его вершины  , тогда
, тогда  — простой цикл.
— простой цикл.
Из каждой вершины данного графа в любую другую ведет путь. Начнем путь из какой-нибудь вершины е и пройдем по одному из двух ребер, которым принадлежит эта вершина. Попав во вторую вершину, выйдем из нее по второму ребру и так далее. С необходимостью все ребра графа будут пройдены, и мы вернемся в исходную вершину.
Если граф  — простой цикл, тогда степень каждой вершины равна двум.
— простой цикл, тогда степень каждой вершины равна двум.
Так как граф  — замкнутый простой путь, то из каждой его вершины можно попасть в любую другую, не проходя ни через одну вершину более одного раза. Степень каждой вершины такого графа равна двум.
— замкнутый простой путь, то из каждой его вершины можно попасть в любую другую, не проходя ни через одну вершину более одного раза. Степень каждой вершины такого графа равна двум.
Покажем, что в простом цикле не может быть вершины, степень которой не равна двум.
Если какая-то вершина в графе имеет степень меньше двух, то она не принадлежит никакому простому циклу.
Если какая-то вершина имеет степень больше двух, то никакой простой цикл (по определению) не может содержать все ребра, которым принадлежит эта вершина.
Начало формы
Вы можете поддержать наш проект и автора курса?
Конец формы
Определения и примеры
Матрицей смежности графа  с множеством вершин
с множеством вершин 
 (соответствующей данной нумерации вершин) называется матрица
(соответствующей данной нумерации вершин) называется матрица  размера
размера  , в которой элемент
, в которой элемент  равен числу ребер в
равен числу ребер в  , соединяющих
, соединяющих  и
и 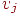 . Можно получить несколько различных матриц смежности данного графа, меняя обозначения его вершин. Это приведет к изменению порядка строк и столбцов матрицы
. Можно получить несколько различных матриц смежности данного графа, меняя обозначения его вершин. Это приведет к изменению порядка строк и столбцов матрицы  . Но в результате всегда получится симметричная матрица из неотрицательных целых чисел, обладающая тем свойством, что сумма чисел в любой строке или столбце равна степени соответствующей вершины. Каждая петля учитывается в степени вершины один раз. Обратно, по любой заданной симметричной матрице из неотрицательных целых чисел легко построить граф, единственный с точностью до изоморфизма, для которого данная матрица является матрицей смежности. Отсюда следует, что теорию графов можно свести к изучению матриц особого типа.
. Но в результате всегда получится симметричная матрица из неотрицательных целых чисел, обладающая тем свойством, что сумма чисел в любой строке или столбце равна степени соответствующей вершины. Каждая петля учитывается в степени вершины один раз. Обратно, по любой заданной симметричной матрице из неотрицательных целых чисел легко построить граф, единственный с точностью до изоморфизма, для которого данная матрица является матрицей смежности. Отсюда следует, что теорию графов можно свести к изучению матриц особого типа.
Матрицей инциденций простого графа с множеством вершин  ,...
,...  называется матрица
называется матрица  размера
размера  , у которой
, у которой  , если вершина
, если вершина 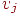 инцидентна ребру
инцидентна ребру  , и
, и  , в противном случае.
, в противном случае.
Граф, у которого множество ребер пусто, называется вполне несвязным или пустым графом. Будем обозначать вполне несвязный граф с  вершинами через
вершинами через  . Простой граф, в котором любые две вершины смежны, называется полным графом. Полный граф с
. Простой граф, в котором любые две вершины смежны, называется полным графом. Полный граф с  вершинами обычно обозначается через
вершинами обычно обозначается через 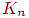 . Граф, у которого все вершины имеют одну и ту же степень, называется регулярным графом. Если степень каждой вершины равна
. Граф, у которого все вершины имеют одну и ту же степень, называется регулярным графом. Если степень каждой вершины равна  , то граф называется регулярным степени
, то граф называется регулярным степени  . Регулярные графы степени 3 называются также кубическими, или трехвалентными графами. Каждый вполне несвязный граф является регулярным степени
. Регулярные графы степени 3 называются также кубическими, или трехвалентными графами. Каждый вполне несвязный граф является регулярным степени  , а каждый полный граф
, а каждый полный граф 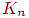 — регулярным степени
— регулярным степени  . Среди регулярных графов особенно интересны платоновы графы — графы, образованные вершинами и ребрами пяти правильных многогранников — платоновых тел: тетраэдра, куба, октаэдра, додекаэдра и икосаэдра.
. Среди регулярных графов особенно интересны платоновы графы — графы, образованные вершинами и ребрами пяти правильных многогранников — платоновых тел: тетраэдра, куба, октаэдра, додекаэдра и икосаэдра.
Объединение и соединение двух графов. Существует несколько способов соединения двух графов для образования нового, большего графа. Рассмотрим два из них. Пусть даны два графа  ,
,  , причем множества
, причем множества 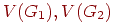 не пересекаются. Тогда объединением
не пересекаются. Тогда объединением  графов
графов  называется граф с множеством вершин
называется граф с множеством вершин  и семейством ребер
и семейством ребер  Можно также образовать соединение графов
Можно также образовать соединение графов  , обозначаемое
, обозначаемое  , взяв их объединение и соединив ребрами каждую вершину графа
, взяв их объединение и соединив ребрами каждую вершину графа 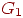 с каждой вершиной графа
с каждой вершиной графа  .
.
Пример матрицы смежности. Пусть дан граф

Матрица смежности

Обхватом графа называется длина его кратчайшего цикла. Множество 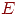 ребер графа называется независимым, если оно не содержит циклов, то есть никакая совокупность ребер из
ребер графа называется независимым, если оно не содержит циклов, то есть никакая совокупность ребер из 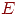 не образует цикла. Диаметром
не образует цикла. Диаметром 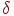 связного графа
связного графа  называется максимальное возможное расстояние между любыми двумя его вершинами. Центром графа
называется максимальное возможное расстояние между любыми двумя его вершинами. Центром графа  называется такая вершина
называется такая вершина  , что максимальное расстояние между
, что максимальное расстояние между  и любой другой вершиной является наименьшим из всех возможных. Это расстояние называется радиусом
и любой другой вершиной является наименьшим из всех возможных. Это расстояние называется радиусом  . Таким образом,
. Таким образом,

где  — расстояние между
— расстояние между  и
и  .
.
Удаление ребер, мосты
При удалении ребра 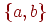 из графа
из графа  получается граф с теми же вершинами, что и граф
получается граф с теми же вершинами, что и граф  , и всеми ребрами, кроме ребра
, и всеми ребрами, кроме ребра 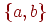 . При удалении ребра из связного графа новый граф может оказаться как связным, так и несвязным. Ребро
. При удалении ребра из связного графа новый граф может оказаться как связным, так и несвязным. Ребро 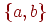 называется мостом графа
называется мостом графа  , если в графе, полученном после удаления из
, если в графе, полученном после удаления из  ребра
ребра 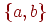 , вершины
, вершины 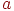 и
и  оказываются несвязными. Существует несколько признаков мостов. Известно, что признак какого-то объекта может заменить его определение, то есть по признаку можно распознать объект. Рассмотрим признаки мостов.
оказываются несвязными. Существует несколько признаков мостов. Известно, что признак какого-то объекта может заменить его определение, то есть по признаку можно распознать объект. Рассмотрим признаки мостов.
Ребро 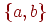 является мостом в том и только в том случае, если
является мостом в том и только в том случае, если 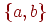 — единственный путь, соединяющий вершины
— единственный путь, соединяющий вершины 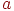 и
и  .
.
Ребро 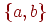 является мостом в том и только в том случае, если найдутся две вершины
является мостом в том и только в том случае, если найдутся две вершины  и
и  , такие, что каждый путь, соединяющий их, содержит
, такие, что каждый путь, соединяющий их, содержит 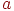 и
и  .
.
Ребро 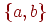 является мостом в том и только в том случае, если оно не принадлежит ни одному циклу.
является мостом в том и только в том случае, если оно не принадлежит ни одному циклу.
Докажем справедливость третьего признака.
Прямая теорема. Если ребро 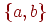 не принадлежит ни одному циклу, то
не принадлежит ни одному циклу, то 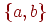 — мост.
— мост.
Так как ребро 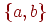 не принадлежит ни одному циклу, при его удалении не останется пути, связывающего
не принадлежит ни одному циклу, при его удалении не останется пути, связывающего 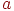 и
и  , то есть
, то есть 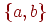 является мостом.
является мостом.
Обратная теорема. Если ребро 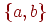 — мост, то
— мост, то 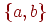 не принадлежит ни одному циклу.
не принадлежит ни одному циклу.
Если бы ребро 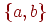 принадлежало циклу, то при удалении ребра
принадлежало циклу, то при удалении ребра 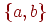 остался бы второй путь, связывающий
остался бы второй путь, связывающий 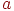 и
и  , то есть ребро
, то есть ребро 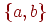 не было бы мостом. Следовательно,
не было бы мостом. Следовательно, 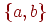 не принадлежит циклу.
не принадлежит циклу.
Деревья
Связные графы, в которых существует одна и только одна цепь, соединяющая каждую пару вершин, называются деревьями. Дерево можно определить и как связный граф, не содержащий циклов.
Пример. Кубок по настольному теннису разыгрывается по олимпийской системе. Встречи проводятся без "ничьих". К очередному туру допускается только победившая в предыдущем туре команда. Проигравшие команды выбывают из игры. Для завоевания кубка команда должна победить во всех турах. На участие в розыгрыше кубка поданы заявки от 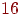 команд.
команд.
Схема проведения игр изображается графом

Вершины нижнего "яруса" дерева интерпретируем как команды, участвующие в розыгрыше кубка, вершины второго снизу яруса — как команды-победительницы в  финала, вершины третьего яруса — как команды-победительницы в
финала, вершины третьего яруса — как команды-победительницы в  финала и т.д.
финала и т.д.
Какую информацию можно получить с помощью этого дерева?
Непосредственно с него считываются:
Число всех участников розыгрыша кубка (число вершин нижнего "яруса").
Число этапов проведения розыгрыша (число "ярусов" из вершин в дереве, не считая нижнего).
Число команд, участвующих в  финала, в
финала, в  финала, в
финала, в  финала (число вершин, соответственно, в четвертом сверху ярусе, в третьем сверху ярусе, во втором сверху ярусе).
финала (число вершин, соответственно, в четвертом сверху ярусе, в третьем сверху ярусе, во втором сверху ярусе).
Число матчей, которые придется сыграть командам для выявления обладателя кубка (число вершин в графе без нижнего "яруса"). Хотя это число легко определяется и без дерева. (В каждом матче выбывает одна команда. Для того чтобы была выявлена команда-победительница, остальные должны выбыть из соревнования. Поэтому число матчей равно числу команд без одной, а именно 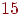 ).
).
Удобно считать, что граф, состоящий из одной изолированной вершины, тоже является деревом. Для каждой пары вершин дерева существует единственный соединяющий их путь. Лесом называется несвязный граф, представляющий объединение деревьев. Всякое ребро в дереве и в лесе является мостом (признак 3).
Пример.
Изображен лес, состоящий из четырех компонент, каждая из которых является деревом.

Заметим, что по определению деревья и леса являются простыми графами. По многим показателям дерево представляет собой простейший нетривиальный тип графа.
Известно, что в связном графе  удаление одного ребра, принадлежащего некоторому выбранному циклу, не нарушает связности оставшегося графа. Применим эту процедуру к одному из оставшихся циклов, и так до тех пор, пока не останется ни одного цикла. В результате получим дерево, связывающее все вершины графа
удаление одного ребра, принадлежащего некоторому выбранному циклу, не нарушает связности оставшегося графа. Применим эту процедуру к одному из оставшихся циклов, и так до тех пор, пока не останется ни одного цикла. В результате получим дерево, связывающее все вершины графа  , оно называется остовным деревом или остовом , или каркасом графа
, оно называется остовным деревом или остовом , или каркасом графа  .
.
В общем случае обозначим через  произвольный граф с
произвольный граф с  вершинами,
вершинами,  ребрами и
ребрами и 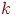 компонентами. Применяя описанную выше процедуру к каждой компоненте
компонентами. Применяя описанную выше процедуру к каждой компоненте  , получим в результате граф, называемый остовным лесом. Число удаленных в этой процедуре ребер называется циклическим рангом или циклическим числом графа
, получим в результате граф, называемый остовным лесом. Число удаленных в этой процедуре ребер называется циклическим рангом или циклическим числом графа  и обозначается через
и обозначается через 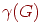 . Мы видим, что
. Мы видим, что  и является неотрицательным целым числом. Таким образом, циклический ранг дает меру связности графа: циклический ранг дерева равен нулю, а циклический ранг циклического графа равен единице. Удобно также определить коциклический ранг или ранг разреза графа
и является неотрицательным целым числом. Таким образом, циклический ранг дает меру связности графа: циклический ранг дерева равен нулю, а циклический ранг циклического графа равен единице. Удобно также определить коциклический ранг или ранг разреза графа  как число ребер в его остовном лесе. Коциклический ранг обозначается через
как число ребер в его остовном лесе. Коциклический ранг обозначается через  и равен
и равен  .
.
10 Занятие №10
10.1 Комбинаторика. Задачи по комбинаторике
1. Расписание одного дня содержит 5 уроков. Определить количество таких расписаний при выборе из одиннадцати дисциплин.
Ответ: 55 440.
2. Комиссия состоит из председателя, его заместителя и еще пяти человек. Сколькими способами члены комиссии могут распределять между собой обязанности?
Ответ: 42.
3. Сколькими способами можно выбрать трех дежурных из группы в 20 человек?
Ответ: 1 140.
4. Сколько различных звукосочетаний можно взять на десяти выбранных клавишах рояля, если каждое звукосочетание может содержать от трех до десяти звуков?
Ответ: 968.
5. В вазе стоят 10 красных и 5 розовых гвоздик. Сколькими способами можно выбрать из вазы пять гвоздик одного цвета?
Ответ: 253.
6. Номера трамвайных маршрутов иногда обозначаются двумя цветными фонарями. Какое количество различных маршрутов можно обозначить, если использовать фонари восьми цветов?
Ответ: 64.
7. Чемпионат, в котором участвуют 16 команд, проводится в два круга (т.е. каждая команда дважды встречается с любой другой). Определить, какое количество встреч следует провести.
Ответ: 240.
8. Замок открывается только в том случае, если набран определенный трехзначный номер. Попытка состоит в том, что набирают наугад три цифры из заданных пяти цифр. Угадать номер удалось только на последней из всех возможных попыток. Сколько попыток предшествовало удачной?
Ответ: 124.
9. Из группы в 15 человек выбирают четырех участников эстафеты 800+400+200+100. Сколькими способами можно расставить спортсменов по этапам эстафеты?
Ответ: 32 760.
10. Команда из пяти человек выступает на соревнованиях по плаванию, в которых участвуют еще 20 спортсменов. Сколькими способами могут распределиться места, занятые членами этой команды?
Ответ: 25!/20!.
11. Сколькими способами можно расположить на шахматной доске две ладьи так, чтобы одна не могла взять другую? (Одна ладья может взять другую, если она находиться с ней на одной горизонтали или на одной вертикали шахматной доски.)
Ответ: 3 126.
12. Две ладьи различного цвета расположены на шахматной доске так, что каждая может взять другую. Сколько существует таких расположений?
Ответ: 896.
13. Порядок выступления восьми участников конкурса определяется жребием. Сколько различных исходов жеребьевки при этом возможно?
Ответ: 8!.
14. Тридцать человек разбиты на три группы по десять человек в каждой. Сколько может быть различных составов групп?
Ответ: 30!/(10!)  .
.
15. Сколько четырехзначных чисел, делящихся на 5, можно составить из цифр 0, 1, 3, 5, 7, если каждое число не должно содержать одинаковых цифр?
Ответ: 42.
16. Сколько различных светящихся колец можно сделать, расположив по окружности 10 разноцветных лампочек (кольца считаются одинаковыми при одинаковом порядке следования цветов)?
Ответ: 9!.
17. На книжной полке помещается 30 томов. Сколькими способами их можно расставить, чтобы при этом первый и второй тома не стояли рядом?
Ответ: 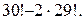
18. Четыре стрелка должны поразить восемь мишеней (каждый по две). Сколькими способами они могут распределить мишени между собой?
Ответ: 2 520.
19. Из группы в 12 человек ежедневно в течение 6 дней выбирают двух дежурных. Определить количество различных списков дежурных, если каждый человек дежурит один раз.
Ответ: 12!/(2!)  .
.
20. Сколько четырехзначных чисел, составленных из цифр 0, 1, 2, 3, 4, 5, содержат цифру 3 (цифры в числах не повторяются )?
Ответ: 204.
21. Десять групп занимаются в десяти расположенных подряд аудиториях. Сколько существует вариантов расписания, при которых группы №1 и №2 находились бы в соседних аудиториях?
Ответ: 2×9!.
22. В турнире участвуют 16 шахматистов. Определить количество различных расписаний первого тура (расписания считаются различными, если отличаются участниками хотя бы одной партии; цвет фигур и номер доски не учитываются).
Ответ : 2 027 025.
23. Шесть ящиков различных материалов доставляются на пять этажей стройки. Сколькими способами можно распределить материалы по этажам? В скольких вариантах на пятый этаж доставлен какой-либо один материал?
Ответ: 56; 6×45.
24. Два почтальона должны разнести 10 писем по 10 адресам. Сколькими способами они могут распределить работу?
Ответ: 210.
25. Поезд метро делает 16 остановок, на которых выходят все пассажиры. Сколькими способами могут распределиться между этими остановками 100 пассажиров, вошедших в поезд на конечной остановке?
Ответ: 16100.
26. Сколько трехзначных чисел, делящихся на 3, можно составить из цифр 0, 1, 2, 3, 4, 5, если каждое число не должно содержать одинаковых цифр?
Ответ: 40.
27. Собрание из 80 человек избирает председателя, секретаря и трех членов ревизионной комиссии. Сколькими способами это можно сделать?
Ответ: 80!(3! ×75!).
28. Из 10 теннисисток и 6 теннисистов составляют 4 смешанные пары. Сколькими способами это можно сделать?
Ответ: 10!/48.
29. Три автомашины №1,2,3 должны доставить товар в шесть магазинов. Сколькими способами можно использовать машины, если грузоподъемность каждой из них позволяет взять товар сразу для всех магазинов и если две машины в один и тот же магазин не направляются? Сколько вариантов маршрута возможно, если решено использовать только машину №1?
Ответ: 36×6!.
30. Четверо юношей и две девушки выбирают спортивную секцию. В секцию хоккея и бокса принимают только юношей, в секцию художественной гимнастики – только девушек, а в лыжную и конькобежную секции – и юношей, и девушек. Сколькими способами могут распределиться между секциями эти шесть человек?
Ответ: 2304.
31. Из лаборатории, в которой работает 20 человек, 5 сотрудников должны уехать в командировку. Сколько может быть различных составов этой группы, если начальник лаборатории, его заместитель и главный инженер одновременно уезжать не должны?
Ответ: 15 368.
32. В фортепьянном кружке занимаются 10 человек, в кружке художественного слова –15, в вокальном кружке – 12, в фотокружке – 20 человек. Сколькими способами можно составить бригаду из четырех чтецов, трех пианистов, пяти певцов и одного фотографа?
Ответ: 15!10/7!
33. Двадцать восемь костей домино распределены между четырьмя игроками. Сколько возможно различных распределений?
Ответ: 
34. Из группы в 15 человек должны быть выделены бригадир и 4 члена бригады. Сколькими способами это можно сделать?
Ответ: 15 015.
35. Пять учеников следует распределить по трем параллельным классам. Сколькими способами это можно сделать?
Ответ: 35.
36. Лифт останавливается на 10 этажах. Сколькими способами могут распределиться между этими остановками 8 пассажиров, находящихся в лифте?
Ответ: 108.
37. Восемь авторов должны написать книгу из шестнадцати глав. Сколькими способами возможно распределение материала между авторами, если два человека напишут по три главы, четыре – по две, два – по одной главе книги?
Ответ: 16!/(26×32).
38. В шахматном турнире участвуют 8 шахматистов третьего разряда, 6 – второго и 2 перворазрядника. Определить количество таких составов первого тура, чтобы шахматисты одной категории встречались между собой (цвет фигур не учитывается).
Ответ: 420.
39. Из цифр 1, 2, 3, 4, 5, 6, 7, 8, 9 составляются всевозможные пятизначные числа: не содержащие одинаковых цифр. Определить количество чисел, в которых есть цифры 2, 4 и 5 одновременно.
Ответ: 1800.
40. Семь яблок и два апельсина надо положить в два пакета так, чтобы в каждом пакете был хотя бы один апельсин и чтобы количество фруктов в них было одинаковым. Сколькими способами это можно сделать?
Ответ: 105.
41. Буквы азбуки Морзе состоят из символов (точек и тире). Сколько букв можно изобразить, если потребовать, чтобы каждая буква содержала не более пяти символов?
Ответ: 62.
42. Номер автомобильного прицепа состоит из двух букв и четырех цифр. Сколько различных номеров можно составить, используя 30 букв и 10 цифр?
Ответ: 9×106.
43. Садовник должен в течение трех дней посадить 10 деревьев. Сколькими способами он может распределить по дням работу, если будет сажать не менее одного дерева в день?
Ответ: 36.
44. Из вазы, где стоят 10 красных и 4 розовых гвоздики, выбирают один красный и два розовых цветка. Сколькими способами это можно сделать?
Ответ: 60.
45. Двенадцати ученикам выданы два варианта контрольной работы. Сколькими способами можно посадить учеников в два ряда, чтобы у сидящих рядом не было одинаковых вариантов, а у сидящих друг за другом был один и тот же вариант?
Ответ: 2(6!)2.
46. Каждый из десяти радистов пункта А старается установить связь с каждым из двадцати радистов пункта Б. Сколько возможно различных вариантов такой связи?
Ответ: 2200.
47. Шесть ящиков различных материалов доставляют на восемь этажей стройки. Сколькими способами можно распределить материалы по этажам? В скольких вариантах на восьмой этаж будет доставлено не более двух материалов?
Ответ: 86; 86–13×75.
48. Сколькими способами можно построить в одну шеренгу игроков двух футбольных команд так, чтобы при этом два футболиста одной команды не стояли рядом?
Ответ: 2(11!)2.
49. На книжной полке книги по математике и по логике – всего 20 книг. Показать, что наибольшее количество вариантов комплекта, содержащего 5 книг по математике и 5 книг по логике, возможно в том случае, когда число книг на полке по каждому предмету равно 10.
Ответ: C510–x × C510+x  (C510)2 .
(C510)2 .
50. Лифт, в котором находятся 9 пассажиров, может останавливаться на десяти этажах. Пассажиры группами выходят по два, три и четыре человека. Сколькими способами это может произойти?
Ответ: 10!/4.
51. «Ранним утром на рыбалку улыбающийся Игорь мчался босиком». Сколько различных осмысленных предложений можно составить, используя часть слов этого предложения, но не изменяя порядка их следования?
Ответ: 23.
52. В шахматной встрече двух команд по 8 человек участники партий и цвет фигур каждого участника определяются жеребьевкой. Каково число различных исходов жеребьевки?
Дата добавления: 2021-07-19; просмотров: 202; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
