Отрицание кварторных предикатов.
Два предиката будем считать равносильными, если их значения истинности совпадают при всех значениях входящих в них свободных переменных. При этом имеется в виду, что свободные переменные в одном предикате не являются связанными в другом.
Справедливы следующие равносильности, относящиеся к отрицаниям кванторных предикатов:
 .
.
Действительно, в первой из них левая часть читается: неверно, что для каждого x предикат P(x) истинен; правая - существует x, для которого P(x) пожен. Ясно, что эти два утверждения имеют один и тот же смысл. Аналогичным рассуждением убеждаемся в спроведливости второй равносильности.
Таким образом, знак отрицания можно ввести пол знак квантора, заменив квантор на двойственный.
Очевидно, что все равносильности, имеющие место в алгебре высказываний, пере-„носится и на алгебру предикатов.
Пример.


Формулы, в которых из операций алгебры высказываний имеются только операции  а знаки отрицания относятся только к элементарным предикатам, называются приведенными формулами.
а знаки отрицания относятся только к элементарным предикатам, называются приведенными формулами.
Пример 1. Какие из следующих выражений являются формулами логики предикатов? В каждой формуле выделите свободные и связанные переменные.
1) 
2) 
3) P(x)& 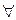 x Q(x);
x Q(x);
4) 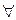 x (P(x) →Q(x)) ↔ (
x (P(x) →Q(x)) ↔ ( 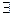 x P(x) →
x P(x) → 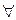 x R(x,y));
x R(x,y));
5) (P(x) ↔Q(x)) v 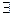 y (
y ( 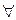 y R(y));
y R(y));
6) 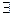 x
x 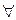 z (P(x,y) →P(y,z)).
z (P(x,y) →P(y,z)).
Решение. Выражения 1), 2), 4), 6) являются формулами, так как записаны в соответствии с определением формулы логики предикатов. Выражения 3) и 5) не являются формулами. В выражении 3) операция конъюнкция применена к формулам Р(х) и 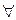 x Q(x); в первой из них переменная х свободна, а во второй связана квантором общности, что противоречит определению формулы. В выражении 5) квантор существования по переменной у навешен на формулу
x Q(x); в первой из них переменная х свободна, а во второй связана квантором общности, что противоречит определению формулы. В выражении 5) квантор существования по переменной у навешен на формулу 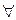 y R(y), в которой переменная у связана квантором общности, что также противоречит определению формулы.
y R(y), в которой переменная у связана квантором общности, что также противоречит определению формулы.
|
|
|
В формуле 1) переменная у свободна, а переменные х и z связаны. В формуле 2) нет предметных переменных. В формуле 4) переменная х связана, а переменная у свободна.
О логическом значении формулы логики предикатов можно говорить лишь тогда, когда задано множество М, на котором определены входящие в эту формулу предикаты. Логическое значение формулы логики предикатов зависит от значения трех видов переменных, входящих в формулу:
а) переменных высказываний;
б) свободных предметных переменных из множества М;
в) предикатных переменных.
При конкретных значениях этих переменных формула принимает конкретное логическое значение.
Пример 2. Дана формула 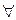 x(P(x)&Q(x) →R(x)), где предикаты Р(х}, Q(x) и R(x) определены на множестве N. Найти ее значение, если
x(P(x)&Q(x) →R(x)), где предикаты Р(х}, Q(x) и R(x) определены на множестве N. Найти ее значение, если
|
|
|
Р(х): «число х делится на 3», Q(х): «число х делится на 4», R{x) : «число х делится на 2»;
Р(х): «число х делится на 3», Q(x): «число х делится на 4», R(x): «число х делится на 5».
Решение. В обоих случаях конъюнкция P(x)&Q(x) есть утверждение, что число х делится на 12. Но тогда при всех х, если число х делится на 12, то оно делится и на 2, и, значит, в случае 1) формула истинна.
Так как из делимости числа х на 12 не при всех х следует делимость числа х на 5, то в случае 2) формула ложна.
Пример 3. Вычислить значение формулы 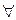 х
х 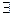 у P(х,у) →
у P(х,у) → 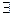 х
х 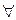 у Р(х,у), если предикат Р(х,у) имеет значение Р0(х,у) - «число x меньше числа у» иопределен на множестве М = N х N.
у Р(х,у), если предикат Р(х,у) имеет значение Р0(х,у) - «число x меньше числа у» иопределен на множестве М = N х N.
Решение. Так как при указанном значении предиката Р(х, у) высказывание 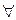 x
x 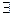 у Р(х,у) означает утверждение, что для любого натурального числа х найдется натуральное число у, большее числа х, то это высказывание истинно. В то же время высказывание
у Р(х,у) означает утверждение, что для любого натурального числа х найдется натуральное число у, большее числа х, то это высказывание истинно. В то же время высказывание 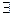 х
х 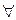 у Р(х,у) означает утверждение, что существует натуральное число х, которое меньше любого натурального числа у, которое ложно. При этом исходная формула, очевидно, ложна.
у Р(х,у) означает утверждение, что существует натуральное число х, которое меньше любого натурального числа у, которое ложно. При этом исходная формула, очевидно, ложна.
Дата добавления: 2021-07-19; просмотров: 102; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
