Свойства объединения и пересечения множеств
Из определений объединения и пересечения множеств вытекают свойства этих операций, представленные в виде равенств, справедливых для любых множеств A, B и С .
A È B = B È A – коммутативность объединения;
A Ç B = B Ç A – коммутативность пересечения;
A È (B ÈС) = (A È B) È С – ассоциативность объединения;
A Ç (B ÇС) = (A Ç B) Ç С – ассоциативность пересечения;
A Ç (B ÈС) = (A Ç B) È (A Ç С) – дистрибутивность пересечения относительно объединения;
A È (B ÇС) = (A È B) Ç (A È С) – дистрибутивность объединения относительно пересечения;
законы поглощения:
A È A = A
A Ç A = A
A È Ø = A
A Ç Ø = Ø
A È U = U
A Ç U = A
Следует заметить, что разность не обладает свойствами коммутативности и ассоциативности, то есть A \ B ≠ B \ A и A \ (B \ С) ≠ (A \ B) \ С. В этом легко убедиться, построив диаграммы Эйлера - Венна.
Симметрическая разность АΔВ = (А\ В) U (В\ А).
Пример 1. Пусть универсальное множество U- множество всех сотрудников некоторой фирмы; А - множество всех сотрудников данной организации старше 35 лет; В - множество сотрудников, имеющих стаж работы более 10 лет; С -множество менеджеров фирмы. Каков содержательный смысл (характеристическое свойство) каждого из следующих множеств:
а) В; б) А ∩ В ∩ С; в)А U (В ∩ С); т)В\С; д)С\В?
► а) В - множество сотрудников организации, стаж работы которых не превышает 10 лет.
|
|
|
б) А ∩ В ∩ С- множество менеджеров фирмы не старше 35 лет, имеющих стаж работы более 10 лет.
в) А U (В ∩ С) - множество всех сотрудников фирмы старше 35 лет, а также сотрудников, не являющихся менеджерами, стаж работы которых более 10 лет.
г) В \ С - множество сотрудников организации со стажем работы более 10 лет, не работающих менеджерами.
д) С \ В - множество менеджеров со стажем работы не более 10 лет.
Декартово (прямое) произведение множеств А и В: АхВ=С.
3. Декартовым произведением АхВ является множество С всех упорядоченных пар <аi,bi|>,где aiєA, bjєB, т.е.
C=AxB={<aj,bj> : aiєA и biєВ}.
Иллюстрацией Декартова произведения множеств А={а1|,а2}и В={b1b2,bз} является рис. 1.1.3.
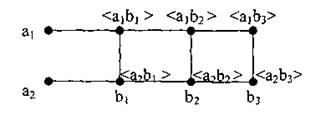
Рис. 1.1.3
В общем случае декартовым произведением множеств А1 А2,... Ап называется множество
A1xA2x ... xAп={<a1, а2, ... ап> : а1єА1 а2єА2... апєАп)
Пример 3. Осуществить операции над множествами A={a, b, c, d} и B = {c, d, e, f, g, h).
► А U B= {a, b, с, d, e, f, g, h};A ∩ B = {с, d).
Универсальное множество U не определено, поэтому, строго говоря, операции дополнения над множествами А и В не могут быть выполнены. Дополним условие. Пусть U = {a, b, c, d, f, g, h}, тогда A = U\A = {e, f, g, h}, B = a, b}. A\B={a, b}; B\A = {e, f, g, h}.
Упражнение 1.
Пусть заданы три числовых множества А={2,3,4,10}, В={ 1,2,10,12}, С={1,9,10}.Требуется указать элементы множеств
|
|
|
a) A∩BUB∩C=D, б) (АUС) \ (В∩А)=Е.
Множество «D» есть объединение двух множеств А∩В и В∩С, что следует из порядка выполнения действий.
А∩В={2,10},В∩С={1,10} и D={ 1,2,10}.
Множество «Е» есть разность между объединением АUС и пересечением В∩А.
AUC=( 1,2,3,4,10,12}, В∩А={2,10) и Е={1,3,4,12}.
Упражнение 2.Пусть U= {а, b, с, d},X= {а, с}, Y= {a, b, d},Z= {b, с}. Найти множества: _
a)XÇY; б)(XÇZ)ÈY; b)XÈ(YÇZ);
г)(XÈY)Ç(XÈZ); д)ХÈY; е)XÇY;
ж)ХÇY 3)(XÈY)ÈZ; и)XÈ(YÈZ);
к)X\Z; л)(X\Z)È(Y\Z).
Упражнение 3. Пусть U={1, 2, 3, 4, 5, 6};A = {1, 2, 3}; B ={1, 3, 5, 6}; С ={4, 5, 6}. Найти множества:
a)А\С б)В\С; в)С\В; г)А\В;
д)AÇB; е)ВÇА; ж)АÇС; з)(СÈА)\(СÇА).
6.3 Векторы, прямые произведения, проекции
векторов
Основные понятия векторных представлений:
Вектор v - упорядоченный набор элементов
v = (a1, a2, ..., an),
где а1, а2,..., an - компоненты (координаты) вектора. Число n компонент называется длиной (размерностью) вектора.
|
|
|
Два вектора v1 = (a1, a2, ..., an) и v2= (b1, b2, ..., bn) равны, если они имеют одинаковую длину и соответствующие координаты их равны, т.е.
(a1, a2, ..., an) = (b1, b2, ..., bn), если: 1) n = m; 2) а1 = b1, a2 = b2,..., an = bn.
Проекцией вектора v на i-ю ось называется его i-я компонента:
прiv = ai.
Проекцией вектора v на i-ю ось номерами i1, i2, ..., ik называется вектор длины k:
Пример 2. Пусть V- {(a, b, d), (с, b, d), (d, b, b)}. Чему равны проекции V на первую ось, на вторую, а также на вторую и третью? Чему равны проекции Fra эти оси, если V - упорядоченное (указанным выше образом) множество векторов V?
► Проекции множества векторов V:
np1V= {а, с, d); np2V = {b}; np23V = {(b, d), (b, b)}.
Проекции упорядоченного множества векторов
V - ((а, b, d), (c,b,d),(d,b,b)):
np1V = (а, с, d); np2V = (b, b, b); np3V = ((b, d), (b, d), (b, b)).
Пример 3. Пусть V = {(a, b), (b, с, d), (с, а, d)}. Чему равна проекция np1V
► Проекция np1V не может быть определена, так как задано множество V векторов разной длины.
Пример 4. Пусть X = {0,1}, Y= {а, b}. Найти Х∙Y, Y∙X, Х2, X∙Y∙X.
► X∙Y = {(0, a),(0, b),(l, a),(1, b)}.
Y∙X={(a, 0),(a, l),(b, 0),(b, l)}.
Таким образом, X∙Y=Y∙X.
Х2 = {(0,0), (0,1), (1,0), (1,1)}.
Х∙Y∙Х= {(0, а, 0), (0, а, 1), (0, b, 0), (0, b, 1), (1, а, 0), (1, а, 1), (1, b, 0), (1, b, 1)}.
Упражнения
2. Определить проекции множества векторов V: пр1V, пр2 V, пр3V, если:
|
|
|
а) {(2, X 1,1), (2, 2, 3,1), (1,2, 3,1)};
б) {(1,3, 5), (2, 4, 6), (3,5, 7)}.
З. Пусть Х= {а, с}, Y= {a, d, f}. Найти X•Y, X2, Y•X•Y.
6.4 Домашнее задание.
Пусть А = {1,2}, В = {2,3}, С = {1,3}. Найти: (AÈB) \ (AÇB).
Пусть U= {1,2, 3,4}, А = {1, 3,4}, В = {2, 3}, С ={1,4}. Найти: (В\А)ÈС.
Пусть A1 = A2 = {а, 6, с}, A3 = A4 = {d, е) и V=A1•A2•А3•A4. Найти: пр1V, пр1,3V.
7 Занятие №7
7.1 Контрольная работа по темам: Диаграммы,
решение задач, операции над множествами
Билет №1.
1) Определите, кто из четырех студентов сдал экзамен, если известно:
1. Если первый сдал, то и второй сдал.
2. Если второй сдал, то третий сдал или первый не сдал.
3. Если четвертый не сдал, то первый сдал, а третий не сдал.
4. Если четвертый сдал, то и первый сдал.
2) Постройте диаграммы Эйлера – Венна:
3) Изобразите на координатной плоскости области истинности предикатов.
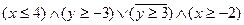
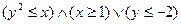
4) Даны множества А{1,2,3,4,5,6}, B{4,5,6,7,8,9}, C{2,4,6}.
Найдите: (АUB)∩C, A\B\C B∆C
5) Дано множество векторов A{(a,s,d), (s,f,h), (d,c,g)} найдите пр1А, пр2А, пр2,3А
Билет №2.
1) Известно следующее: если Петя не видел Колю на улице, то либо Коля ходил в кино, либо Петя сказал правду; если Коля не ходил в кино, то Петя не видел Колю на улице, и Коля сказал правду; если Коля сказал правду, то либо он ходил в кино, либо Петя солгал. Выясните, ходил ли Коля в кино.
2) Постройте диаграммы Эйлера – Венна:
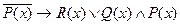
3) Изобразите на координатной плоскости области истинности предикатов.
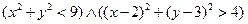
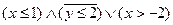
4) Даны множества А{а,б,в,г,д}, B{г,д,у,ё,ж,з}, C{ф,б,у,з}.
Найдите: (А∩B)UC, (A∩B)\C А∆C
5) Дано множество векторов A{(a,s,d,у), (s,f,h,а), (d,c,g,р)} найдите пр4А, пр2А, пр2,4А
Билет №3.
1) Чтыре студентки, имена которых начинаются буквами А, Е, С, Р посещают институт по очереди и ведут общий конспект лекций. Необходимо составить график посещения на ближайшую неделю, учитывая, что:
1. Понедельник - день самостоятельной работы на курсе, и в институт не ходит никто, а в субботу необходимо быть всем.
2. С и Р не смогут пойти на занятия во вторник в связи с большой загруженностью в понедельник.
3. Если С выйдет в среду или Р - в четверг, то Е согласится побывать на занятиях в пятницу.
4. Если А не пойдет в ВУЗ в четверг, то Е позволит себе сходить туда в среду.
5. Если А или Р будут в институте в среду, то С сможет пойти в пятницу.
6. Если Р в пятницу вместо института пойдет на свадьбу подруги, то А придется сходить в институт во вторник, а С - в четверг.
2) Постройте диаграммы Эйлера – Венна:
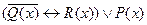
3) Изобразите на координатной плоскости области истинности предикатов.
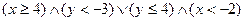
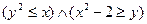
4) Даны множества А{a,,d,f,g,h}, B{g,h,j,k,l,q}, C{f,j,l,t,y}.
Найдите: (А\B)∩C, (A\B)∩C B∆A
5) Дано множество векторов A{(a,s,d,k), (s,f,h), (d,c,g)} найдите пр1А, пр2А, пр2,3А
Билет №4.
1) Четыре друга - Антонов (А), Вехов (В), Сомов (С), Деев (Д) решили провести каникулы в четырех различных городах - Москве, Одессе, Киеве и Ташкенте. Определите, в какой город должен поехать каждый из них, если имеются следующие ограничения:
1. Если А не едет в Москву, то С не едет в Одессу.
2. Если В не едет ни в Москву, ни в Ташкент, то А едет в Москву.
3. Если С не едет в Ташкент, то В едет в Киев.
4. Если Д не едет в Москву, то В не едет в Москву.
5. Если Д не едет в Одессу, то В не едет в Москву.
2) Постройте диаграммы Эйлера – Венна:
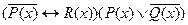
3) Изобразите на координатной плоскости области истинности предикатов.
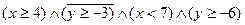
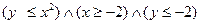
4) Даны множества А{4,5,6,7,8,9}, B{1,3,6,9,12,15}, C{2,5,9,14,15}.
Найдите: (А∆B)∩C, A∩(B\C) A∆C
5) Дано множество векторов A{(a,s,d), (s,f,h), (d,c,g)} найдите пр2А, пр3А, пр1,3А
Билет №5.
1) В школе, перешедшей на самообслуживание, четырем старшеклассникам: Андрееву, Костину, Савельеву и Давыдову поручили убрать 7-ой, 8-ой, 9-ый и 10-ый классы. При проверке оказалось, что 10-ый класс убран плохо. Не ушедшие домой ученики сообщили о следующем:
1. Андреев: «Я убирал 9-ый класс, а Савельев - 7-ой».
2. Костин: «Я убирал 9-ый класс, а Андреев - 8-ой».
3. Савельев: «Я убирал 8-ой класс, а Костин - 10-ый».
Давыдов уже ушел домой. В дальнейшем выяснилось, что каждый ученик в одном из двух высказываний говорил правду, а во втором ложь. Какой класс убирал каждый ученик?
2) Постройте диаграммы Эйлера – Венна:
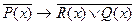
3) Изобразите на координатной плоскости области истинности предикатов.
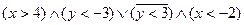
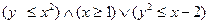
4) Даны множества А{q,w,e,r,t,y}, B{r,t,y,u,i,o}, C{w,t,i,v,d}.
Найдите: (CUB)∩A, C∆B\A C∩A∩B
5) Дано множество векторов A{(a,s,d,t), (s,f,h,b), (d,c,g,a)} найдите пр1А, пр3А, пр2,4А
Билет №6.
1) Пять школьников из пяти различных городов Брянской области прибыли для участия в областной олимпиаде по математике. На вопрос: «Откуда Вы?» каждый дал ответ:
Иванов: «Я приехал из Клинцов, а Дмитриев — из Новозыбкова».
Сидоров: «Я приехал из Клинцов, а Петров - из Труб-чевска».
Петров: «Я приехал из Клинцов, а Дмитриев - из Дятькова».
Дмитриев: «Я приехал из Новозыбкова, а Ефимов -из Жуковки».
Ефимов: «Я приехал из Жуковки, а Иванов живет в Дятькове».
Откуда приехал каждый из школьников, если одно утверждение верно, а другое ложно?
2) Постройте диаграммы Эйлера – Венна:
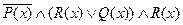
3) Изобразите на координатной плоскости области истинности предикатов.
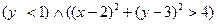
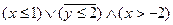
4) Даны множества А{3,4,5,6,7,8,9}, B{1,4,8,12}, C{2,4,5,7,9}.
Найдите: (АUB)∩C, A\C\B B∆A
5) Дано множество векторов A{(a,s,d,t,u), (s,f,h,e), (d,c,g,t,i)} найдите пр1А, пр4А, пр3,4А
8 Занятие №8
8.1 Предикаты
Предикат - повествовательное предложение, содержащее предметные nеременные, определенные на соответствующих множествах; при замене переменных конкретными значениями (элементами) этих множеств предложение обращается в высказывание, Т.е. принимает значение "истинно" или "ложно", Обозначение предиката, содержащего n переменных (n-местного предиката): Р (х 1 , х 2 , … , х n ) при этом предполагается, что х 1 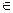 М1, х 2
М1, х 2 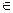 М2, , х n
М2, , х n 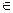 Мп.
Мп.
В качестве примера рассмотрим три высказывания:
А - "Рубль - валюта России" ;
В - "Доллар - валюта России" ;
С - "Доллар - валюта США".
Высказывания А и С - истинны, а В - ложно. Если вместо конкретных наименований валюты в выражениях А, В (и, может быть, аналогичных им) подставить предметную переменную Х и определить ее на множестве наименований денежных единиц Х Е {рубль, доллар, фунт стерлингов, ... , марка}, то получим одноместный предикат Р(х) - "х - валюта России".
Если в выражениях А, В, С (или аналогичных им) вместо конкретных наименований валюты и государства подставить соответственно переменные Х и у, где у Е {Россия, США, Англия, ... , Германия}, получим двухместный предикат Р(х, у) - "х - валюта у". Общим для этих предикатов является то, что, приписав значения входящим в них переменным из соответствующих областей определения, получим высказывания, обладающие свойством "истинно" или "ложно".
Если при отображении P образом набора 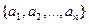 является единица, то записывают.
является единица, то записывают.
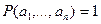
и говорят, что значение предиката P для набора 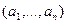 является истинным. Если же образом
является истинным. Если же образом 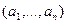 является нуль, то записывают
является нуль, то записывают
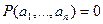
и говорят, что значение предиката P для набора 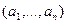 является ложным.
является ложным.
Пусть P(x) - одноместный предикат, заданный на некотором множестве М, Если переменная x обозначает любой элемент из множества М, то P(x) является неопределенным высказыванием.
Операция 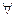 ставит в соответствие неопределенному высказыванию P(x) высказывание
ставит в соответствие неопределенному высказыванию P(x) высказывание 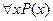 , которое читается так: "для любого x имеет место P(x)" и по определению является истинным тогда и только тогда, когда P(x) истинно для любого элемента
, которое читается так: "для любого x имеет место P(x)" и по определению является истинным тогда и только тогда, когда P(x) истинно для любого элемента 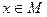 . Переход от неопределенного высказывания P(x) к высказыванию
. Переход от неопределенного высказывания P(x) к высказыванию 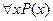 называется операцией навешивания квантора общности по предметному переменному x.
называется операцией навешивания квантора общности по предметному переменному x.
Операция 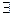 ставит в соответствие неопределенному высказыванию P(x) высказывание
ставит в соответствие неопределенному высказыванию P(x) высказывание 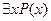 , которое читается так: "существует такое x, что имеет место P(x)" и по определению является испитым тогда и только тогда, когда P(x) истинно хотя бы для одного элемента
, которое читается так: "существует такое x, что имеет место P(x)" и по определению является испитым тогда и только тогда, когда P(x) истинно хотя бы для одного элемента 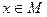 . Переход от неопределенного высказывания P(x) к высказыванию
. Переход от неопределенного высказывания P(x) к высказыванию 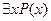 называется операцией навешивания квантора существования по предметному переменному х.
называется операцией навешивания квантора существования по предметному переменному х.
В первом случае мы говорим, что предметная переменная x связана в предикате P(x) квантором всеобщности, во втором случае - квантором существования.
Выражения "x Р(х) и $х Р(х) не зависят от x и при фиксированных Р и М имеют вполне определенные значения, представляя вполне конкретные высказывания относительно всех х предметной области М.
Навешивать кванторы можно и на многоместные предикаты и вообще на любые логические выражения. Выражение, на которое навешивается квантор "х или $х, называется областью действия квантора; все вхождения переменной х в это выражение являются связанными.
Пример 1. Пусть х определен на множестве людей М, а Р(х) — предикат "x - смертен". Дать словесную формулировку предикатной формулы "х Р(х).
Выражение "х Р(х) означает "все люди смертны". Оно не зависит от переменной х, а характеризует всех людей в целом, т.е. выражает суждение относительно всех х множества М.
Пример 2. Пусть Р(х) - предикат "x - четное число", определенный на множестве М. Дать словесную формулировку высказыванию $хР(х), определить его истинность.
Исходный предикат Р(х) - "х - четное число" является переменным высказыванием: при подстановке конкретного числа вместо переменной х он превращается в простое высказывание, являющееся истинным или ложным, например при подстановке числа 5 превращается в высказывание "5 -четное число", являющееся ложным. Высказывание $хР(х) означает "в М существует четное число". Поскольку множество М, на котором задан предикат Р(х), не определено в условии (в таком случае говорят, что задача сформулирована не вполне корректно), доопределим М.
Пусть предикат Р(х) определен на множестве натуральных чисел N, т.е. х Î N, тогда высказывание $хР(х) - истинно. В общем случае высказывание $хР(х) истинно на любом множестве М, содержащем хотя бы одно четное число, и ложно на любом множестве нечетных чисел.
Пример 3. Пусть N(x) - предикат "х - натуральное число". Рассмотреть варианты навешивания кванторов. Проинтерпретировать полученные высказывания и определить их истинность.
> "х N(x) - высказывание "все числа - натуральные" истинно на любом множестве натуральных чисел и ложно, если М содержит хотя бы одно ненатуральное число, например целое отрицательное;
$х N(x) - высказывание "существует натуральное x" истинно на любом множестве М, содержащем хотя бы одно натуральное число, и ложно - в противном случае.
Пример 4. Записать предикатной формулой предложение "Любой человек имеет отца".
Для построения предикатной формулы используем два предиката "x — человек" и "у - отец x" и для удобства восприятия обозначим их соответственно: ЧЕЛОВЕК (x) и ОТЕЦ (у, x). Тогда предложение "Любой человек имеет отца" в предикатной форме имеет вид:
"x (ЧЕЛОВЕК (x) ® $у ОТЕЦ (у, ;x;)).
Заметим, что если предикат ОТЕЦ (у, х) определен на множестве людей, то выражение "любой человек имеет отца" можно записать проще:
"x $у ОТЕЦ (у, х).
Пример 5. Пусть предикат Р(х, у) описывает отношение "x любит у" на множестве людей. Рассмотреть все варианты навешивания кванторов на обе переменные. Дать словесную интерпретацию полученных высказываний.
Обозначим предикат "х любит у" через ЛЮБИТ (x, у). Предложения, соответствующие различным вариантам навешивания кванторов, проиллюстрированы на рис. 5.2, где х и y показаны на разных множествах, что является условностью и предпринято только для объяснения смысла предложений (реальные множества переменных х и у, очевидно, должны совпадать):
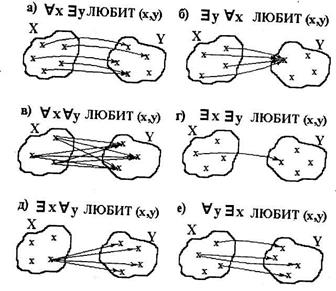
Рис. 5.2
"х $у ЛЮБИТ (х, у)- “для любого человека х существует человек у, которого он любит” (см. рис. 5.2,а) или “всякий человек какого – нибудь любит”;
$у "х ЛЮБИТ (х, у) – “существует такой человек у, что его любят все х” (см. рис. 5.2, б);
"х "у ЛЮБИТ (х, у) - все люди любят всех людей (рис.5.2 в);
$х $у ЛЮБИТ (х, у) – существует человек, который кого-то любит (рис. 5.2,г);
$х "у ЛЮБИТ (х, у) - существует человек, который любит всех людей (рис. 5.2, д);
"y $х ЛЮБИТ (х, у) - "для всякого человека существует человек, который его любит" или "каждого человека кто-то любит" (рис. 5.2, е).
Из приведенного выше можно сделать вывод о том, что перестановка кванторов общности и существования меняет смысл высказывания, т.е. кванторы общности и существования не обладают в общем случае свойством коммутативности.
Пример 6. Пусть Q(x,y) - предикат порядка "х ≤ у'. Рассмотреть различные варианты квантификации его переменных. Определить истинность получаемых выражений для разных случаев интерпретации области определения М предиката, х, у Î М.
> "х(х≤у) - одноместный предикат (переменное высказывание) от у: "для любого х имеет место х ≤у" или "любое число не больше у". Если М - бесконечное множество неотрицательных целых чисел, то этот предикат ложен; на любом конечном множестве натуральных чисел предикат истинен в единственной точке, представляющей наибольшее число в М, например для М= {1,2,3,..., 99} предикат истинен в единственной точке у = 99. При подстановке любого другого .у из М этот предикат обращается в ложное высказывание;
"y (х ≤ у) - одноместный предикат от х: "для любого у имеет место х ≤у" или "любое число из М не меньше х". Если М- множество неотрицательных целых чисел, то этот предикат истинен в единственной точке х = 0и ложен при подстановке вместо х любого другого числа из М;
"х (х ≤ у) - одноместный предикат от .у: "существует число в М, которое не больше у. Если М-любое непустое множество чисел, то данный предикат превращается в истинное высказывание при подстановке какого-либо у из М. Например,если 5 Î М, то при у = 5 получаем $х (х < 5) - истинное высказывание;
$у (х ≤ у) - одноместный предикат от х: "существует число в М, которое не меньше х". На любом непустом множестве М чисел данный предикат превращается в истинное высказывание при подстановке какого-либо х из М.
Пример 7. Рассмотреть все возможные варианты навешивания кванторов на предикат D(x, у) - "х делится на у", определенный на множестве натуральных чисел (без нуля) N. Дать словесные формулировки полученных высказываний и определить их истинность.
> Операции навешивания кванторов приводят к следующим формулам:
"х D(x, у) — одноместный предикат (переменное высказывание) "всякое натуральное число из N делится на натуральное число у из N"; истинный только для одного значения свободной переменной у = 1;
$х D(x, у) - переменное высказывание "существует натуральное число, которое делится на y', истинное для любого значения свободной переменной у, взятой из множества N;
"у D(х,у) — переменное высказывание "натуральное число х делится на всякое натуральное число y”, ложное для любого значения свободной переменной х, взятой из множества N;
$у D(x, у) - переменное высказывание "существует натуральное число, которое делит натуральное число х", истинное для любого значения свободной переменной х;
"x "y D(x, у); "y "x D(x, у) - высказывания "для любых двух натуральных чисел имеет место делимость одного на другое" ложные;
$х $у D(x, у); $у $х D(x, у) - высказывания "существуют такие два натуральных числа, что первое делится на второе", истинны;
$х "y D(x, у) - высказывание "существует натуральное число, которое делится на любое натуральное", ложное;
"y $х D(х, у) - высказывание "для всякого натурального числа найдется такое натуральное, которое делится на первое", истинное;
"x $у D(х, у) - высказывание "для всякого натурального существует такое натуральное число, на которое оно делится", истинное;
$у "x D(x, у) - высказывание "существует натуральное число, которое является делителем всякого натурального числа", истинное (таким делителем являемся единица).
Пример 8. Какой смысл имеют предикатные формулы:
a)"y"z$xП(x,y,z);
б) "x "y "z "u (П(х, у, z) & П(х, у, и) ® E(z, u)), где П,Е - предикаты произведения и равенства, определенные на N ? Истинны ли эти формулы? Привести примеры наборов переменных, иллюстрирующие заключение относительно истинности или ложности формул.
Пример 6. Даны предикаты Р( x): х2 + х +1 > 0 и Q( x): х2 - 4х + 3 = 0, определенные на множестве R. Требуется установить, какие из следующих высказываний истинны и какие ложны:
1) 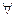 xP( x); 2)
xP( x); 2) 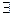 xP( x); 3)
xP( x); 3) 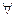 xQ( x); 4)
xQ( x); 4) 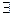 xQ( x).
xQ( x).
Решение. Так как х2 +х + 1 = 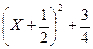 >0 привсех х, то будут истинны высказывания
>0 привсех х, то будут истинны высказывания 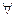 x Р(х) и
x Р(х) и 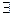 х Р(х).
х Р(х).
Так как уравнение х2 - 4х + 3 = 0 имеет только два действительных корня хг=3 и х2=1. то предикат <?(х) принимает значение 1 только при х=3 и х=1 и О в остальных случаях. Но тогда высказывание 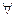 x Q( x) ложно, а высказывание
x Q( x) ложно, а высказывание 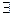 х Q( x) истинно.
х Q( x) истинно.
Пример 7. Пусть предикат Q{ x, y): «х 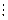 у» определен на множестве N×N. Показать, что высказывания
у» определен на множестве N×N. Показать, что высказывания 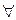 y
y 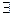 xQ( x, y) и
xQ( x, y) и 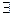 x
x 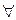 yQ( x, y) имеют различные логические значения.
yQ( x, y) имеют различные логические значения.
Решение. Так как высказывание 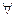 x
x 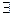 x Q( x,у) означает, что для всякого натурального числа у существует натуральное число х такое, что у является делителем х, то это высказывание истинно.
x Q( x,у) означает, что для всякого натурального числа у существует натуральное число х такое, что у является делителем х, то это высказывание истинно.
Высказывание 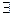 хУу Q( x, y) означает, что есть натуральное число х, которое делится на любое натуральное число у. Это высказывание, очевидно, ложно.
хУу Q( x, y) означает, что есть натуральное число х, которое делится на любое натуральное число у. Это высказывание, очевидно, ложно.
3.7. На множестве М = {1,2,3,...,20} заданы предикаты:
А(х): «х не делится на 5»;
В(х): «x - четное число»;
С(x): «x - число простое»;
D(x): «x кратно 3».
Найдите множества истинности следующих предикатов:
1) А(х)&В(х); 2) С(х)&В(х);
3) C( x)& D( x); 4) B( x)& D( x);
5) 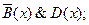 6)
6) 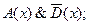
7) 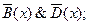 8) A( x)& B( x)& D( x);
8) A( x)& B( x)& D( x);
9) 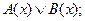 10)
10) 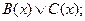
15) 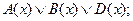 16)
16) 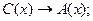
17) 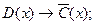 18)
18) 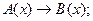
19) 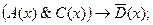 20)
20) 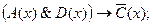
8.2 Понятие формулы логики предикатов. Равносильные формулы логики предикатов
В логике предикатов используется следующая символика:
Символы р, q, r, ... - переменные высказывания, принимающие два значения: 1 - истина, 0 - ложь.
Предметные переменные - *, у, г, ..., которые пробегают значения из некоторого множества М: x0, у0, z0 , ... - предметные константы, то есть значения предметных переменных;
Р(·), F(·) - одноместные предикатные переменные; Q(·,·,...,·), R(·,·,...,·) - n-местные предикатные переменные. Р0(·), Q0(·,·,…,·) - символы постоянных предикатов.
Символы логических операций: &, v , 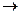 ,-.
,-.
Символы кванторных операций: 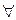 x,
x, 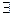 x.
x.
6. Вспомогательные символы: скобки, запятые.
Определение 1. (формулы логики предикатов).
Каждое высказывание как переменное, так и постоянное, является формулой.
Если f(·,·,…,·) - n-местная предикатная переменная или постоянный предикат, а x1, x2, …, xn - предметные переменные или предметные постоянные, не обязательно все различные, то F(x1,x2,...,xn) есть формула. В
этой формуле предметные переменные являются свободными. Формулы вида 1 и 2 называются элементарными.
Если А и В - формулы, причем такие, что одна и таже предметная переменная не является в одной из них связанной, а в другой свободной, то AvB, А&В, А → В есть формулы. В этих формулах те переменные, которые в исходных формулах были свободными, являются свободными, а те, которые были связанными, являются связанными.
Если А - формула, то 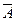 - формула, и характер предметных переменных при переходе от формулы А к формуле
- формула, и характер предметных переменных при переходе от формулы А к формуле 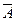 не меняется.
не меняется.
 Если А(х) - формула, в которую предметная переменная х входит свободно, то слова
Если А(х) - формула, в которую предметная переменная х входит свободно, то слова 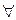 x А(х) и
x А(х) и 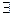 x А(х)являются формулами, причем предметная переменная в них входит связанно.
x А(х)являются формулами, причем предметная переменная в них входит связанно.
Никакая другая строка символов формулой не является.
Переменная, на которую навешен квантор, называется связанной, несвязанная квантором переменная называется свободной.
Дата добавления: 2021-07-19; просмотров: 769; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
