III. Равносильности, выражающие основные законы алгебры логики.
1. 
.
2. 
.
3. 
.
4. 
.
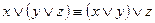5. 
.
6. 
.
Используя равносильности групп I, II, III, можно часть формулы алгебры логики или всю формулу заменить равносильной ей формулой.
Такие преобразования формул применяются для доказательства равносильностей, для приведения формул к заданному виду, для упрощения формул.
Пример 1. Доказать равносильность 
.
Решение. Для доказательства равносильности подвергнём её левую часть равносильными преобразованиями:
.
Пример 2. Упростить формулу 
.
Решение. Подвергнём формулуA равносильным преобразованиям:
Пример 3. Доказать, что формула 
тождественно истинная.
Решение. Подвергнём формулу A равносильным преобразованиям
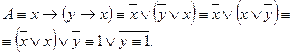
Упражнение 1. Доказать равносильность:
1) 
;
2) 
;
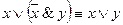3) 
;
4) 
;
5) 
;
Упражнение 2. Упростить формулу:
1) 
;
2) 
;
3) 
;
4) 
.
5) 
;
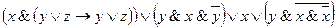6) 
;
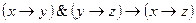Упражнение 3. Доказать тождественную истинность или тождественную ложность формул:
;
;
;
;
;
;
;
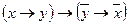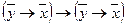Упражнение 4. Найдите x, если 
.
Домашнее задание:
1. Доказать тождественную истинность или тождественную ложность формул:
;
;
2. Упростить:
а) 
;
б) 
;
3 Занятие №3
3.1 Функции алгебры логики. Совершенные нормальные формы
Определение 2. Элементарной конъюнкциейnпеременных называется конъюнкция переменных или их отрицаний.
Определение 3. Дизъюнктивной нормальной формой (ДНФ) формулы A называется равносильная ей формула, представляющая собой дизъюнкцию элементарных конъюнкции.
|
|
|
Определение 4. Совершенной дизъюнктивной нормальной формой (СДНФ) формулы A называется ДНФ A, обладающая свойствами (С).
СДНФ A можно получить двумя способами: а) с помощью таблицы истинности; б) с помощью равносильных преобразований.
Определение 5. Элементарной дизъюнкцией n переменных называется дизъюнкция переменных или их отрицаний.
Определение 6. Конъюнкция нормальной формой (КНФ) формулы А называется равносильная ей формула, представляющая собой конъюнкцию элементарных дизъюнкций.
Определение 7. Совершенной конъюнктивной нормальной формой формулы А (СКНФ А), называется КНФ А, удовлетворяющая четырем свойствам:
1) все элементарные дизъюнкции, входящие в КНФ А, содержат все переменные;
2) все элементарные дизъюнкции, входящие в КНФ А, различны;
3) каждая элементарная дизъюнкция, входящая в КНФ А, содержит переменную один раз;
4) ни одна элементарная дизъюнкция, входящая в КНФ А, не содержит переменную и её отрицание.
СКНФ А можно получить двумя способами: а) с помощью таблицы истинности (используя закон двойственности 
, получаем с помощью таблицы истинности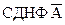 
, и, взяв отрицание 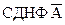, получаем СКНФ А); б) с помощью равносильных преобразований.
Пример 1. Найти формулу, определяющую функцию Ф(x,y,z), по заданной таблице истинности:
|
|
|
| x | y | z | Ф(x,y,z) |
| 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 1 |
Решение. Используя правило получения формулы алгебры логики из таблицы истинности для функции Ф(x,y,z), получим:
.
Упростив эту формулу, получим:
Таким образом, искомой формулой, определяющей функцию Ф(x,y,z), можно считать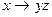 
, или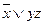 
, или какую-нибудь другого из равносильных формул.
Пример 2. Следующую формулу привести к СДНФ, предварительно приведя её равносильными преобразованиями к ДНФ: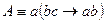 
.
Решение.
Ответ: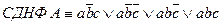 
.
Пример 3. Для формулы из примера 2 найти СДНФ путём составления таблицы истинности.
Решение. Составим таблицу истинности для формулы .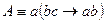
| a | b | C | c | b | 
| A |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 |
Тогда 
.
Пример 4. Для формулы из примера 2 найти СКНФ путём равносильных преобразований, предварительно приведя ее к КНФ.
Решение. Из примера 2: 
. Далее
.
Ответ: 
.
Все формулы алгебры логики делятся на три класса: 1) тождественно истинные; 2) тождественно ложные; 3) выполнимые.
|
|
|
Формулу А называют выполнимой, если она принимает значение 1 хотя бы на одном наборе значений входящих в неё переменных и не является тождественно истиной.
Теорема. Для того, чтобы формула алгебры логики была тождественно истинна (ложна), необходимо и достаточно любая элементарная дизъюнкция (конъюнкция), входящая в КНФ А (ДНФ А), содержала переменную и её отрицание.
Пример 6. Будет ли формула 
тождественно истинной, тождественно ложной или выполнимой?
Решение. Приведём пример к какой-либо нормальной форме:
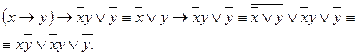
Получение ДНФ не является тождественно ложной, так как каждая элементарная конъюнкция не содержит переменную и её отрицание. Следовательно, исходная формула тождественно истинна или выполнима. Преобразуем данную формулу к КНФ.
Это произведение не является тождественно истинным, так как элементарная сумма 
не тождественно истинна, следовательно, она выполнима.
Упражнение №1. По таблице истинности найдите формулы, определяющие функции 
, 
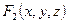, и придайте им более простой вид:
| x | y | z |
|
| |||
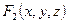
| 1 | 1 | 1 | 0 | 1 | |||
| 1 | 1 | 0 | 1 | 1 | |||
| 1 | 0 | 1 | 1 | 0 | |||
| 1 | 0 | 0 | 1 | 0 | |||
| 0 | 1 | 1 | 0 | 0 | |||
| 0
| 1 | 0 | 0 | 1 | |||
| 0 | 0 | 1 | 1 | 0 | |||
| 0 | 0 | 0 | 0 | 0 | |||
Упражнение №2. Для следующих формул найти СДНФ и СКНФ, каждую двумя способами (путём равносильности преобразований и используя таблицы истинности):
;
;
;
;
;
;
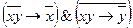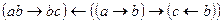Упражнение №3. Используя критерий тождественной истинности и тождественной ложности формулы, установить будет ли данная формула тождественно истинной, тождественно ложной или выполнимой:
1) 
;
2) 
;
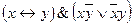3) 
;
4) 
;
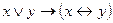5) 
;
6) 
.
3.2 Приложения алгебры логики
I. Приложение алгебры высказываний к релейно-контактным схемам (РКС)
Релейно-контактные схемы (их часто называют переключательными схемами) широко используются в технике автоматического управления.
Под переключательной схемой понимают схематическое изображение некоторого устройства, состоящее из следующих элементов:
1) переключателей, которыми могут быть механические устройства, электромагнитные реле, полупроводники и т.д.;
2) соединяющие их проводники;
3) входы в схему и выходы из нее (клеммы, на которые подается электрическое напряжение). Они называются полюсами.
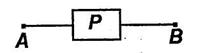
Формулам, включающим основные логические операции, также могут быть поставлены в соответствие переключательные схемы.
Так, конъюнкции двух высказываний p&q ставится в соответствие схема:
а дизъюнкции схема:
Пример 1. Составить РКС для формулы 
Решение. Упростим данную формулу с помощью равносильных преобразований:
Тогда РКС для данной формулы имеет вид*:
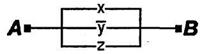
Пример 2. Упростить РКС:
Решение. Составим по данной РКС формулу (функцию проводимости) и упростим ее:
(к последним двум слагаемым применили закон поглощения).
Тогда упрощенная схема выглядит так:
Упражнение №4. Составить РКС для формулы:
1) 
;
2) 
;
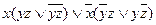3) 
;
7) 
;
8) 
;
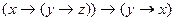Упражнение №5. Упростить РКС:
1.50. Проверить равносильность схем:
1)
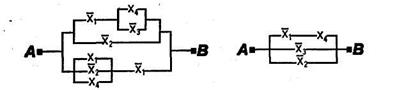
2)
3)
3.3 Домашняя работа
1. По таблице истинности найдите формулы, определяющие функции 
, 
, и придайте им более простой вид:
| x | y | z |
|
|
| 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 0 | 0 | 0 | 0 |
1. Для следующих формул найти СДНФ и СКНФ путем равносильных преобразований.
;
;
2. Проверить равносильность схем:
4 Занятие №4
4.1 Контрольная работа по темам: Равносильные преобразования. СКНФ, СДНФ, РКС
Контроль\КР1_АИС.doc
5 Занятие №5
5.1Решение логических задач с помощью алгебры логики
Задача №1.
Трое друзей спорили о результатах гонок «Формула – 1»
– Вот увидишь, Шумахер не придет первым, – сказал Джон. – Первым будет Хилл.
– Да нет же, победителем будет, Шумахер! – воскликнул Ник. – А об Алези и говорить нечего, ему не быть первым.
Питер сказал:
– Хиллу не видать первого места, а вот Алези пилотирует самую мощную машину.
По завершении гонок оказалось, что каждое из двух предположений двоих друзей подтвердилось, а оба предположения третьего из друзей оказались неверными. Кто выиграл гонки?
Решение:
Пусть Шумахер обозначается Ш; Алези – А, Хилл – Х. Запишем фразы:
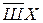
Теперь исходя из предположения, что два друга правы а третий нет запишем сочетания:
Ответ: Шумахер.
Задача №2.
В симфонический оркестр наняли на работу трех музыкантов – Брауна, Смита и Вессона, умеющих играть на скрипке, флейте, альте, кларнете, гобое и трубе. Известно, что:
Смит самый высокий;
играющий на скрипке меньше ростом играющего на флейте;
играющие на скрипке и флейте и Браун не любят пиццу;
когда между альтистом и трубачом возникает ссора их мирит Смит;
Браун не умеет играть ни на трубе, ни на гобое.
На каких инструментах играет каждый музыкант, если известно, что каждый владеет двумя инструментами.
Решение:
Задача решается методом построения таблицы.
| Скрипка | Флейта | Альт | Кларнет | Гобой | Труба | |
| Браун | 0 | 0 | 1 | 1 | 0 | 0 |
| Смит | 0 | 1 | 0 | 0 | 1 | 0 |
| Вессон | 1 | 0 | 0 | 0 | 0 | 1 |
Заполнение таблицы:
Из утверждений №1 и 2 видно, что Смит не играет на скрипке ставим 0.
Из №3 видно, что Браун не играет на скрипке и флейте ставим 0.
Из №4 видно, что Смит не играет на Альте и Трубе.
Из №5 видно, что Браун не играет на Трубе и Гобое.
Так как каждый играет на 2 инструментах, то Браун играет на Альте и Кларнете.
Следовательно Смит и Вессон на них не играют, ставим 0.
Тогда Смит играет на Флейте и Гобое
А Вессон на Скрипке и Трубе.
Задача №3.
Виновник ночного ДТП скрылся с места аварии. Первый из опрошенных свидетелей сказал работникам ГИБДД, что это были «Жигули», первая цифра номера 1. Второй свидетель сказал, что машина была марки «Москвич», а номер начинался с 7. Третий свидетель заявил, что машина была иностранная, номер начинался не с 1. При дальнейшем расследовании выяснилось, что каждый из свидетелей указал правильно либо только марку машины, либо только цифру номера.
Какой марки была машина и на какую цифру начинался номер?
Решение:
Запишем высказывания свидетелей:
Ж (жигули)1;
М (москвич)7;
И (иностранная) 
.
Исходя из условия, что каждый свидетель ошибся в одном предположении, имеем формулу:
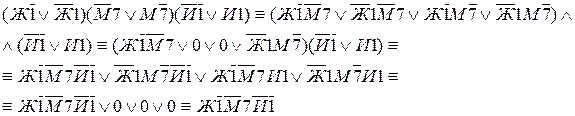Ответ: Жигули номер начинается на 7.
Задача №4.
Пятеро одноклассников – Ирена, Тимур, Камилла, Эльдар и Залим стали победителями олимпиад по физике, математике, информатике, литературе и географии. Известно, что: победитель олимпиады по информатике учит Ирену и Тимура работе на компьютере; Камилла и Эльдар тоже заинтересовались информатикой; Тимур всегда побаивался физики; Камилла, Тимур и победитель олимпиады по литературе занимаются плаванием; Тамур и Камилла поздравляли победителя олимпиады по математике; Ирена сожалеет, что у нее остается мало времени на литературу.
Победителем какой олимпиады стал каждый из этих ребят?
Решение:
Построим таблицу:
| Физика | Математика | Информатика | Литература | География | |
| Ирена | 0 | 1 | 0 | 0 | 0 |
| Тимур | 0 | 0 | 0 | 0 | 1 |
| Камилла | 1 | 0 | 0 | 0 | 0 |
| Эльдар | 0 | 0 | 0 | 1 | 0 |
| Залим | 0 | 0 | 1 | 0 | 0 |
Из №1 получается, что Ирена и Тимур не знают Информатику.
Из №2 получается, что Камилла и Эльдар тоже не знают Информатику.
Тогда получается, что Залим победитель олимпиады по Информатике и на остальных предметах ставятся 0.
Из №3 получается, что Тимур не знает Физику.
Из №4 получается, что Камилла и Тимур не знают Литературы.
Из №5 получается, что Тимур и Камилла не знают Математику.
Тогда получается, что Тимур победитель олимпиады по Географии, соответственно Ирена, Камилла и Эльдар не знают Географию.
Из №6 получается, что Ирена не знает Литературу.
Тогда получается, что Литературу знает Эльдар и не знает остальные предметы.
Отсуда получается, что Ирена знает Математику, а Камилла Физику.
Задача №5.
Семья, состоящая из отца А, матери В и трех дочерей С, D, Е купила телевизор. Условились, что в первый вечер будут смотреть передачи в таком порядке:
1. Когда отец А смотрит передачу, то мать В делает то же.
2. Дочери D и Е, обе или одна из них, смотрят передачу.
3. Из двух членов семьи - мать В и дочь С - смотрят передачу одна и только одна.
4. Дочери С и D или обе смотрят, или обе не смотрят.
5. Если дочь Е смотрит передачу, то отец А и дочь D делают то же.
Кто из членов семьи в этот вечер смотрит передачу?
Решение:
1. 
2. 
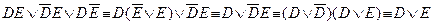
3. 
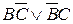
4. 
5. 
Теперь сделаем конъюнкцию 2 и 4, и 1 и 3 выражений:
2 и 4 
1 и 3: 
Далее соберем все вместе:
ОТВЕТ дочери С и D смотрят телевизор.
5.2 Области истинности
3.9. Изобразите на координатной плоскости области истинности предикатов:
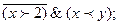
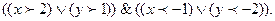
3.8. Изобразите на диаграммах Эйлера-Венна области истинности для следующих предикатов:
1) 
2) 
3) 
4) 
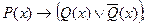
5) 
3.10. Записать предикаты, полученные в результате логических операций над предикатами Р(х), Q(x) и R(x) , области истинности которых (I) заштрихованы на следующих рисунках:
5.3 Домашнее задание
Задание №1. Эйнштейн_задача.doc
2) Изобразите на координатной плоскости области истинности предикатов:
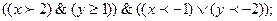
3). Постройте диаграммы Эйлера – Венна для след предикатов:
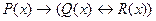
6 Занятие №6
6.1 Множества. Область истинности. Диаграммы Эйлера – Венна
Одно из основных понятий современной математики – понятие множества. Оно является первичным, т. е. не поддается определению через другие, более простые понятия. С понятием множества мы встречаемся довольно часто: буквы русского алфавита образуют множество.
ОПРЕДЕЛЕНИЕ 1: Число объектов множества мы будем называть элементами множества. При этом каждый из объектов данного вида либо принадлежит, либо не принадлежит рассматриваемому множеству.
Так, например, буква ф вне всякого-сомнения принадлежит множеству букв, образующих русский алфавит, в то время как буква f этому множеству не принадлежит.
ОПРЕДЕЛЕНИЕ 2: Множества, включающие только такие объекты, принадлежность или непринадлежность которых к тому или иному множеству не вызывает сомнения, называются четкими множествами.
Четким множествам противопоставлены нечеткие или «лингвистические» множества, включающие такие объекты, которые могут быть отнесены к тому или иному множеству лишь с определенной степенью достоверности.
Понятие нечеткого множества можно проиллюстрировать на примере семантических полей прилагательных младенческий, детский, отроческий, юношеский, молодой, среднего возраста, старый. Чтобы определить границы семантических полей указанных слов и словосочетаний, произведем следующий эксперимент. Предложим большой группе испытуемых – носителей русского языка относить к той или иной возрастной группе мужчин различного возраста. При этом выясняется, что интервал от 10 до 14 лет одними испытуемыми будет квалифицироваться как детский, а другими – как отроческий возраст. Аналогичным образом период от 17 до 23 лет может считаться либо как юношеский, либо как относящийся к молодому возрасту. Таким образом, каждое из рассмотренных семантических полей представляет собой нечеткое подмножество с размытыми краями.
ОПРЕДЕЛЕНИЕ 3: Множества, которые состоят из конечного числа элементов, называются конечными множествами. К числу конечных множеств относится также и пустое множество, т.е. множество, не содержащее ни одного элемента.
Способы задания множества
Произвольные множества будем обозначать прописными, а элементы множества – строчными буквами латинского алфавита, пустое множество – символом Ø.
Дата добавления: 2021-07-19; просмотров: 862; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!