Магнитное квантовое число – m .
Лекция 2
Тема 2 «УЧЕНИЕ О СТРОЕНИИ ВЕЩЕСТВА»
Строение вещества с точки зрения его молекулярной структуры называют макростроением, а строение атомов и молекул – микростроением.
Макростроение.
В зависимости от внешних условий вещества могут находиться в газообразном, жидком, твердом состоянии или в виде плазмы. Каждое из них характеризуется тремя параметрами.
Газообразное состояние. В газах молекулы находятся на значительном удалении друг от друга, и поэтому газовое состояние характеризуется самыми малыми силами межмолекулярного взаимодействия. Газ: 1) не имеет собственной формы;
2)занимает объём, который ему предоставлен;
3) почти не оказывает сопротивления сдвигу.
Жидкое состояние. В жидкости силы взаимодействия больше, чем в газах, но еще недостаточны: 1) для сохранения формы;
но жидкость 2) имеет собственный объём;
и 3) оказывает незначительное сопротивление сдвигу.
Твердое состояние. Различают кристаллическое и аморфное состояния. В твердом веществе частицы находятся на очень близком расстоянии , и силы взаимодействия настолько велики, что твердые вещества: 1) имеют собственный объём;
2) имеют собственную форму;
|
|
|
3) оказывают значительное сопротивление сдвигу.
Сила сопротивления сдвигу измеряется силой внутреннего трения.
Для кристаллического состояния характерны: 1) резкий переход в жидкое состояние (кристалл плавится в одной температурной точке);
2) однородность – тождественность свойств в различных точках;
3) анизотропность – неодинаковость свойств кристалла ( прочность на разрыв, теплопроводность, сжимаемость и др.) в разных направлениях;
4) способность к самоогранению.
Кристаллы симметричные многогранники, характеризующиеся одним или несколькими элементами симметрии: ось, плоскость, центр. 32 сочетания основных элементов симметрии позволяет делить кристаллы на классы. Упорядоченное расположение частиц, образующих кристалл, может быть представлено в виде кристаллической решетки. В зависимости от вида частиц различают: атомную, ионную, молекулярную и металлическую решетки.
|
|
|
Для аморфного состояния характерны: 1) отсутствие упорядоченной структуры;
2) изотропность – одинаковые значения данного свойства при измерении в любом направлении;
3) постепенный переход в жидкое состояние (отсутствие определённой точки плавления).
Плазменное состояние – ионизированный газ, в котором плотности положительных и отрицательных электрических зарядов равны.
Строение атома
2.2.1. Исследования, выполненные в девятнадцатом и начале двадцатого столетий (работы по изучению атомных спектров, открытие Периодического закона Д.И. Менделеевым, открытие катодных и анодных лучей, рентгеновского и радиоактивного излучений и др.), привели к выводу о том, что атом имеет сложное строение: в состав атома входят и положительные и отрицательные частицы. Естественно встал вопрос о модели атома, которая согласуется с экспериментальными данными.
В 1911г. Резерфорд предложил модель атома, в которой положительный заряд сконцентрирован в небольшом объеме в центре атома, а электроны движутся вокруг центра положительного заряда по различным орбитам, как планеты в солнечной системе. По модели Резерфорда, электроны должны двигаться, так как иначе произошло бы сближение противоположно заряженных электронов и ядер. Но в соответствии с требованиями классической электродинамики вращающийся вокруг некоторого центра заряд является источником электромагнитных колебаний, поэтому электрон должен был бы непрерывно излучать энергию и в итоге упасть на ядро, т.е. атом перестал бы существовать. Так как этого не происходит, то следовательно теория Резерфорда была не совсем верна.
|
|
|
В 1913 г. Нильс Бор используя структурную идею модели атома Резерфорда, применил квантовые представления о дискретных энергетических уровнях. Он предположил:
1. движение электрона в атоме ограничено индивидуальной устойчивой орбитой;
2. пока электрон находится на этой орбите, он не излучает энергию;
3. электрон излучает энергию только при переходе с одной орбиты на другую (из одного устойчивого энергетического состояния Е1 в состояние с меньшей энергией Е2) определенными порциями – квантами. Математически это описывается выражением:
hν = E1 – E2, (1)
|
|
|
где h – постоянная Планка, 6,625*10-34 Дж*с;
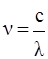- частота колебаний.
В 1916 – 1925 гг. Зоммерфельд разработал теорию многоэлектронных атомов, согласно которой стационарные орбиты могут быть не только круговыми, но и эллиптическими и могут различным образом располагаться в пространстве.
Несмотря на то, что модель Бора количественно описывала линейчатый спектр водородоподобных атомов, она не рассматривала вопрос о том, как это происходит. Бор произвольно совместил уравнения классической механики, электростатики и правила квантования. Кроме того, данную теорию невозможно было применить для количественного объяснения химической связи.
2.2.2. Современная теория строения атомов и молекул основана на законах, описывающих движение микрообъектов – молекул, атомов, ионов, ядер атомов, элементарных частиц и т.д. Эту задачу решает квантовая механика. Законы квантовой механики отличаются от законов классической механики, т.к. они оперируют понятиями вероятности нахождения частицы и ничего не говорят о траектории движения, но сохраняют значения понятий массы и энергии. Основные ее положения основаны на представлениях о двойственной природе (корпускулярно- волновом дуализме) микрообъектов и соотношении неопределенностей.
Корпускулярно-волновой дуализм микрообъектов
Исторически вначале сложились представления о дуализме света. С одной стороны, свет можно представить как электромагнитную волну. Это объясняет явления дифракции, интерференции, преломления света. С другой стороны, рассеяние рентгеновского излучения на электронах (эффект Комптона), фотоэффект, давление света можно объяснить только исходя из представления о свете как о потоке частиц (корпускул).
С одной стороны из закона Эйнштейна:
E = mc2, (2)
где Е – энергия; m – масса; с – скорость света, 3*108 м/с.
С другой стороны, энергия «корпускулы света» - кванта – определяется уравнением Планка:
E = hν = h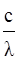 
, (3)
где h – постоянная Планка, ν = 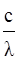- частота колебаний; λ – длина волны.
Приравняв правые части уравнений (1) и (2), получим:
m =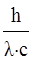 
, (4)
или
λ = 
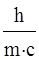, (5)
Взаимосвязь между волновыми характеристиками и массой микрообъекта была выражена в 1924 г. французским физиком Луи де Бройлем уравнением:
λ =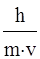 
, (6)
где v – скорость частицы; m – ее масса; λ – длина волны.
Из этого выражения следует, что каждой микрочастице массой ( m ) движущейся со скоростью ( v ) соответствует электромагнитное колебание с длиной волны (λ).
Принцип неопределенности
Другое фундаментальное положение квантовой механики – принцип неопределенности – был сформулирован немецким физиком В.Гейзенбергом в 1927 г.
Математическое выражение соотношения неопределенностей имеет вид:
∆X*∆Px ≥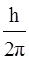 
, (7)
или
∆X*∆vx ≥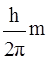 
, (8)
где h – постоянная Планка; ∆Х – неопределенность координаты Х; Рх = mvx – составляющая импульса в направлении координаты Х; ∆Рх и ∆vx – неопределенности составляющих импульса и скорости в направлении координаты Х.
Согласно этому соотношению нельзя одновременно точно определить положение частицы в пространстве и ее импульс. Чем точнее определяется
координата частицы (Х), тем более неопределенным становится ее импульс (Рх), и наоборот.
Аналогичные соотношения справедливы и для координат Y и Z.
2.2.3. Квантовомеханическая модель атома водорода
В 1926 г. австрийский физик Э.Шредингер представил состояние электрона в атоме как трехмерную стоячую волну и описал его дифференциальным уравнением второй степени в частных производных:
- 
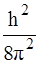m(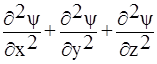 
) + Uѱ = Eѱ , (9)
где U – потенциальная энергия; E – полная энергия; x,y,z – координаты;
ѱ – волновая функция.
Строго определенный смысл имеет квадрат волновой функции: произведение
ѱ2dv равно вероятности нахождения рассматриваемой частицы в элементе объема dv. Величину ѱ2 называют плотностью вероятности, или электронной плотностью ( если речь идет об электроне).
В соответствии с физическим смыслом – волновая функция должна быть конечной, непрерывной и однозначной, а также обращаться в нуль для тех мест пространства, где частица не может находиться.
Таким образом, представление о движении в квантовой механике резко отличается от классического, и правильнее вместо термина «движение электрона» употреблять термин «состояние электрона».
Строгое аналитическое решение уравнения Шредингера возможно только для атома водорода. Для более сложных систем используют приближенный метод.
Квантовые числа
При математическом описании состояния электрона появляются числа, определяющие дискретность его характеристик. Числа называются квантовыми. Их четыре. Три из них обусловлены состоянием электрона в пространстве. Рассмотрим каждое из них.
Главное квантовое число – n .
Из уравнения Шредингера следует, что энергия электрона в атоме водорода дискретна:
Е = - m(e-)4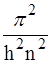 
, (10)
где m – масса электрона, равная 9,11*10-31кг; е- - заряд электрона 1,60*10-19 Кл.
Так как все величины, кромеn , постоянны, то главное квантовое число n в атоме водорода определяет энергию – главную характеристику электрона.
Главное квантовое число принимает целочисленные положительные действительные значения: 1, 2, 3, . . . . . до ∞.
Главное квантовое число характеризует также размер орбитали. Это понятно из общих представлений об электростатическом взаимодействии электрона и ядра: с увеличением n , т.е. с увеличением энергии, должна увеличиваться средняя удаленность электрона от ядра.
Совокупность электронных состояний с определенным значением главного квантового числа называют электронным (или энергетическим) уровнем.
Орбитальное квантовое число – ℓ.
Движение электрона в поле ядра также характеризуется орбитальным моментом импульса количества движения. Его величина определяется орбитальным квантовым числом ℓ.
Орбитальное квантовое число принимает целочисленные положительные значения от 0 до (n – 1).Его принято обозначать не только цифрами, но и латинскими буквами:
Значения ℓ: 0, 1, 2, 3, 4, …….
Обозначение ℓ: s , p , d , f , g , …….
Совокупность электронных состояний с определенным значением n и ℓ называют электронным подуровнем.
Для первого уровня (n = 1) возможно единственное значение орбитального квантового числа: ℓ = 0. Такая орбиталь обозначается 1s, что указывает на значение главного(n = 1) и орбитального (ℓ = 0) квантовых чисел.
Во втором уровне (n =2) орбитальное квантовое число ℓ может принимать два значения: ℓ = 0 (2s) и ℓ = 1 (2p).
В третьем уровне (n = 3) орбитальное квантовое число ℓ может принимать три значения 0, 1, 2. Кроме s - и p - орбиталей появляется d- орбиталь (ℓ =2).
Орбитальное квантовое число ℓ определяет конфигурацию орбитали, которая от значения n не зависит. При ℓ = 0 ( для всех значений главного квантового числа) s – орбитали имеют форму сферическую форму (форму «шара») (рис.1а).
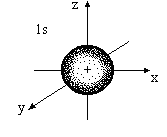
Рис. 1а. Форма s – орбиталей
Форма р – орбиталей менее симметрична, чем s – орбиталей, и похожа на «объемную восьмерку» (форма «гантели») (рис.1б).
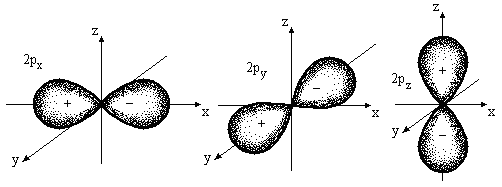
Рис. 1б. Форма р – орбиталей
d – орбитали имеют более сложный вид (рис. 1в).
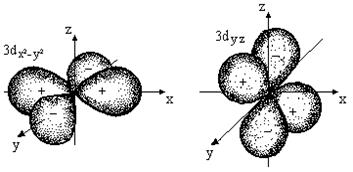
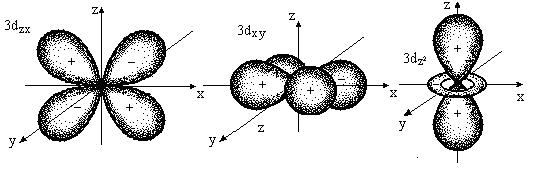
Рис. 1в. Форма d – орбиталей
Магнитное квантовое число – m .
Момент импульса является вектором. Его направление и определяется магнитным квантовым числом m. Таким образом, магнитное квантовое число характеризует ориентацию орбитали в пространстве.
Магнитное квантовое число m принимает значения от (- ℓ), 0, до (+ℓ).
При ℓ = 0 возможно единственное значение m = 0. Действительно для симметричной s – орбитали возможен единственный способ ее ориентации в пространстве (рис. 1а).
Для р – орбитали ℓ = 1. Трем значениям магнитного квантового числа:
m = -1, 0, +1 отвечают три варианта ориентации вектора и соответственно три способа расположения орбитали в пространстве. (рис. 1б)
Для d –орбитали (ℓ =2) в соответствии с m = -2, -1, 0, +1, +2 таких вариантов пять и т.д. (рис. 1в).
Форма и размеры атомных орбиталей (АО) как видно зависят от значений квантовых чисел и следовательно изменяются от одного состояния электрона в атоме к другому. При графическом изображении распределения электронов каждая атомная орбиталь обозначается клеточкой
Дата добавления: 2021-01-21; просмотров: 213; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!