Посещаемость занятий студентами

Академической группы

№ занятия	Число присутствующих
1	17
2	21
3	18
4	14
5	20
6	20
7	16
8	17
9	21
10	22

Источник: гипотетические данные.

Среднее может оказаться обманчивым показателем центральной тенденции, если в объеме выборочной совокупности среди значений интересующей нас переменных появится какая-то экстремальная величина. Например, среднедушевые ежемесячные доходы (приходящиеся на одного члена семьи) в двух гипотетических общинах – скажем, среди жильцов двух подъездов одного дома, каждый из которых насчитывает по 10 квартир, – идентичны, за исключением дохода одного человека (табл.5.9).

Средний доход семьи жителей 1 подъезда – 4230 рублей – более чем вдвое превышает средний доход во 2 подъезде – 2050 рублей. Именно простой расчет среднего дохода в каждом из подъездов создает ошибочное впечатление, что люди в первом подъезде вдвое богаче, чем люди во втором подъезде, тогда как в реальности есть лишь один человек в 1 подъезде, который гораздо богаче любого как из 1, так и из 2 подъезда. В этом случае медиана будет лучшим показателем центральной тенденции, нежели среднее. Медианный подход дал бы для обоих подъездов одинаковый результат: 2100 рублей – довольно близкий к среднему значению по второму подъезду. Если среднее и медиана не сходны по своему значению, можно сделать вывод, что на значение среднего влияют одно или несколько экстремальных значений измеряемой переменной.

Таблица 5.9

Среднедушевые ежемесячные доходы семей

В двух подъездах дома (руб.).

№ кв.	1 подъезд	№ кв.	2 подъезд
1	1000	11	1000
2	3000	12	1000
3	1000	13	1200
4	1800	14	1800
5	25000	15	2000
6	2200	16	2200
7	2500	17	2500
8	2800	18	2800
9	1000	19	3000
10	2000	20	3000
Среднее	4230	Среднее	2050

Источник: гипотетические данные.

Вычисление средней арифметической величины для переменных, значения которых измеряются не однозначно определенными числами, а изменяются вдоль непрерывного ряда значений, имеет свои особенности. Здесь рассчитывается не среднее арифметическое, а средневзвешенное. Так, предположим, что нам требуется вычислить средний возраст респондентов, и распределение по возрасту оказалось таким, как в табл.5.10.

Таблица 5.10

Возраст

	частота	процент
18-24 года	46	10,1
25-29 лет	55	12,0
30-39 лет	97	21,2
40-49 лет	115	25,2
50-59 лет	74	16,2
60-70 лет	70	15,3
Всего	457	100,0

Источник: Аналитический отчет об опросе жителей

г. Нижнего Новгорода, декабрь 1998 г.

Вначале мы должны определить середину каждого интервала. Это делается путем вычисления простого среднего, т.е. сумма крайних значений делится пополам. Затем необходимо умножить это значение на число респондентов соответствующего возраста, сложить полученные произведения и разделить на общий объем выборки. Различные этапы этого процесса отражены в табл.5.10а.

Таблица 5.10а

Возраст

	Частота	Середина интервала	Произведение
18-24 года	46	21	966
25-29 лет	55	27	1485
30-39 лет	97	34,5	3346,5
40-49 лет	115	44,5	5117,5
50-59 лет	74	54,5	4033
60-70 лет	70	65	4550
Всего	457	S	19498

Разделив полученную сумму на 457 (общее число опрошенных), мы получим средний возраст в 42,6 года. Таким образом, формула для средневзвешенного выглядит так же, как и формула (5.1), однако каждое x_i в ней относится к середине интервала:

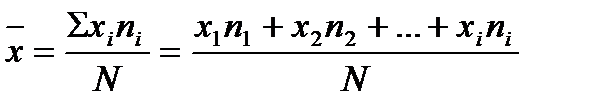(5.2),

где x_i – числовое значение i-й позиции, n_i – число респондентов, наблюдаемых по i-й позиции переменной, а N – общее число наблюдений по всему массиву.

Показатели разброса для данных интервального или пропорционального уровня включают среднее отклонение, дисперсию и среднеквадратичное отклонение. Среднее отклонение (MD) представляет собой меру разброса, основанную на отклонении каждого из значений от среднего. Пример ее вычисления приведен в табл.5.11.

Таблица 5.11

Распределение, отклонение и среднее распределение

Доходов среди жильцов подъезда № 2

№ кв.	Средний доход		\|\|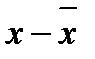
11	1000	-1050	1050
12	1000	-1050	1050
13	1200	-850	850
14	1800	-150	150
15	2000	-50	50
16	2200	50	50
17	2500	450	450
18	2800	750	750
19	3000	950	950
20	3000	950	950
Среднее	2050

Простая алгебраическая сумма отклонений, отраженных в третьей колонке даст нулевой результат:

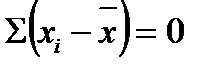Поэтому уравнение для среднего отклонения следует рассчитывать по абсолютным значениям:

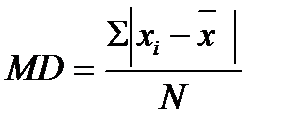(5.3),

где |….| – символ абсолютной величины (модуля).

Если мы берем каждую отметку и вычитаем из нее среднее, мы вычисляем ту величину, на которую каждая из отметок (вторая колонка) отличается от среднего (нижняя ячейка второй колонки). Алгебраическая сумма этих отклонений всегда равна нулю – важное математическое свойство среднего. (Проверьте это сами, сложив числа в третьей колонке.) Поскольку мы интересуемся только величиной отклонения, а не направлением или знаком его, мы находим абсолютные значения отклонения (четвертая колонка). Затем мы берем эту сумму и делим на число отметок, чтобы найти среднее отклонение отметок от среднего; получаем MD = 630. Чем больше среднее отклонение, тем сильнее разброс отметок вокруг среднего.

Хотя среднее отклонение и выявляет разброс, более часто для его измерения используются дисперсия и среднеквадратическое отклонение.

Дисперсия (s²) представляет собой сумму квадратов отклонений от среднего, поделенную на число отметок:

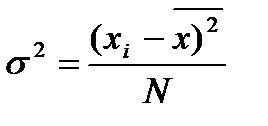(5.4).

Среднеквадратическое отклонение (S) представляет собою корень квадратный из дисперсии:

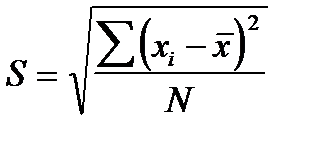(5.5).

Чем больше разброс точек данных вокруг среднего, тем выше значение s²и S. Это означает, что если все данные одинаковы, то s²и S равны нулю.

Таким образом, для вычисления дисперсии и среднеквадратического отклонения надо пройти последовательно семь шагов:

1) вычислить среднее;

2) вычислить разности между средним и каждым из значений;

3) возвести в квадрат разности, вычисленные на этапе 2;

4) умножить квадраты разностей на частоты наблюдений каждого из значений;

5) просуммировать квадраты разностей, вычисленные на этапе 4;

6) разделить сумму квадратов из этапа 5 на N; это равняется дисперсии;

7) извлечь квадратный корень из числа, вычисленного на этапе 6; это равняется среднеквадратическому отклонению.

Мы могли бы привести пример расчета дисперсии и среднеквадратичного отклонения для одной переменной в одном из исследований. В неоднократно упоминавшемся выше опросе, проведенном в конце декабря 1998 года, мы просили нижегородцев оценить некоторые личностные качества недавно избранного мэра, используя для этого так называемый семантический дифференциал^{^[106]}^[15]. Этот метод заключается в следующем: респонденту предлагается выразить свое отношение к интересующему исследователя качеству по степени приближения к тому или иному полюсу биполярной шкалы (в нашем случае девятибалльной). Одно из предложенных для оценки качеств мэра – доступность – было выражено с помощью такой шкалы:

доступный

неприступный

Полученные данные распределились следующим образом:

Таблица 5.12

оценочный балл	частота
нет ответа (0)	62
1	11
2	15
3	44
4	50
5	112
6	56
7	55
8	26
9	26
Всего	457

Отбросив нули, т.е. варианты со значением “нет ответа” (после чего N становится равным уже не 457, а 395), мы подсчитываем, что среднее значение оценки (по формуле средневзвешенного) составляет:

x = 5,31

Обратим внимание: если бы мы не отбросили значений “нет ответа”, т.е. если бы приняли бы эту позицию за нуль как просто математическую величину, то получили бы среднее значение:

x = 4,58,

которое было бы заметно меньше, нежели рассчитанное нами выше. Оно более точное в математическом смысле, но искажает социологический смысл, поскольку ведь те, кто не давали ответа на этот вопрос, вовсе не выставляли оценку “0”, они просто не выставили никакой оценки (или уклонились от нее – по незнанию или иным причинам).

Процедура расчета дисперсии и среднеквадратичного отклонения в соответствии с приведенным выше алгоритмом приведена в табл.5.13:

Таблица 5.13

Образец расчета дисперсии и

Дата добавления: 2020-12-22; просмотров: 132; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 20 21 22 23 242526 27 28 29 Следующая ⇒

Мы поможем в написании ваших работ!