Сумма углов треугольника. Внешний угол треугольника.
Вертикальные и смежные углы. Угол между прямыми.
 При пересечении двух прямых образуется две пары вертикальных углов (Ð1 и Ð3, Ð2 и Ð4 на рисунке 1).
При пересечении двух прямых образуется две пары вертикальных углов (Ð1 и Ð3, Ð2 и Ð4 на рисунке 1).
Теорема о вертикальных углах: Вертикальные углы равны ( 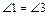 ,
, 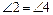 на рисунке 1).
на рисунке 1).
Углом между пересекающимися прямыми называется наименьший из углов, образованных при их пересечении (на рисунке 1 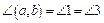 ). Угол между параллельными прямыми считается равным нулю. Таким образом, угол между прямыми меняется в пределах [0°; 90°].
). Угол между параллельными прямыми считается равным нулю. Таким образом, угол между прямыми меняется в пределах [0°; 90°].
 Если из вершины развернутого угла провести луч, образуется два смежных угла (ÐXOZ и ÐZOY на рисунке 2).
Если из вершины развернутого угла провести луч, образуется два смежных угла (ÐXOZ и ÐZOY на рисунке 2).
Теорема о смежных углах: Сумма смежных углов равна 180° (на рисунке 2 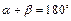 ).
).
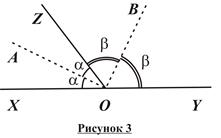 Если провести биссектрисы двух смежных углов (рисунок 3), то по теореме о смежных углах получаем:
Если провести биссектрисы двух смежных углов (рисунок 3), то по теореме о смежных углах получаем: 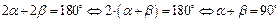 .Таким образом,
.Таким образом,  , то есть биссектрисы смежных углов взаимно перпендикулярны.
, то есть биссектрисы смежных углов взаимно перпендикулярны.
Свойство биссектрис смежных углов: Биссектрисы смежных углов взаимно перпендикулярны.
Углы, образованные при пересечении двух прямых секущей. Признаки и свойства параллельных прямых.
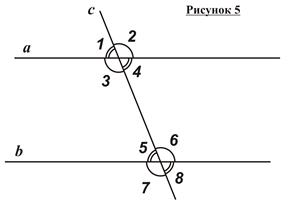
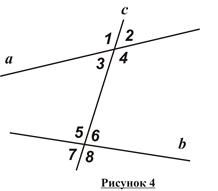 При пересечении двух прямых a и b секущей c (рисунок 4) образуется 8 углов. Среди них различают:
При пересечении двух прямых a и b секущей c (рисунок 4) образуется 8 углов. Среди них различают:
- внутренние односторонние углы (Ð3 и Ð5, Ð4 и Ð6 на рисунке 4);
- внутренние накрест лежащие углы (Ð3 и Ð6, Ð4 и Ð5 на рисунке 4);
- соответственные углы (Ð1 и Ð5, Ð3 и Ð7, Ð2 и Ð6, Ð4 и Ð8 на рисунке 4);
- внешние односторонние углы (Ð1 и Ð7, Ð2 и Ð8 на рисунке 4);
· внешние накрест лежащие углы (Ð1 и Ð8, Ð2 и Ð7 на рисунке 4).
|
|
|
Признаки параллельности прямых позволяют судить о параллельности двух прямых по соотношению между углами, образованными этими прямыми и секущей:
· Если накрест лежащие углы, образованные при пересечении двух прямых секущей, равны, то прямые параллельны (к примеру, если на рисунке 4 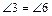 , или
, или  , или
, или  , или
, или  , то aïêb).
, то aïêb).
· Если соответственные углы, образованные при пересечении двух прямых секущей, равны, то прямые параллельны (к примеру, если на рисунке 4 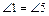 , или
, или  , или
, или 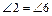 , или
, или  , то aïêb).
, то aïêb).
· Если односторонние углы, образованные при пересечении двух прямых секущей, в сумме дают 180°, то прямые параллельны (к примеру, если на рисунке 4  , или
, или  , или
, или 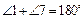 , или
, или  , то aïêb).
, то aïêb).
Из сформулированных признаков параллельности прямых вытекает важное следствие: Две прямые, перпендикулярные третьей прямой, параллельны друг другу.
Если известно, что прямые параллельны (на рисунке 5 aïêb), то углы, образованные при пересечении этих прямых секущей, обладают следующими свойствами:
 Свойства углов, образованных при пересечении параллельных прямых секущей:
Свойства углов, образованных при пересечении параллельных прямых секущей:
· Если прямые параллельны, то накрест лежащие углы, образованные при пересечении их секущей, равны (на рисунке 5 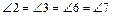 , и
, и 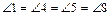 ).
).
|
|
|
· Если прямые параллельны, то соответственные углы, образованные при пересечении их секущей, равны (на рисунке 5 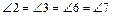 , и
, и 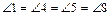 ).
).
· Если прямые параллельны, то односторонние углы, образованные при пересечении их секущей, в сумме составляют 180° (на рисунке 5 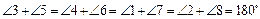 ).
).
Следует различать признаки и свойства углов при параллельных прямых и секущей: если свойства справедливы в случае, когда прямые параллельны (углы при параллельных прямых обладают указанными выше свойствами), то признаки позволяют выяснить, являются ли прямые параллельными. Свойства и признаки называются взаимно обратными теоремами (то, что является причиной в свойстве, в признаке оказывается следствием, и наоборот).
На рисунке 6 изображены биссектрисы углов, образованных при пересечении параллельных прямых AB и CD секущей XY. Пользуясь рисунком, докажем следующее свойство биссектрис углов, образованных при пересечении параллельных прямых секущей: Биссектрисы накрест лежащих или соответственных углов, образованных при пересечении двух параллельных прямых секущей, тоже параллельны. Биссектрисы односторонних углов, образованных при пересечении параллельных прямых секущей, взаимно перпендикулярны.
|
|
|
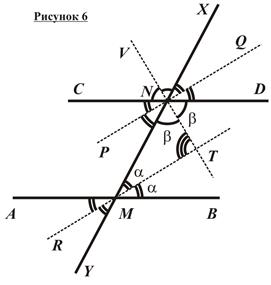 На рисунке 6 ABïêCD. Требуется доказать, во-первых, что PQïêRT (эти прямые содержат биссектрисы накрест лежащих и соответственных углов), а во-вторых – что VT^RT (эти прямые содержат биссектрисы односторонних углов).
На рисунке 6 ABïêCD. Требуется доказать, во-первых, что PQïêRT (эти прямые содержат биссектрисы накрест лежащих и соответственных углов), а во-вторых – что VT^RT (эти прямые содержат биссектрисы односторонних углов).
1. ÐXND и ÐNMB – соответственные при параллельных прямых AB и CD и секущей XY, следовательно, по свойству углов, образованных при пересечении параллельных прямых секущей, ÐXND = ÐNMB. Но тогда 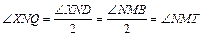 . Поскольку углы XNQ и NMT – соответственные при прямых PQ и RT и секущей XY, то из их равенства следует параллельность прямых PQ и RT по признаку параллельности прямых.
. Поскольку углы XNQ и NMT – соответственные при прямых PQ и RT и секущей XY, то из их равенства следует параллельность прямых PQ и RT по признаку параллельности прямых.
2. ÐMND и ÐNMB – внутренние односторонние при параллельных прямых AB и CD и секущей XY, следовательно, по свойству углов, образованных при пересечении параллельных прямых секущей, 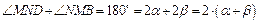 . Тогда
. Тогда 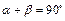 , и по теореме о сумме углов треугольника для DMNT получаем:
, и по теореме о сумме углов треугольника для DMNT получаем:  , то есть VT^RT.
, то есть VT^RT.
Свойство доказано.
Сумма углов треугольника. Внешний угол треугольника.
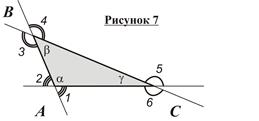 Теорема о сумме углов треугольника: Сумма углов треугольника равна 180° (к примеру, на рисунке 7
Теорема о сумме углов треугольника: Сумма углов треугольника равна 180° (к примеру, на рисунке 7 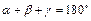 ).
).
Следствие из теоремы о сумме углов треугольника: Сумма двух острых углов прямоугольного треугольника равна 90°.
Внешним углом треугольника называется угол, смежный с его внутренним углом. В треугольнике можно построить по два внешних угла при каждой вершине, то есть у треугольника 6 внешних углов (углы, помеченные цифрами на рисунке 7).
|
|
|
Из теоремы о смежных углах следует, что 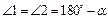 . С другой стороны, по теореме о сумме углов треугольника
. С другой стороны, по теореме о сумме углов треугольника 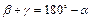 , откуда следует, что
, откуда следует, что  . Полученное утверждение называется теоремой о внешнем угле треугольника: Внешний угол треугольника равен сумме двух несмежных с ним внутренних углов (на рисунке 7
. Полученное утверждение называется теоремой о внешнем угле треугольника: Внешний угол треугольника равен сумме двух несмежных с ним внутренних углов (на рисунке 7  ,
,  ,
, 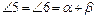 ).
).
Дата добавления: 2020-11-29; просмотров: 157; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
