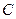Найдем первую и вторую производные

; .

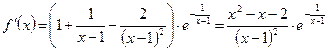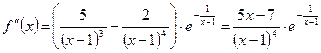Анализ результатов исследования.

Заполняя таблицу, учитываем, что в правой и левой окрестностях точки 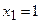поведение графика функции различно.

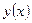
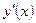
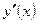
					Выводы
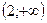
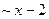
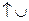					, асимптота ниже графика
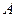
					точка локального минимума

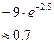
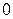
					точка перегиба,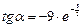

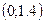
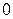
					точка локального минимума с горизонтальной касательной справа, слева – стремление к вертикальной асимптоте


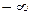
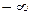
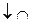
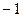
					Точка локального максимума
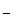
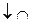					, асимптота выше графика

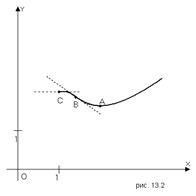
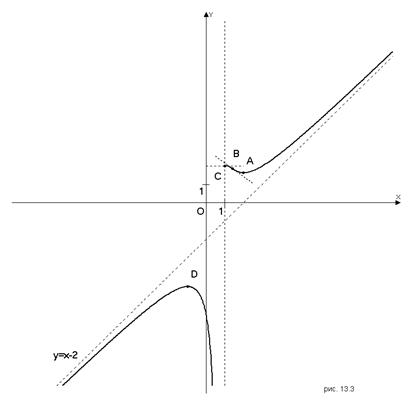
Так как поведение функции в окрестности точки 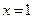трудно изобразить на основном рисунке, сделаем выносной рисунок (рис. 13.2). График функции изображен на рис. 13.3.

Построение кривых[2]

В данном параграфе мы рассматриваем параметрически заданные кривые вида .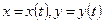

План исследования и построения кривых

1. Исследование функци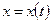й и .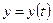

2. Исследование асимптот кривой.

3. Анализ полученных результатов и построение эскиза кривой.

4. Исследование кривой с помощью первой производной, нахождение точек экстремума и точек возврата.

5. Исследование кривой с помощью второй производной, нахождение точек перегиба.

6. Построение кривой.

Основные требования к результатам исследования и построению кривой в целом такие же, как к исследованию и построению графиков функций.

2. Основные понятия и этапы исследования кривой

1. Исследование функци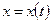й и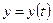

Для построения кривой определяются промежутки изменения параметра 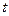, на которых функци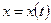и и 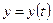монотонны. На промежутке монотонности функции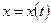 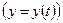кривую можно анализировать как функцию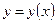 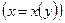, соответственно. Поэтому для построения кривой важно исследовать:

— участки возрастания (убывания) функци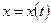й и ;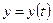

— вертикальные асимптоты;

Наклонные асимптоты графиков функци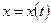й и 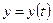исследуются, только если используются их эскизы. Исследование функци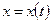й и 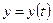с помощью второй производной проводить не нужно.

Результаты исследования функци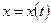й и 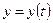могут быть описаны, приведены в виде таблицы или отражены на эскизах графиков этих функций.

2. Использование результатов исследования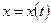

2.1. Вертикальные асимптоты кривой

Прямая 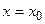является вертикальной асимптотой криво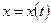й и 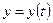, если выполнено хотя бы одно из условий:

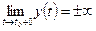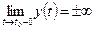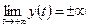, , или 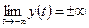, но во всех случаях функция 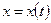монотонно стремится к некоторому конечному значению 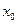при соответствующем изменении параметра 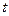. Направление изменения (убывание или возрастание) функции 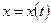определяет, с какой стороны кривая приближается к асимптоте.

2.2. Наклонные (горизонтальные) асимптоты кривой

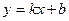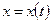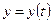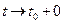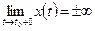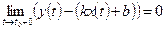Прямая является (невертикальной) асимптотой кривой и , при , если и . Аналогично рассматриваются случаи асимптоты при , , .

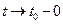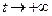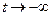Если 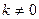, то асимптота называется наклонной. Если 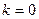, то асимптота 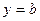называется горизонтальной.

Для нахождения асимптот параметрически заданных кривых основным является метод вычисления пределов. Из определения асимптоты при 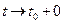следует, что 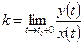, 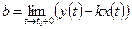. Вычисляя соответствующие пределы, получаем уравнение асимптоты 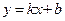. Другие случаи рассматриваются аналогично.

Взаимное расположение асимптоты и кривой можно проанализировать, во-первых, оценивая знак выражения 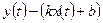, во-вторых, по направлению выпуклости кривой, аналогично функции (см. п.1). Взаимное расположение асимптоты и кривой можно определить, анализируя промежутки изменения функци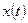й и 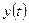при приближении к асимптоте.

3. Анализ результатов и построение эскиза графика функции

Полученные на данном этапе результаты исследования позволяют построить эскиз кривой, указывающий основные моменты поведения и приблизительно предположить взаимное расположение особых точек кривой. Такой анализ необходим для проверки дальнейших результатов исследования кривой с помощью производной.

Построение эскиза и самой кривой начинается с изображения на координатной плоскости вертикальных и наклонных (горизонтальных) асимптот кривой. Если известны точки пересечения кривой с осями, полезно отметить их на координатной плоскости для уточнения ее поведения.

Соотношение участков возрастания и убывания функци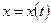й и 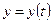используем при построении эскиза кривой и для определения значений параметра 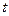, при которых возможно стремление к асимптоте.

4. Участки возрастания и убывания кривой. Точки минимума и максимума функци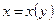й и 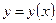, точки возврата кривой

Участки возрастания и убывания кривой исследуются на интервалах параметра 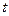, на которых определена функция 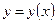по знаку производной 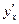аналогично исследованию функций.

Приведем в таблице зависимость монотонности кривой от монотонности функци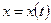й и 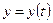на интервале 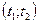и знаков производной .

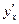	1 случай	2 случай	3 случай	4 случай



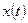
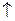
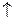
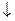
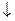
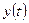
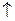
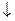
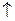
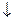
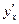
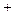
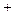
кривая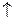

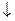
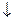
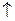
Точка 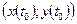называется точкой минимума (максимума) кривой, если в окрестности точки 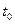определена функция 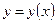и точка 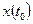является ее точкой минимума (максимума). Исследование точек минимума (максимума) осуществляется аналогично исследованию функций. Производная 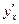или соответствующие односторонние производные, вычисляются по формуле дифференцирования функции, заданной параметрически.

Точка 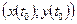называется точкой минимума (максимума) функции 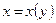, если в окрестности точки 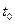определена функция 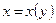и точка 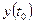является ее точкой минимума (максимума). Исследование точек минимума (максимума) функции 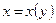осуществляется, как правило, исходя из определения при исследовании функци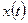й и 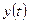. При этом 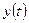является монотонной функций, а функция 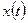имеет минимум (максимум).

Точка 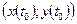называется точкой возврата кривой, если в окрестности точки 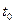определены функци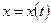и и 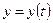, точка 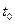является точкой экстремума обеих функций и совпадают односторонние касательные к кривой пр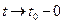и и 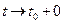. Так как функция 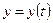имеет экстремум в этой точке, то .

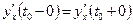5. Выпуклость функции вверх и вниз. Точки перегиба

Направление выпуклости кривой определяется на участках существования функции 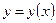аналогично случаю исследования функций по знаку второй производной, вычисляемой по формуле дифференцирования функции, заданной параметрически: .

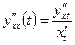Точки перегиба кривой определяются на участках параметра 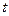, где существует функция 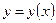и исследуется аналогично случаю функции.

Дата добавления: 2019-11-16; просмотров: 107; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 4 Следующая ⇒

Мы поможем в написании ваших работ!