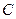Дифференцирование функции, аналитическое выражение которой содержит модуль
Содержание
Построение графиков функций . . . . . . . . . . . .
1. План исследования функции при построении графика . .
2. Основные понятия и этапы исследования функции . . . .
1. Область определения функции  и множество
значений функции и множество
значений функции  . Специальные свойства
функции . . . . . . . . . . . . . . . . . . . . . . . . . . .
2. Исследование асимптот . . . . . . . . . . . . . . . . .
2.1. Вертикальные асимптоты . . . . . . . . . . . . . . .
2.2. Наклонные (горизонтальные) асимптоты . . . . . . .
2.3. Методы исследования невертикальных асимптот . .
2.4. Взаимное расположение графика функции
и его асимптоты . . . . . . . . . . . . . . . . . . . . . . .
3. Построение эскиза графика функции . . . . . . . . . .
4. Участки возрастания и убывания функции
Точки минимума и максимума . . . . . . . . . . . . . . .
5. Выпуклость функции вверх и вниз
Точки перегиба . . . . . . . . . . . . . . . . . . . . . . .
3. Дифференцирование функции, аналитическое
выражение которой содержит модуль . . . . . . . . . . . . .
4. Основные требования к результатам исследования
и построению графика . . . . . . . . . . . . . . . . . . . . .
5. Примеры исследования функций и построения
графиков функций . . . . . . . . . . . . . . . . . . . . . . .
Пример 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Пример 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Пример 3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Пример 4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Пример 5 . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Пример 6 . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Построение кривых . . . . . . . . . . . . . . . . . . . .
1.План исследования и построения кривых . . . . . . . . . .
2. Основные понятия и этапы исследования кривой . . . . .
1. Исследование функций . Специальные свойства
функции . . . . . . . . . . . . . . . . . . . . . . . . . . .
2. Исследование асимптот . . . . . . . . . . . . . . . . .
2.1. Вертикальные асимптоты . . . . . . . . . . . . . . .
2.2. Наклонные (горизонтальные) асимптоты . . . . . . .
2.3. Методы исследования невертикальных асимптот . .
2.4. Взаимное расположение графика функции
и его асимптоты . . . . . . . . . . . . . . . . . . . . . . .
3. Построение эскиза графика функции . . . . . . . . . .
4. Участки возрастания и убывания функции
Точки минимума и максимума . . . . . . . . . . . . . . .
5. Выпуклость функции вверх и вниз
Точки перегиба . . . . . . . . . . . . . . . . . . . . . . .
3. Дифференцирование функции, аналитическое
выражение которой содержит модуль . . . . . . . . . . . . .
4. Основные требования к результатам исследования
и построению графика . . . . . . . . . . . . . . . . . . . . .
5. Примеры исследования функций и построения
графиков функций . . . . . . . . . . . . . . . . . . . . . . .
Пример 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Пример 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Пример 3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Пример 4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Пример 5 . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Пример 6 . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Построение кривых . . . . . . . . . . . . . . . . . . . .
1.План исследования и построения кривых . . . . . . . . . .
2. Основные понятия и этапы исследования кривой . . . . .
1. Исследование функций  и и 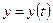 . . . . . . .
2. Использование результатов исследования . . . . . . .
2. Использование результатов исследования  . .
2.1. Вертикальные асимптоты кривой . . . . . . . . . . .
2.2. Наклонные (горизонтальные) асимптоты кривой . .
3. Анализ результатов и построение эскиза
графика функции . . . . . . . . . . . . . . . . . . . . . .
4. Участки возрастания и убывания кривой
Точки минимума и максимума функций . .
2.1. Вертикальные асимптоты кривой . . . . . . . . . . .
2.2. Наклонные (горизонтальные) асимптоты кривой . .
3. Анализ результатов и построение эскиза
графика функции . . . . . . . . . . . . . . . . . . . . . .
4. Участки возрастания и убывания кривой
Точки минимума и максимума функций
 и и 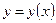 , точки возврата кривой . . . . . . .
5. Выпуклость функции вверх и вниз. Точки перегиба . .
3. Построение параметрически заданных кривых . . . . . .
Пример 7 . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Пример 8 . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Пример 9 . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Задачи для самостоятельного решения . . . . . .
Ответы . . . . . . . . . . . . . . . . . . . . . . . . . . . . , точки возврата кривой . . . . . . .
5. Выпуклость функции вверх и вниз. Точки перегиба . .
3. Построение параметрически заданных кривых . . . . . .
Пример 7 . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Пример 8 . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Пример 9 . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Задачи для самостоятельного решения . . . . . .
Ответы . . . . . . . . . . . . . . . . . . . . . . . . . . . .
| 5 5 5 5 6 6 6 6 9 11 11 14 17 18 20 20 24 29 32 36 40 44 44 44 44 45 45 45 46 46 48 49 49 54 58 63 66 |
|
|
|
Построение графиков функций
План исследования функции при построении графика
1. Найти область определения функции. Часто полезно учесть множество значений функции. Исследовать специальные свойства функции: четность, нечетность; периодичность, свойства симметрии.
|
|
|
2. Исследовать асимптоты графика функции: вертикальные, наклонные. Проанализировать взаимное расположение графика функции и его наклонных (горизонтальных) асимптот.
3. Построить эскиз графика.
4. Найти участки монотонности функции: возрастание и убывание. Найти экстремумы функции: минимумы и максимумы.
Найти односторонние производные в точках разрыва производной функции и в граничных точках области определения функции (если односторонние производные существуют).
5. Найти промежутки выпуклости функции и точки перегиба.
2. Основные понятия и этапы исследования функции
1. Область определения функции  и множество значений функции
и множество значений функции  . Специальные свойства функции
. Специальные свойства функции
Указать область определения функции, на оси абсцисс отметить ее граничными точками и выколотыми точками, указать абсциссы этих точек. Нахождение области определения функции приводить не обязательно.
Множество значений функции находить не обязательно. Легко исследуемые свойства множества значений: неотрицательность, ограниченность снизу или сверху и т.п., используются для построения эскиза графика, контроля результатов исследования и правильности построения графика.
|
|
|
График четной функции симметричен относительно оси ординат  . График нечетной функции симметричен относительно начала координат. Четные и нечетные функции исследуют на положительной половине области определения.
. График нечетной функции симметричен относительно начала координат. Четные и нечетные функции исследуют на положительной половине области определения.
Периодическую функцию исследуют на одном периоде, а график приводят на 2-3-х периодах.
2. Исследование асимптот
2.1. Вертикальные асимптоты
Определение 1. Прямая  называется вертикальной асимптотой графика функции
называется вертикальной асимптотой графика функции  , если выполнено хотя бы одно из условий:
, если выполнено хотя бы одно из условий:  [1] или
[1] или 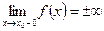 .
.
2.2. Наклонные (горизонтальные) асимптоты
Определение 2. Прямая  называется (невертикальной) асимптотой графика функции
называется (невертикальной) асимптотой графика функции  при
при 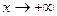 , если
, если 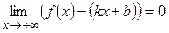 .
.
Из определения асимптоты при 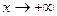 следует, что
следует, что  ,
,  . Вычисляя соответствующие пределы, получаем уравнение асимптоты
. Вычисляя соответствующие пределы, получаем уравнение асимптоты 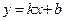 .
.
Аналогичное утверждение справедливо и в случае, когда 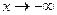 .
.
Если 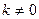 , то асимптота называется наклонной. Если
, то асимптота называется наклонной. Если  , то асимптота
, то асимптота 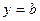 называется горизонтальной.
называется горизонтальной.
Аналогично вводятся понятия наклонной и горизонтальной асимптоты графика функции  при
при 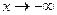 .
.
2.3. Методы исследования невертикальных асимптот
Исследование асимптот при 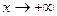 и при
и при 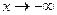 как правило проводят отдельно.
как правило проводят отдельно.
В некоторых частных случаях возможно совместное исследование асимптот при  и при
и при 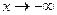 , например, для
, например, для
|
|
|
1) рациональных функций;
2) четных и нечетных функций, для графиков которых исследование можно проводить на части области определения.
Метод выделения главной части. Для нахождения асимптоты выделяем главную часть функции при 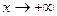 . Аналогично при
. Аналогично при 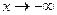 .
.
Главную часть дробно рациональной функции удобно находить, выделяя целую часть дроби:
Пример 1. Найти наклонные асимптоты графика функции  .
.
►  . Так как
. Так как  при
при  , то прямая
, то прямая  является искомой асимптотой. ◄
является искомой асимптотой. ◄
Главную часть иррациональной функции при решении практических примеров удобно находить используя методы представления функции формулой Тейлора при  .
.
Пример 2. Найти наклонную асимптоту графика функции 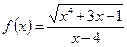 при
при  .
.
►Так как
 при
при 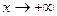 , то прямая
, то прямая 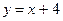 является искомой асимптотой. ◄
является искомой асимптотой. ◄
Главную часть иррациональных функций вида 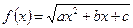 и
и  удобно находить соответственно методом выделения полного квадрата или полного куба подкоренного выражения.
удобно находить соответственно методом выделения полного квадрата или полного куба подкоренного выражения.
Пример 3. Найти наклонные асимптоты графика функции  при
при  и
и  .
.
►В подкоренном выражении выделим полный квадрат
 . Так как график функции
. Так как график функции 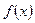 симметричен относительно прямой
симметричен относительно прямой  и
и  , то
, то 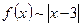 при
при  . Значит, прямая
. Значит, прямая 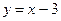 является асимптотой при
является асимптотой при 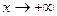 , а прямая
, а прямая  — асимптотой при
— асимптотой при  . ◄
. ◄
Для нахождения асимптот можно использовать метод выделения главной части.
Пример 4. Найти асимптоты графика функции  .
.
►Так как
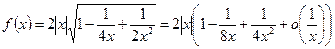 , то функция имеет асимптоту
, то функция имеет асимптоту  при
при 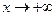 и асимптоту
и асимптоту 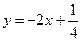 при
при  .◄
.◄
Для трансцендентных функций приемлемы оба метода исследования асимптот при решении практических примеров.
Замечание 1. При исследовании асимптот иррациональных, трансцендентных функций, а также функций, аналитическое выражение которых содержит модуль, целесообразно рассматривать два случая: 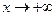 и
и  . Совместное исследование асимптот при
. Совместное исследование асимптот при 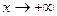 и при
и при 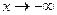 может привести к ошибкам в исследовании. При нахождении пределов или главной части при
может привести к ошибкам в исследовании. При нахождении пределов или главной части при 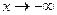 необходимо выполнить замену переменной
необходимо выполнить замену переменной  .
.
2.4. Взаимное расположение графика функции и его асимптоты
а) Если функция  имеет асимптоту при
имеет асимптоту при 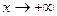 , дифференцируема и строго выпукла вниз на луче
, дифференцируема и строго выпукла вниз на луче  , то график функции лежит выше асимптоты (рис. 1.1).
, то график функции лежит выше асимптоты (рис. 1.1).
б) Если функция  имеет асимптоту при
имеет асимптоту при 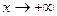 , дифференцируема и строго выпукла вверх на луче
, дифференцируема и строго выпукла вверх на луче  , то график функции лежит ниже асимптоты (рис. 1.2).
, то график функции лежит ниже асимптоты (рис. 1.2).


 в) Могут быть другие случаи поведения графика функции при стремлении к асимптоте. Например, возможно, что, график функции бесконечное число раз пересекает асимптоту (рис. 1.3 и 1.4).
в) Могут быть другие случаи поведения графика функции при стремлении к асимптоте. Например, возможно, что, график функции бесконечное число раз пересекает асимптоту (рис. 1.3 и 1.4).

Аналогичное утверждение справедливо и при 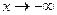 .
.
До исследования свойств выпуклости графика функции взаимное расположения графика функции и его асимптоты можно определить по знаку  в методе выделения главной части.
в методе выделения главной части.
Пример 5. Определить взаимное расположение графика функции  и его асимптот.
и его асимптот.
►  . Так как
. Так как 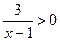 при
при 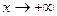 , то график функции лежит выше асимптоты
, то график функции лежит выше асимптоты  . Так как
. Так как  при
при 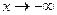 , то график функции лежит ниже асимптоты
, то график функции лежит ниже асимптоты  . ◄
. ◄
Пример 6. Определить взаимное расположение графика функции 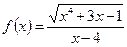 и его асимптоты при
и его асимптоты при 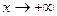 .
.
►Из равенства 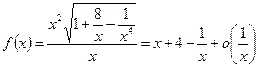 при
при 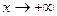 следует, что график функции лежит ниже асимптоты
следует, что график функции лежит ниже асимптоты 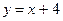 . ◄
. ◄
Пример 7. Определить взаимное расположение графика функции  и его асимптот.
и его асимптот.
► Так как 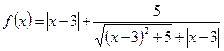 (см. пример 3), то график функции лежит выше асимптоты
(см. пример 3), то график функции лежит выше асимптоты 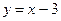 при
при  и при
и при 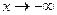 . ◄
. ◄
Пример 8. Определить взаимное расположение графика функции  и его асимптот.
и его асимптот.
► Так как  , то применяя формулу
, то применяя формулу 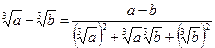 при
при  ,
,  , получаем
, получаем 
 . Эта разность положительна при
. Эта разность положительна при  и отрицательна при
и отрицательна при  . Поэтому при
. Поэтому при  график функции лежит ниже асимптоты
график функции лежит ниже асимптоты  , а при
, а при 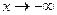 — выше асимптоты
— выше асимптоты  .◄
.◄
Метод вычисления пределов для исследования асимптот не позволяет оценить взаимное расположение графика функции и его асимптоты.
3. Построение эскиза графика функции
Для построения эскиза графика отмечаются вертикальные и наклонные асимптоты, точки пересечения графика функции с осями. Учитывая взаимное расположение графика функции и асимптот, строится эскиз графика. Если график функции лежит выше (ниже) асимптоты при  , то, предполагая, что существует такая точка
, то, предполагая, что существует такая точка  , что среди точек
, что среди точек  нет точек перегиба, получаем, что функция выпукла вниз(вверх), то есть к асимптоте. Аналогично можно прогнозировать направление выпуклости к асимптоте для вертикальных асимптот и для асимптоты при
нет точек перегиба, получаем, что функция выпукла вниз(вверх), то есть к асимптоте. Аналогично можно прогнозировать направление выпуклости к асимптоте для вертикальных асимптот и для асимптоты при  . Однако, как показывает приведенный выше пример функции
. Однако, как показывает приведенный выше пример функции  , такие предположения могут быть не верны.
, такие предположения могут быть не верны.
4. Участки возрастания и убывания функции. Точки минимума и максимума
Определение 3. Функция 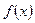 называется возрастающей (убывающей) на интервале
называется возрастающей (убывающей) на интервале  , если для любых
, если для любых  , таких что
, таких что  имеет место неравенство
имеет место неравенство 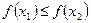 (
(  ).
).
Дифференцируемая на интервале  функция
функция 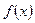 возрастает (убывает) на интервале
возрастает (убывает) на интервале  , тогда и только тогда, когда для любого
, тогда и только тогда, когда для любого 
 (
(  ).
).
Определение 4. Точка  называется точкой строгого локального максимума (минимума) функции
называется точкой строгого локального максимума (минимума) функции 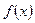 , если:
, если:
1) функция определена в некоторой окрестности точки  ;
;
2) существует окрестность  , такая что для любого
, такая что для любого  справедливо неравенство
справедливо неравенство  (
(  ).
).
Точки минимума и максимума называются точками экстремума функции  .
.
Необходимое условие экстремума. Если  — точка экстремума функции
— точка экстремума функции  , то в этой точке либо
, то в этой точке либо  , либо производная не существует.
, либо производная не существует.
Достаточные условия экстремума.
1. Пусть существует 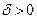 , такое что функция
, такое что функция  дифференцируема в проколотой
дифференцируема в проколотой  -окрестности точки
-окрестности точки  и непрерывна в точке
и непрерывна в точке  . Тогда,
. Тогда,
а) если ее производная меняет знак минус на плюс при переходе через точку 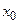 , т.е.
, т.е.  для любого
для любого  ,
,  для любого
для любого  , то
, то  — точка максимума функции
— точка максимума функции  ;
;
б) если ее производная меняет знак плюс на минус при переходе через точку 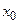 , т.е.
, т.е.  для любого
для любого  ,
,  для любого
для любого  , то
, то  — точка минимума функции
— точка минимума функции  .
.
Модельными примерами могут служить  (рис. 2.1) и
(рис. 2.1) и 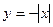 (рис.2.2).
(рис.2.2).


2. Если функция  дважды дифференцируема в точке
дважды дифференцируема в точке  ,
,  и
и  (
(  ), то точка
), то точка  является точкой максимума (минимума).
является точкой максимума (минимума).
Для запоминания достаточного условия удобно использовать модельные примеры:  (рис. 3.1) и
(рис. 3.1) и  (рис. 3.2) при
(рис. 3.2) при 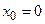 имеют максимум и минимум соответственно:
имеют максимум и минимум соответственно:


3. Пусть существует 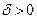 , такое что функция
, такое что функция  дифференцируема в проколотой
дифференцируема в проколотой  -окрестности точки
-окрестности точки  , непрерывна в точке
, непрерывна в точке  . Тогда,
. Тогда,
а) если существуют конечные или бесконечные правая и левая производные в точке 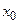 и
и  ,
,  , то
, то  является точкой минимума (рис.4.1).
является точкой минимума (рис.4.1).
б) если  ,
,  , то
, то  — точка максимума (рис. 4.2).
— точка максимума (рис. 4.2).


Замечание 2. Из теоремы Лагранжа о среднем следует, что, если существует окрестность  точки
точки 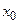 , такая что функция
, такая что функция  определена и непрерывна в окрестности
определена и непрерывна в окрестности  , дифференцируема в проколотой окрестности
, дифференцируема в проколотой окрестности  и существуют конечные или бесконечные пределы производных справа и слева
и существуют конечные или бесконечные пределы производных справа и слева 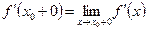 и
и  , то существуют и правая и левая производная
, то существуют и правая и левая производная  и
и  , и имеют место равенства
, и имеют место равенства  и
и 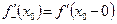 . Поэтому, при построении графиков функций для доказательства наличия экстремума в точке разрыва производной исследуемой функции как правило рассматривают пределы производных справа и слева. Предел производной справа (слева) равен тангенсу угла наклона касательной справа (слева) в точке экстремума.
. Поэтому, при построении графиков функций для доказательства наличия экстремума в точке разрыва производной исследуемой функции как правило рассматривают пределы производных справа и слева. Предел производной справа (слева) равен тангенсу угла наклона касательной справа (слева) в точке экстремума.
Замечание 3. Точка разрыва первого и второго рода функции  может быть точкой локального экстремума (рис. 5.1 и 5.2).
может быть точкой локального экстремума (рис. 5.1 и 5.2).


5. Выпуклость функции вверх и вниз. Точки перегиба
Определение 5. Непрерывная функция  называется выпуклой вверх (строго выпуклой вверх) на отрезке
называется выпуклой вверх (строго выпуклой вверх) на отрезке  , если для любых различных точек
, если для любых различных точек  и
и  отрезка
отрезка  выполняется неравенство
выполняется неравенство  .
.
Определение 6. Непрерывная функция  называется выпуклой вниз (строго выпуклой вниз) на отрезке
называется выпуклой вниз (строго выпуклой вниз) на отрезке  , если для любых различных точек
, если для любых различных точек  и
и  отрезка
отрезка  выполняется неравенство
выполняется неравенство
 .
.
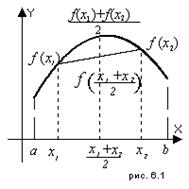
Из определений следует, что непрерывная функция  называется выпуклой вверх (строго выпуклой вверх) на отрезке
называется выпуклой вверх (строго выпуклой вверх) на отрезке  , если каждая точка любой хорды к графику функции
, если каждая точка любой хорды к графику функции  лежит не выше (ниже) графика
лежит не выше (ниже) графика  (рис. 6.1). Непрерывная функция
(рис. 6.1). Непрерывная функция  называется выпуклой вниз (строго выпуклой вниз) на отрезке
называется выпуклой вниз (строго выпуклой вниз) на отрезке  , если каждая точка любой хорды к графику функции
, если каждая точка любой хорды к графику функции  лежит не ниже (выше) графика
лежит не ниже (выше) графика  (рис. 6.2).
(рис. 6.2).

Достаточные условия выпуклости вверх и вниз функции  на отрезке: Пусть
на отрезке: Пусть  существует на отрезке
существует на отрезке  , а
, а  — на интервале
— на интервале 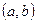 .
.
1. Если  (
(  )при всех
)при всех  , то функция выпукла вверх (строго выпукла верх) на отрезке
, то функция выпукла вверх (строго выпукла верх) на отрезке 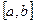 .
.
2. Если  (
(  ) при всех
) при всех  , то функция выпукла вниз (строго выпукла вниз) на отрезке
, то функция выпукла вниз (строго выпукла вниз) на отрезке  .
.
Определение 7. Точка  называется точкой перегиба функции
называется точкой перегиба функции  , если:
, если:
1. Функция  непрерывна в точке
непрерывна в точке  ;
;
2. Функция  имеет в точке
имеет в точке  конечную или бесконечную определенного знака производную;
конечную или бесконечную определенного знака производную;
3. Функция  при переходе через точку
при переходе через точку  меняет направление выпуклости, то есть существует
меняет направление выпуклости, то есть существует  , такое что на одном из интервалов
, такое что на одном из интервалов  ,
,  функция выпукла вверх, а на другом выпукла вниз.
функция выпукла вверх, а на другом выпукла вниз.
Определение 8. Точка  называется точкой перегиба графика функции
называется точкой перегиба графика функции  , если
, если  — точка перегиба функции
— точка перегиба функции  .
.
Необходимое условие перегиба в точке  .
.
Если  — точка перегиба функции
— точка перегиба функции  и функция
и функция  имеет в некоторой окрестности точки
имеет в некоторой окрестности точки  вторую производную, непрерывную в точке
вторую производную, непрерывную в точке  , то
, то  .
.
Достаточные условия перегиба в точке  .
.
1. Если функция  непрерывна в окрестности точки
непрерывна в окрестности точки  , имеет в точке
, имеет в точке  конечную или бесконечную определенного знака производную, а функция
конечную или бесконечную определенного знака производную, а функция  определена в проколотой окрестности точки
определена в проколотой окрестности точки  и меняет знак при переходе через эту точку, то
и меняет знак при переходе через эту точку, то  — точка перегиба функции
— точка перегиба функции  .
.
2. Если  , а
, а  , то
, то  — точка перегиба функции
— точка перегиба функции  .
.
В качестве модельных примеров рассмотрим функции 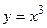 (рис. 7.1) и
(рис. 7.1) и  (рис. 7.2). Дополнительно рассмотрим еще два примера перегиба (рис. 7.3 и 7.4).
(рис. 7.2). Дополнительно рассмотрим еще два примера перегиба (рис. 7.3 и 7.4).



 Замечание 4. Если функция
Замечание 4. Если функция  дважды дифференцируема в окрестности точки
дважды дифференцируема в окрестности точки  , и
, и  — точка перегиба функции
— точка перегиба функции  , то график функции переходит с одной стороны касательной на другую. Обратное неверно.
, то график функции переходит с одной стороны касательной на другую. Обратное неверно.
Пример 9. Доказать, что, из того, что график функции  в точке
в точке  переходит с одной стороны касательной на другую не следует, что точка
переходит с одной стороны касательной на другую не следует, что точка  является точкой перегиба функции
является точкой перегиба функции  .
.
► Рассмотрим функцию  . В точке
. В точке  график функции имеет горизонтальную касательную, и переходит с одной стороны касательно на другую, но точка
график функции имеет горизонтальную касательную, и переходит с одной стороны касательно на другую, но точка  не является точкой перегиба функции
не является точкой перегиба функции  , так как не существует левой и правой окрестностей точки
, так как не существует левой и правой окрестностей точки  , в которых сохраняется направление выпуклости функции
, в которых сохраняется направление выпуклости функции  . ◄
. ◄
Дифференцирование функции, аналитическое выражение которой содержит модуль
1) При исследовании с помощью производной поведения графика функции, аналитическое выражение которой содержит модуль, удобно производить дифференцирование по правилу сложной функции, учитывая, что  во всех точках дифференцируемости функции
во всех точках дифференцируемости функции 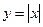 .
.
2) При дифференцировании функции вида  во всех точках дифференцируемости функции справедлива формула
во всех точках дифференцируемости функции справедлива формула  , так как производная функции сигнум равна нулю во всех точках дифференцируемости.
, так как производная функции сигнум равна нулю во всех точках дифференцируемости.
Пример 10. Найти первую и вторую производные функции 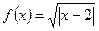 .
.
►  ,
,
 при
при  .◄
.◄
4. Основные требования к результатам исследования
и построению графика
1. Все результаты исследования функции следует обосновать в ходе решения. Все исследования функции, включая все необходимые вычисления: вычисления пределов функции, вычисления производных, решения уравнений, являются необходимой частью решения задачи на построение графика функции или кривой.
2. Все результаты должны быть получены точно. Необходимые приближенные вычисление привести в решении задачи.
3. Масштаб построения графика следует выбирать так, чтобы были отражены основные характерные моменты поведения графика функции.
4. На рисунке изобразить вертикаль[SVI1] ные и наклонные асимптоты, указать уравнения асимптот.
5. Обозначить точки минимума и максимума функции, указать их координаты.
6. Обозначить точки разрыва производной, указать их координаты. Изобразить односторонние касательные (если они существуют). В случае существования конечной односторонней производной указать тангенс угла наклона односторонней касательной.
7. Обозначить точки перегиба графика функции, указать их координаты. Указать точное значение производной или тангенс угла наклона касательной в точке перегиба. Изобразить касательную к графику функции в точке перегиба.
5. Примеры исследования функций и построения графиков функций.
Пример 1. Исследовать функцию  и построить ее график.
и построить ее график.
► Область определения функции  .
.
Асимптоты.
Вертикальная асимптота 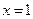 .
.
Для нахождения наклонной асимптоты можно использовать различные методы. Во-первых, уравнение асимптоты можно получить методом выделения главной части, как частное от деления  на
на  , выполнив его, например, "уголком", или используя представление
, выполнив его, например, "уголком", или используя представление  , или представляя
, или представляя  по формуле Тейлора в окрестности точки
по формуле Тейлора в окрестности точки 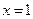 . Асимптотой графика функции при
. Асимптотой графика функции при  и при
и при  является прямая
является прямая  .
.
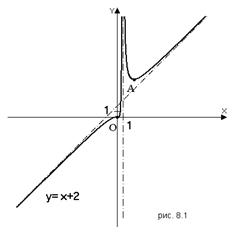
Строим эскиз. Изображаем оси координат и асимптоты. Из равенства  , следует, что при
, следует, что при  график функции стремится к асимптоте
график функции стремится к асимптоте  снизу, так как
снизу, так как  ; при
; при  график функции стремится к асимптоте
график функции стремится к асимптоте  сверху, так как
сверху, так как  . Можно предположить, что график функции при достаточно больших отрицательных значениях аргумента имеет направление выпуклости к асимптоте, то есть вверх.
. Можно предположить, что график функции при достаточно больших отрицательных значениях аргумента имеет направление выпуклости к асимптоте, то есть вверх.
При стремлении к асимптоте  слева функция стремится к
слева функция стремится к  . Можно предположить, что график функции в достаточно малой левой окрестности точки
. Можно предположить, что график функции в достаточно малой левой окрестности точки  является выпуклым вниз (к асимптоте).
является выпуклым вниз (к асимптоте).
При стремлении к асимптоте  справа функция стремится к
справа функция стремится к  . Можно предположить, что график функции в достаточно малой правой окрестности точки
. Можно предположить, что график функции в достаточно малой правой окрестности точки  также является выпуклым вниз (к асимптоте).
также является выпуклым вниз (к асимптоте).
Так как на промежутке  функция дифференцируема и меняет направление выпуклости, то на этом промежутке должна быть точка перегиба. Эскиз графика изображен на рис. 8.1.
функция дифференцируема и меняет направление выпуклости, то на этом промежутке должна быть точка перегиба. Эскиз графика изображен на рис. 8.1.
Найдем первую и вторую производные функции
 ;
; 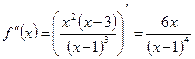 .
.
Анализ результатов исследования. Результаты исследования удобно объединить в виде таблицы. Первая колонка таблицы содержит все промежутки и особую точку  графика функции, а также точки, в которых равны нулю или не существуют первая или вторая производные.
графика функции, а также точки, в которых равны нулю или не существуют первая или вторая производные.

| 
| 
| Выводы | ||
| 
| 
| 
|  , асимптота , асимптота
| |
| 
| 
| 
| 
| точка локального минимума |

| 
| 
| 
| ||

| вертикальная асимптота | ||||

| 
| 
| 
| ||

| 
| 
| 
| 
| точка перегиба с горизонтальной касательной |

| 
| 
| 
|  , асимптота , асимптота
|
Замечание . При заполнении таблицы следует иметь в виду, что:
1) в таблицу мы вносим существенные для построения графика выводы, заполнение всех клеточек не обязательно;
2) если в таблицу вносим числовое значение, то оно должно быть точным, далее можно указать приближенное значение;
3) на этапе заполнения таблицы и построения графика целесообразно проверить согласованность полученных результатов исследования.
График функции изображен на рис. 8.2.
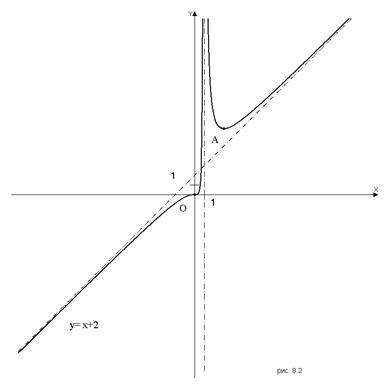
Пример 2. Исследовать функцию  и построить ее график.
и построить ее график.
► Область определения функции  .
.
Асимптоты.
Так как знаменатель функции  обращается в ноль при
обращается в ноль при  , то прямая
, то прямая  — вертикальная асимптота.
— вертикальная асимптота.
Так как  , то прямая
, то прямая  является асимптотой графика функции при
является асимптотой графика функции при  и при
и при  . При
. При  график функции лежит выше асимптоты, а при
график функции лежит выше асимптоты, а при  — ниже.
— ниже.
Построение эскиза. Изображаем асимптоты. При  график функции стремится к асимптоте
график функции стремится к асимптоте  снизу, так как
снизу, так как  . Можно предположить, что график функции при достаточно больших отрицательных значениях аргумента является выпуклым вверх.
. Можно предположить, что график функции при достаточно больших отрицательных значениях аргумента является выпуклым вверх.
При стремлении к асимптоте 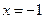 слева функция стремится к
слева функция стремится к  . Можно предположить, что график функции в некоторой левой полуокрестности точки
. Можно предположить, что график функции в некоторой левой полуокрестности точки 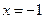 является выпуклым вверх (к асимптоте).
является выпуклым вверх (к асимптоте).
При стремлении к асимптоте 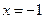 справа функция стремится к
справа функция стремится к  . Можно предположить, что график функции в некоторой правой полуокрестности точки
. Можно предположить, что график функции в некоторой правой полуокрестности точки 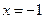 также является выпуклым вверх (к асимптоте).
также является выпуклым вверх (к асимптоте).
При  график функции стремится к асимптоте
график функции стремится к асимптоте  сверху, так как
сверху, так как  . Можно предположить, что график функции при достаточно больших значениях аргумента является выпуклым вверх. Так как на промежутке
. Можно предположить, что график функции при достаточно больших значениях аргумента является выпуклым вверх. Так как на промежутке  функция дифференцируема и меняет направление выпуклости, то на этом промежутке должна быть точка перегиба. Эскиз графика изображен на рис. 9.1.
функция дифференцируема и меняет направление выпуклости, то на этом промежутке должна быть точка перегиба. Эскиз графика изображен на рис. 9.1.

Найдем первую и вторую производные функции
 ;
; 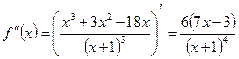 .
.
Анализ результатов исследования. Заполняя таблицу, учитываем, что в правой и левой окрестностях точки  , поведение графика функции различно.
, поведение графика функции различно.

| 
| 
| Выводы | ||
| 
| 
| 
|  , асимптота , асимптота
| |
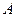
| 
| 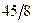
| 
| 
| точка локального минимума |

| 
| 
| 
| ||

| 
| 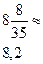
| 
| 
| точка перегиба,
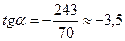
|

| 
| 
| 
| ||

| 
| 
| 
| 
| точка локального максимума |

| 
| 
| 
| ||

| 
| 
| 
|  , вертикальная асимптота , вертикальная асимптота
| |

| 
| 
| 
|  , вертикальная асимптота , вертикальная асимптота
| |

| 
| 
| 
| ||

| 
| 
| 
| 
| точка локального максимума |

| 
| 
| 
|  , асимптота , асимптота
|
Построение графика по результатам исследования
Замечание. Пункт приведен только для пояснения этапов анализа результатов исследования и построения графика функции.
На координатной плоскости изображаем вертикальную и наклонные асимптоты.
Так как при  график функции возрастает и имеет выпуклость вверх, то график стремится к наклонной асимптоте снизу. Возрастание продолжается до точки локального максимума
график функции возрастает и имеет выпуклость вверх, то график стремится к наклонной асимптоте снизу. Возрастание продолжается до точки локального максимума  . Далее график функции убывает и стремится к вертикальной асимптоте
. Далее график функции убывает и стремится к вертикальной асимптоте 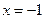 .
.
Так как график функции является выпуклым вверх, то функция возрастает справа от вертикальной асимптоты 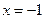 до точки максимума
до точки максимума  , а затем убывает до точки перегиба
, а затем убывает до точки перегиба  . Тангенс угла наклона касательной в точке перегиба
. Тангенс угла наклона касательной в точке перегиба  . На оставшемся промежутке график функции является выпуклым вниз.
. На оставшемся промежутке график функции является выпуклым вниз.
Функция убывает до точки локального минимума 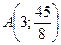 , а затем функция возрастает, стремясь к асимптоте сверху. График функции изображен на рис. 9.2.
, а затем функция возрастает, стремясь к асимптоте сверху. График функции изображен на рис. 9.2.

Пример 3. Исследовать функцию  и построить ее график.
и построить ее график.
► Область определения функции
 .
.
Функция является нечетной, исследование проводим на положительной полуоси,  .
.
Асимптоты.
Знаменатель функции обращается в ноль при  , поэтому прямая
, поэтому прямая  — вертикальная асимптота.
— вертикальная асимптота.
Так как  , то прямая
, то прямая 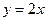 является асимптотой графика функции при
является асимптотой графика функции при  и при
и при  .
.
Анализ взаимного расположения графика функции и его асимптот аналогичен примеру 2.
Строим эскиз (рис.10.1). В левой полуплоскости эскиз строим по симметрии для нечетной функции.

Найдем первую и вторую производные
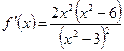 ;
;  .
.
Анализ результатов исследования. Результаты исследования объединим в виде таблицы.
Заполняя таблицу, учитываем, что в правой и левой окрестностях точки  , поведение графика функции различно.
, поведение графика функции различно.

| 
| 
| выводы | ||

| 
| 
| 
|  , асимптота , асимптота
| |
| 
| 
| 
| 
| точка минимума |

| 
| 
| 
| ||

| 
| 
| 
| вертикальная асимптота | |

| 
| 
| 
| ||

| 
| 
| 
| ||

| 
| 
| 
| 
| точка перегиба с горизонтальной касательной |
Используя свойство нечетности функции, получаем:
 — точка максимума.
— точка максимума.
График функции изображен на рис. 10.2.

Пример 4. Исследовать функцию 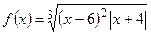 и построить ее график.
и построить ее график.
► Область определения функции 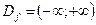 . Значения функции неотрицательны,
. Значения функции неотрицательны,  .
.
Асимптоты.
Вертикальных асимптот нет.
Наклонные асимптоты для иррациональной функции находим методом выделения главной части, дополнительный член представления находим для определения взаимного расположения графика и асимптоты.
Так как

 при
при  , то прямая
, то прямая  является асимптотой графика функции при
является асимптотой графика функции при  , график лежит ниже асимптоты. Аналогично, из равенства
, график лежит ниже асимптоты. Аналогично, из равенства

 при
при  , следует, что прямая
, следует, что прямая  является асимптотой графика функции при
является асимптотой графика функции при  , график лежит ниже асимптоты, так как
, график лежит ниже асимптоты, так как  .
.
Функция неотрицательна и  , а в других точках положительна, поэтому
, а в других точках положительна, поэтому  , и
, и  — точки локального минимума. Без дополнительного исследования с помощью производной или представления функции формулой Тейлора в окрестности этих точек мы не можем для иррациональной функции описать ее поведение в окрестности точек минимума. Поэтому на эскизе (рис. 11.1) мы опускаем малые окрестности этих точек.
— точки локального минимума. Без дополнительного исследования с помощью производной или представления функции формулой Тейлора в окрестности этих точек мы не можем для иррациональной функции описать ее поведение в окрестности точек минимума. Поэтому на эскизе (рис. 11.1) мы опускаем малые окрестности этих точек.

Найдем первую и вторую производные





 .
.
Анализ результатов исследования. Заполняя таблицу, учитываем, что в правой и левой окрестностях точек  , и
, и 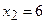 поведение графика функции различно.
поведение графика функции различно.

| 
| 
| Выводы | ||

| 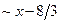
| 
| 
|  , асимптота выше графика , асимптота выше графика
| |
|
| 
|
| 
| 
| точка локального минимума с вертикальными односторонними касательными |

| 
| 
| |||

| 
| 
| 
| ||

| 
| 
| 
| 
| точка локального максимума |
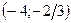
| 
| 
| 
| ||
|
| 
|
| 
| 
| локальный минимум с вертикальными односторонними касательными |

| 
| 
| |||

| 
| 
| 
|  , асимптота выше графика , асимптота выше графика
|
График функции изображен на рис. 11.2.
 ◄
◄
Пример 5. Исследовать функцию 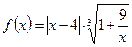 и построить ее график.
и построить ее график.
► Область определения функции  .
.
Асимптоты.
Так как  , а
, а  , то прямая
, то прямая  — вертикальная асимптота.
— вертикальная асимптота.
Наклонные асимптоты для иррациональной функции находим методом выделения главной части.
Имеем

 при
при  . Отсюда следует что прямая
. Отсюда следует что прямая  является асимптотой графика функции при
является асимптотой графика функции при 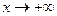 , причем график лежит ниже асимптоты. Аналогично из равенства
, причем график лежит ниже асимптоты. Аналогично из равенства

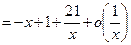 при
при  следует, что прямая
следует, что прямая  является асимптотой графика функции при
является асимптотой графика функции при  , причем график функции лежит ниже асимптоты, так как
, причем график функции лежит ниже асимптоты, так как 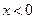 .
.
В достаточно малой правой окрестности нуля функция стремиться к 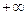 , можно предположить, что функция выпукла вниз. В достаточно малой левой окрестности нуля функция стремится к вертикальной асимптоте на
, можно предположить, что функция выпукла вниз. В достаточно малой левой окрестности нуля функция стремится к вертикальной асимптоте на  , можно предположить, что функция выпукла вверх. При положительных аргументах функция положительна, если
, можно предположить, что функция выпукла вверх. При положительных аргументах функция положительна, если  . Исследование поведения иррациональной функции в окрестности точки минимума проведем позднее с помощью производной. На эскизе этот участок не отражаем.
. Исследование поведения иррациональной функции в окрестности точки минимума проведем позднее с помощью производной. На эскизе этот участок не отражаем.
Строим эскиз (рис. 12.1).

Найдем производные функции

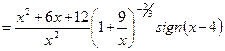 ;
; 

Анализ результатов исследования.
Заполняя таблицу, учитываем, что в правой и левой окрестностях точек  ,
,  и
и  поведение графика функции различно.
поведение графика функции различно.
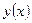
| 
| 
| Выводы | ||

| 
| 
| 
| 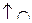 , асимптота выше графика , асимптота выше графика
| |
|
| 
|
| 
| 
| точка локального минимума, |

| 
| 
| |||

| 
| 
| 
| ||
|
| 
| 
| 
| 
| вертикальная асимптота |

| 
| 
| 
| ||

| 
| 
| 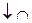
| ||

| 
| 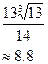
| 
| 
| точка перегиба, 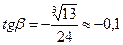
|

| 
| 
| 
| ||
|
| 
|
| 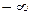
| 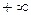
| точка перегиба с вертикальной касательной |

| 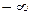
| 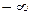
| |||

| 
| 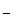
| 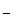
| 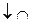 , асимптота выше графика , асимптота выше графика
|
График функции изображен на рис. 12.2.

Пример 6. Исследовать функцию  и построить ее график.
и построить ее график.
► Область определения функции  .
.
Асимптоты.
Так как  , то прямая
, то прямая 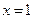 — вертикальная асимптота, при чем функция стремится к ней слева.
— вертикальная асимптота, при чем функция стремится к ней слева.
Наклонные асимптоты для иррациональной функции находим методом выделения главной части, для определения взаимного расположения графика и асимптоты представим функцию формулой Тейлора до  при
при 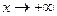 . Имеем
. Имеем


 при
при 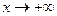 . Поэтому прямая
. Поэтому прямая  является асимптотой графика функции при
является асимптотой графика функции при 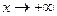 , график лежит выше асимптоты. Аналогично прямая
, график лежит выше асимптоты. Аналогично прямая  является асимптотой графика функции при
является асимптотой графика функции при  , причем график лежит ниже асимптоты, так как
, причем график лежит ниже асимптоты, так как  .
.
Заметим, что  .
.
Строим эскиз (рис. 13.1).

Дата добавления: 2019-11-16; просмотров: 297; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!


 ,
,