Методика вычисления полинома в форме Лагранжа
Рис.1. Методика вычисления полинома в форме Лагранжа
В качестве примера рассмотрим следующую практическую задачу. В рамках задачи известен набор шести значений, которые получены методом случайной выборки для различных моментов времени. Следует отметить, что данная выборка значений описывает функция 
на интервале [0, 10]. Необходимо построить многочлен в форме Лагранжа для представленного набора значений. С помощью интерполяционной формулывычислить приближенное значение функции в точке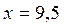 
, а также определить оценку погрешности результата вычислений.
Многочлен в форме Лагранжа, который строится на основании шести значений, представляет собой полином 5 степени. Результат построения полинома в форме Лагранжа показан в графическом виде.
Рис.2. Исходная функция и полином в форме Лагранжа, построенный по шести заданным точкам
С помощью найденного полинома можно определить значение функции в любой точке заданного интервала. Определение промежуточных значений величины по имеющемуся дискретному набору известных значений называется «интерполяцией». В соответствии с условиями задачи полином в форме Лагранжа в точке x=9,5 принимает следующее значение: L(9,5)= – 4,121. Из графика видно, что полученное значение не совпадает cо значением функции f(x) на величину абсолютной погрешности интерполяционной формулы Лагранжа.
Интерполяционный полином в форме Лагранжа часто оказывается удобным для проведения различных теоретических исследований в области вычислительной математики. Так, например, полином в форме Лагранжа используются для интерполяции, а также для численного интегрирования таблично-заданной функцией.
|
|
|
Задание 1
>> x=[-2 -4/3 0 4/3 2]
x =
-2.0000 -1.3333 0 1.3333 2.0000
>> y=2.*cos(pi*x/4)
y =
0.0000 1.0000 2.0000 1.0000 0.0000
Когда высчитываем полином на matlab значения, а значит и графики идеально совпадают.
>> Lnx=((x+2).*(x-0).*(x-4/3).*(x-2))/((-4/3+2).*(-4/3-0).*(-4/3-4/3).*(-4/3-2))+(2.*(x+2).*(x+4/3).*(x-4/3).*(x-2))/((0+2).*(0+4/3).*(0-4/3).*(0-2))+((x+2).*(x+4/3).*(x-0).*(x-2))/((4/3+2).*(4/3+4/3).*(4/3-0).*(4/3-2))
Lnx =
0 1 2 1 0
>> plot(x,y)
>> hold on
>> plot(x,Lnx,'g')
>> grid
А если вычислять в ручную на калькуляторе, то значения немного различаются
по-причине погрешности вычислений.
>> ln=0.0281*x.^4-0.6125*x.^2+2
ln =
-0.0004 0.9999 2.0000 0.9999 -0.0004
>> figure
>> plot(x,y)
>> plot(x,ln,'g')
>> hold on
>> plot(x,y)
>> grid
Задание 2
>> x=[-2 -1 0 1 2]
x =
-2 -1 0 1 2
>> y=3.^x
y =
0.1111 0.3333 1.0000 3.0000 9.0000
Когда высчитываем полином на matlab значения, а значит и графики идеально совпадают.
>> Lnx=( 0.1111.*(x+1).*(x-0).*(x-1).*(x-2))/((-2+1).*(-2+0).*(-2-1).*(-2-2))+(0.3333.*(x+2).*(x-0).*(x-1).*(x-2))/((-1+2).*(-1-0).*(-1-1).*(-1-2))+((x+2).*(x+1).*(x-1).*(x-2))/((0+2).*(0+1).*(0-1).*(0-2))+(3.*(x+2).*(x+1).*(x-0).*(x-2))/((1+2).*(1+1).*(1-0).*(1-2))+(9.*(x+2).*(x+1).*(x-0).*(x-1))/((2+2).*(2+1).*(2-0).*(2-1))
|
|
|
Lnx =
0.1111 0.3333 1.0000 3.0000 9.0000
А если вычислять в ручную на калькуляторе, то значения немного различаются
по-причине погрешности вычислений.
>> ln=0.074*x.^4+0.2963*x.^3+0.5926*x.^2+1.037*x+1
ln =
0.1100 0.3333 1.0000 2.9999 8.9988
Построение полиномов Ньютона первого и второго родов.
Интерполяционный многочлен в форме Ньютона – это математическая функция позволяющая записать полином n-степени, который будет соединять все заданные точки из набора значений, полученных опытным путём или методом случайной выборки с постоянным/переменным временным шагом измерений.
Дата добавления: 2020-01-07; просмотров: 179; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!