Методика вычисления полинома в форме Лагранжа
ЛАБОРАТОРНАЯ РАБОТА
« Построение полинома Лагранжа »
ДИСЦИПЛИНА: «Системы аналитических вычислений»
| Выполнил: студент гр. _________ _________________ (_____________________) (Подпись) (Ф.И.О.) Проверил: _________________ (_____________________) (Подпись) (Ф.И.О.) Дата сдачи (защиты): Результаты сдачи (защиты): - Балльная оценка: - Оценка: |
Мытищи , 201_
| Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Московский государственный технический университет имени Н.Э. Баумана (национальный исследовательский университет) Мытищинский филиал» (МФ МГТУ им. Н.Э. Баумана) |
ФАКУЛЬТЕТ _________________________________________
КАФЕДРА ____________________________________________
ЛАБОРАТОРНАЯ РАБОТА
« Построение полиномов Ньютона первого и второго родов »
ДИСЦИПЛИНА: «Системы аналитических вычислений»
| Выполнил: студент гр. _________ _________________ (_____________________) (Подпись) (Ф.И.О.) Проверил: _________________ (_____________________) (Подпись) (Ф.И.О.) Дата сдачи (защиты): Результаты сдачи (защиты): - Балльная оценка: - Оценка: |
Мытищи , 201_
Построение полинома Лагранжа.
Интерполяционный многочлен в форме Лагранжа – это математическая функция позволяющая записать полином n-степени, который будет соединять все заданные точки из набора значений, полученных опытным путём или методом случайной выборки в различные моменты времени с непостоянным временным шагом измерений.
|
|
|
Интерполяционная формула Лагранжа
В общем виде интерполяционный многочленв форме Лагранжа записывается в следующем виде:
где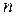 
˗ степень полинома 
;
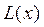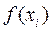˗ значение значения интерполирующей функции 
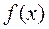в точке 
;
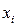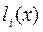˗ базисные полиномы (множитель Лагранжа), которые определяются по формуле:
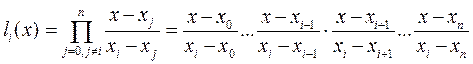
Так, например, интерполяционный многочленв форме Лагранжа, проходящий через три заданных точки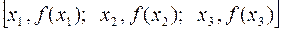 
, будет записываться в следующем виде:
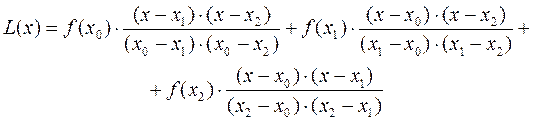
Многочлен в форме Лагранжа в явном виде содержит значения функций в узлах интерполяции, поэтому он удобен, когда значения функций меняются, а узлы интерполяции неизменны. Число арифметических операции, необходимых для построения многочлена Лагранжа, пропорционально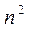 
и является наименьшим для всех форм записи. К недостаткам этой формы записи можно отнести то, что при построении полинома степени n+1 полностью теряется информация о предыдущем полиноме степени n, т.е. с изменением числа узлов приходится все вычисление выполнить заново.
|
|
|
Погрешность интерполяционного полинома в форме Лагранжа
Рассмотрим функцию f(x), которая непрерывна и дифференцируема на рассматриваемом отрезке [a, b]. Интерполяционный полином L(x) в форме Лагранжа принимает в точках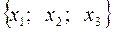 
заданные значения функции 
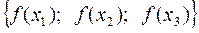. В остальных точках интерполяционный полином L(x) отличается от значения функции f(x) на величину остаточного члена, который определяет абсолютную погрешность интерполяционной формулы Лагранжа:
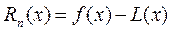
Абсолютную погрешность интерполяционной формулы Лагранжа определяют следующим образом:
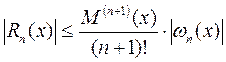
где n˗ степень полинома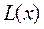 
Переменная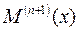 
представляет собой верхнюю границу значения модуля (n +1)-й производной функции f(x) на заданном интервале [a, b]
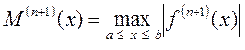
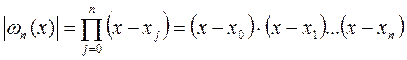
Погрешность интерполяции методом Лагранжа зависит от свойств функцииf(x), а также от расположения узлов интерполяции и точки x. В случае если погрешность не достигает нужной точности, то нужно разбить отрезок на части и интерполировать каждую часть в отдельности – кусочная интерполяция.
Выбор узлов интерполяции
С помощью корректного выбора узлов можно минимизировать значение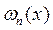 
в оценке погрешности, тем самым повысить точность интерполяции. Данная задача может быть решена с помощью многочлена Чебышева:
|
|
|
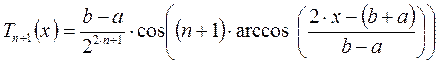
В качестве узлов следует взять корни этого многочлена, то есть точки:
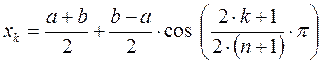
Методика вычисления полинома в форме Лагранжа
Алгоритм вычисления полинома в форме Лагранжа позволяет разделить задачи определения коэффициентов и вычисления значений полинома при различных значениях аргумента:
1. В качестве исходных данных задается выборка из n-точек, которая включает в себя значения функции и значения аргумента функции.
2. Выполняется вычисление полинома n-степени в форме Лагранжа по следующей формуле:
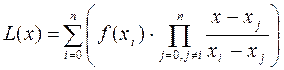
Алгоритм вычисления полинома в форме Лагранжа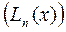 
представлен на рисунке 1.
Дата добавления: 2020-01-07; просмотров: 303; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!