Ускорения точек плоской фигуры.

⇐ ПредыдущаяСтр 7 из 8Следующая ⇒

Движение плоской фигуры в своей плоскости можно разложить на поступательное движение вместе с произвольно выбранной точкой, принимаемой за полюс, и вращательное движение вокруг этого полюса.

Следовательно, ускорение любой точки при плоском движении равно геометрической сумме двух ускорений: ускорения выбранного полюса, и ускорения, полученного данной точкой при ее вращательном движении вокруг полюса.

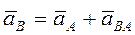Пусть известно ускорение точки А плоской фигуры тогда ускорение другой точки этой фигуры будет равно

где ускорение вращательного движения точки А вокруг точки В раскладывается на нормальное и касательное ускорения:

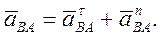
Касательное ускорение вращательного движения точки вокруг полюса направлено перпендикулярно отрезку АВ, соединяющему точку В с полюсом А, и равно

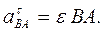
Нормальное ускорение направлено по отрезку ВА к полюсу А и равно

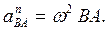
Окончательно, полное ускорение точки В равно геометрической сумме трех ускорений: ускорения выбранного полюса А, нормального и касательного ускорений вращательного движения точки В вокруг этого полюса:

План ускорений

Ускорения точек плоской фигуры могут быть определены графически с помощью плана ускорений. Этот метод позволяет находить ускорение точки плоской фигуры при условии, что известна траектория этой точки, ее скорость и ускорение одной из точек этой фигуры.

Пусть известно ускорение 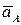точки А плоской фигуры, скорость 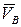точки В и ее траектория векторы на нем изображены без соблюдения масштабов).

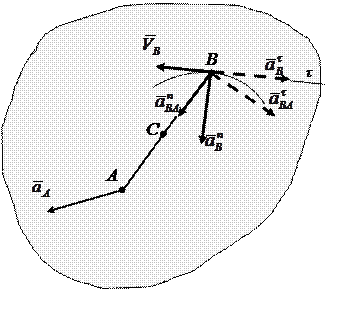Так как точка В совершает криволинейное движение, то ее ускорение раскладывается на нормальную и касательную составляющие:

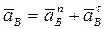. (а)

Оба ускорения известны по направлениям, ускорение 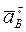направлено по касательной к траектории движения точки В, 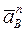- по главной нормали.

Модуль нормального ускорения определяется по формуле для криволинейного движения

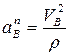где ρ – радиус кривизны траектории в данной точке.

Модуль касательного ускорения не определяется, так как закон движения точки В не задан. Следовательно, на основе анализа криволинейного движения полное ускорение точки найти не удается.

Проведем анализ плоского движения твердого тела, которому принадлежит точка В.

Плоское движение можно представить как сумму двух движений: поступательного вместе с точкой А и вращательного вокруг этой точки. В этом случае ускорение точки В выражается через ускорение точки А, модуль и направление которого известны, т.е.

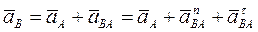, (б)

где 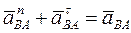и является полным ускорением точки В во вращательном движении плоской фигуры вокруг точки А.

В равенстве (б) все составляющие ускорения точки В известны по направлению. Ускорение точки А задано, ускорение 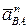направлено по прямой ВА к точке А, касательное ускорение 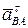- перпендикулярно прямой ВА.

Модуль ускорения 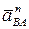определяется по формуле вращательного движения точки В вокруг точки А

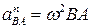где ω - угловая скорость плоской фигуры, ВА - радиус вращения.

Касательное ускорение 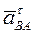по величине не определено.

Приравняем правые части выражений (а) и (б).

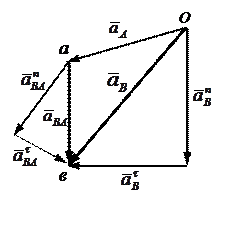Для графического определения ускорения точки В используем выражения (а) и (б).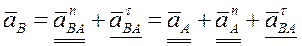

В этом равенстве одной чертой подчеркнуты векторы, у которых известно только направление, двумя чертами – векторы, для которых известны и направление и модуль.

Выберем неподвижную точку О за полюс и масштаб, в котором будем откладывать векторы ускорений. Отложим из точки О вектор 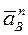и проведем к нему под прямым углом прямую, которая соответствует направлению вектора .

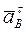Из этой же точки О отложим вектор 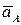. Из конца этого вектора отложим вектор 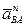и проведем к нему перпендикулярную прямую, которая определяет направление вектора 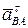. Точка в пересечения прямых, соответствующих направлениям векторов 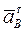и 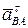, определяет конец вектора 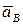. Соединим точки О и в (рис. 3.43) и получим в выбранном масштабе ускорение точки В.

Так как 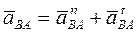, то, соединив, на графике точки а и в получим 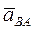полное ускорение вращательного движения точки В вокруг точки А.

Определим на графике ускорение точки С, которая делит расстояние между точками А и в пополам. Ускорение этой точки также можно выразить через ускорение точки А:

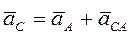Ускорения точек при вращательном движении пропорциональны радиусам вращения, поэтому

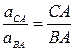Следовательно, для того, чтобы получить ускорение 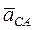, достаточно на графике разделить расстояние авпополам, полученную точку обозначим буквой с . Отрезок ас определяет величину ускорения 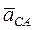. Соединяя точку с с точкой О получим на графике ускорение точки С плоской фигуры .

Задача. Построим план ускорений для механизма, в положении, указанном на рис. 3.45, если кривошип ОА вращается с постоянной угловой скоростью ω = 2 1/с, ОА = ВА =0,6м, СВ = 0,3 м, φ = 30⁰.

Решение. При равномерном вращении кривошипа касательное ускорение точки А будет равно нулю, поэтому полное ускорение равно нормальному ускорению,

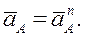
Вектор нормального ускорения направлен вдоль АО и равен

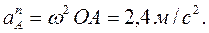
Ускорение точки В равно

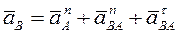. (а)

Ускорение точки В направлено горизонтально, так как ползун движется в горизонтальный направляющих, ускорение 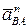направлено к точке по прямой АВ, и равно

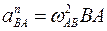где ω_АВ - угловая скорость шатуна АВ.

Угловую скорость звена АВ можно определить с помощью мгновенного центра скоростей который находится в точке Р пересечения перпендикуляров к скоростям в точках А и В.

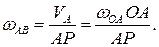
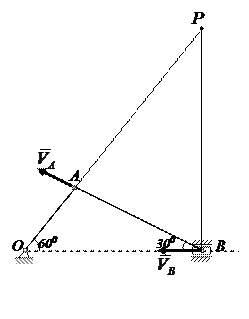
Из треугольника ОАВ АВ = ОА tg 60⁰,

Из треугольника АВР:

АР = АВ tq 60⁰ = OA tq ² 60⁰ =1,8 м.

Тогда

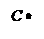
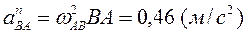Таким образом, в равенстве (а) векторы 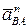и 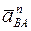известны по модулю и направлению, ускорения 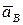и 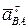только по направлению. Ускорение 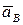направлено вдоль направляющих, ограничивающих движение ползуна, ускорение 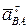- перпендикулярно АВ

Используя все полученные значения, строим план ускорений Выберем неподвижную точку О за начало ускорений всех точек звена АВ и установим масштаб для изображения ускорений. Проведем из точки О прямую, параллельную вектору 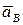. Отложим из этой же точки вектор 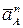, конец которого обозначим буквой а. Из точки а отложим вектор 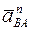(проведем прямую параллельную АВ), из конца этого вектора проведем прямую, параллельную вектору 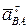(перпендикулярно отрезку АВ) и продолжим ее до пересечения с направлением вектора 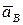. Полученную точку пересечения обозначим буквой в. Соединим точку О с точкой в, полученный отрезок OB в выбранном масштабе является ускорением 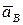точки В. Соединим точки а и в , полученный отрезок ав в выбранном масштабе представляет собой полное ускорение вращательного движения 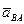точки В вокруг точки А.

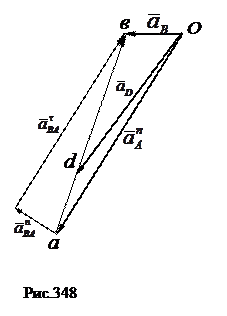Для того, чтобы определить ускорение любой точки D шатуна АВ, следует отрезок ав, представляющий собой вращательное ускорение точки В вокруг точки А, разделить точкой dв пропорции:

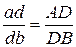Соединив точку d с точкой О, получим ускорение точки D шатуна АВ. Например, если AD = 0,25 AB, то, отложив из точки а отрезок ad = 0,25 ab, получим на графике точку d . Значит, отрезок Оd в выбранном масштабе является ускорением точки D шатуна.

4. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ.

4.1. Переносное, относительное и абсолютное движение.

Рассмотрим движение точки М относительно двух систем отсчета, одна из которых O ₁ x ₁ y ₁ z ₁ движется относительно другой, неподвижной, системы отсчета Oxyz .

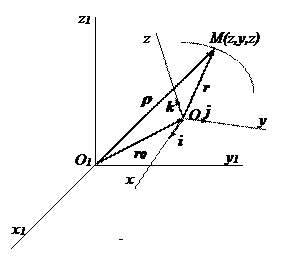Относительным называется движение точки М относительно подвижной системы отсчета O ₁ x ₁ y ₁ z ₁ .

Переносным называется движение, совершаемое подвижной системой отсчета Oxyz и всеми неизменно связанными с нею точками пространства относительно неподвижной системы отсчета.

Абсолютным называется движение точки по отношению к неподвижной системе отсчета O₁x₁y₁z₁ .

Всем кинематическим характеристикам, относящимся к относительному движению, присваивается индекс r, кинематическим характеристикам переносного движения–индекс е.

Относительной скоростью 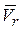называется скорость точки по отношению к подвижной системе отсчета.

Переносной скоростью 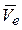называется скорость той точки, неизменно связанной с подвижной системой отсчета, с которой в данный момент совпадает точка М, относительно неподвижной системы отсчета.

Абсолютная скорость 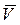- это скорость точки относительно неподвижной системы отсчета. Аналогично определяются относительное ускорение 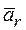, переносное ускорение 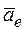и абсолютное ускорение .

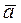Дата добавления: 2020-01-07; просмотров: 439; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 4 5 678 Следующая ⇒

Мы поможем в написании ваших работ!