История возникновения систем счисления
Первые и самые простые системы счисления были придуманы еще в древние времена. Так была придумана единичная система счисления: число в такой системе счисления представлялось в виде черточек. Сколько черточек – такое и значение числа. Очевидным недостатком единичной системы счисления является то, что запись больших чисел в ней весьма затруднительна. Для удобства палочки стали объединять в группы по 3, 5, 10 палочек, впоследствии каждой группе были присвоены свои знаки.
Более «продвинутая» система счисления была придумана в Древнем Египте (древнеегипетская десятичная система). Числа 1, 10, 100, 1000 и пр. Были обозначены специальными символами, некоторые из которых приведены на рис. 6.1.
| 
| 
|
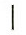
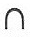
| 1 | 10 | 100 |
| Число 324: |
|
|
|
|
|
|
|
|
|
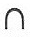
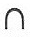
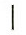
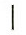
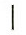
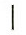
Рис. 6.1. Древнеегипетская десятичная система счисления
Одной из первых частично-позиционных систем счисления принято считать вавилонскую шестидесятеричную систему счисления. В ней всего 2 символа: ‚ , обозначающий единицу и ƒ, служащий для указания десятков. Числа от 1 до 59 записывались в непозиционной системе счисления. Так число 41 записывалось как ƒƒƒƒ‚. Начиная с числа 60 данная система счисления становилась позиционной, первым разрядом указывался символ, означающий 1 (‚). Так число 92 записывалось как ‚ƒƒƒ‚‚. Первоначально система имена много неоднозначностей, которые правились по мере развития системы счисления.
|
|
|
Позже были придуманы римская, греческая, славянская и многие другие системы счисления, а следом за ними и широко применяемые в настоящее время позиционные системы счисления (двоичная, десятичная и пр.).
Постановка задачи перевода чисел из одной системы счисления в другую
Любое конечное число 
в позиционной системе счисления 
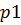может быть представлено в виде
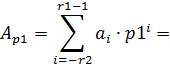
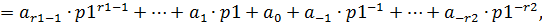
где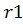 
, 
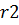– количество разрядов числа до и после запятой соответственно.
Число может быть представлено в системе счисления с основанием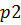 
в виде
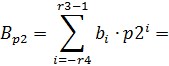
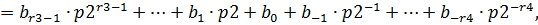
где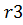 
, 
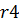– количество разрядов числа до и после запятой соответственно.
Ставится задача определения коэффициентов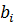 
представления числа 
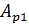в системе счисления с основанием .
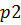Все рассмотренные ниже методы предназначены для преобразования чисел, представленных в позиционных системах счисления.
Методы перевода чисел из одной системы счисления в другую
Схема Горнера
В основу метода положена схема Горнера для решения алгебраических многочленов. Метод позволяет легко перевести число из 
-й системы счисления в десятичную
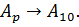
Реализуемые методом преобразования позволяют вычислить многочлен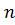 
-ой степени за 
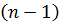операций сложения и 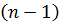операций умножения.
|
|
|
Общий вид многочлена 
-ой степени имеет вид
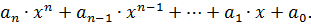(6.2)
Запись вида 5.2 может быть представлена в скобочной форме:
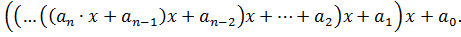(6.3)
Форму представления многочлена в виде 6.3 называют схемой Горнера.
Представление числа в позиционной системе счисления 6.1 может быть приведено к виду многочлена 6.2 заменой в последнем неизвестного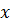 
на базис системы счисления числа . Схему Горнера для перевода числа из -й системы счисления в десятичную может быть представлена в виде
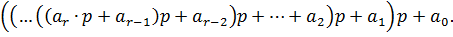(6.4)
Пример 6.1: Задано конечное число в системе счисления с основанием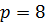 
: 
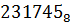. Требуется представить его в десятичной системе счисления используя схему Горнера.
.
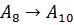Представим число 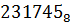в виде (5.1):
.
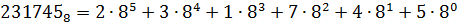Произведем преобразование выражения к виду 6.4 и выполним арифметические действия:
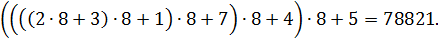
Производить вычисления выражения вида (6.4) удобно используя следующую табличную схему (рис. 6.2):
| 2 $ | + 3 $ | + 1 $ | + 7 $ | + 4 $ | + 5 $ | |
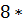
| 2 |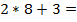 
| 
| 
| 
| 
|
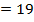
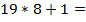
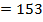
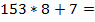
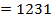
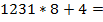
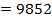
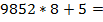
Рис. 6.2. Табличная реализация схемы Горнера для перевода числа из 
-й системы счисления в десятичную
Верхняя строка таблицы заполняется значениями разрядов числа от старших к младшим. На первом шаге старший разряд числа переписывается в первую ячейку второй строки таблицы (то есть под ячейкой старшего разряда). На каждом последующем шаге выполняются следующие действия: записанное в предыдущей ячейке число умножается на основание системы счисления и к нему прибавляется цифра следующего разряда числа; полученное значение записывается в следующую ячейку второй строки таблицы. Шаги вычислений продолжаются до тех пор, пока не будут заполнены все ячейки таблицы. Число, записанное в последней ячейке таблицы и будет результатом приведения искомого числа в десятичную систему счисления.
|
|
|
.
Схему Горнера можно использовать и для перевода вещественных чисел с нулевой целой частью.
Пример 6.2: Задано конечная дробь в системе счисления с основанием 
: 
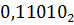. Требуется представить ее в десятичной системе счисления используя при переводе схему Горнера.
Представим число 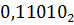в виде (5.1):
.
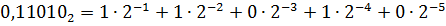Произведем преобразование выражения к виду (6.4) и выполним арифметические действия:
.
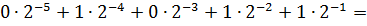
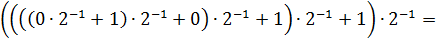
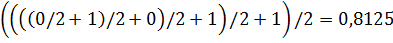Производить вычисления выражения вида (6.4) удобно используя следующую табличную схему (рис. 6.3):
| 0 $ | + 1 $ | + 0 $ | + 1 $ | + 1 $ | ||
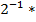
| 0 |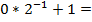 
| 
| 
| 
| 
|
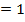
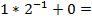
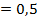
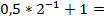
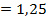
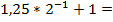
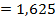
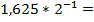
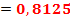
Рис. 6.3. Табличная реализация схемы Горнера для перевода числа из -й системы счисления в десятичную
|
|
|
Верхняя строка таблицы заполняется значениями разрядов числа от младших к старшим. На первом шаге младший разряд числа переписывается в первую ячейку второй строки таблицы (то есть под ячейкой младшего разряда). На каждом последующем шаге выполняются следующие действия: записанное в предыдущей ячейке число делится на основание системы счисления и к нему прибавляется цифра следующего разряда числа; полученное значение записывается в следующую ячейку второй строки таблицы. Шаги вычислений продолжаются до тех пор, пока не будут обработаны все разряды исходного числа. Полученное число делится на основание системы – это и будет результатом приведения искомого числа в десятичную систему счисления.
.
Схема Горнера может быть применена и для перевода неправильных дробей (то есть вещественных чисел с ненулевой целой частью). Для этого необходимо раздельно перевести целую часть числа и его дробную часть, а результат преобразования записать последовательно, отделив целую часть от дробной при помощи запятой.
Дата добавления: 2020-01-07; просмотров: 183; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!