Ограниченность однослойного персептрона
Методические указания
Нейронные сети и нейрокомпьютеры – это одно из направлений компьютерной индустрии, в основе которого лежит идея создания искусственных интеллектуальных устройств по образу и подобию человеческого мозга [1, 2]. Приведем основные сведения о принципах организации и функционирования человеческого мозга.
Мозг человека состоит из белого и серого вещества: белое – это тела нейронов, а серое – соединяющие их нервные волокна. Каждый нейрон состоит из трех частей: тела клетки, дендритов и аксона (рис. 1.1).
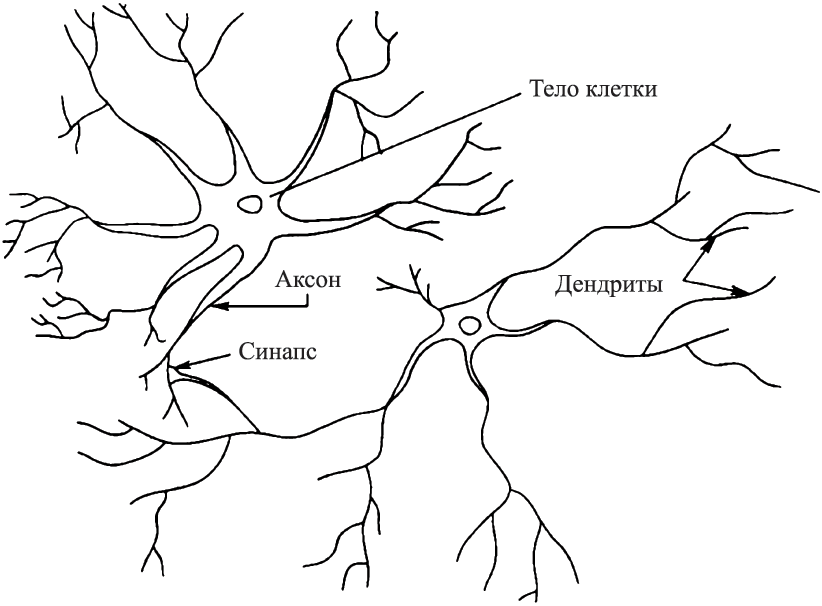
Рис. 1.1. Структура пары типичных нейронов
Нейрон получает информацию через свои дендриты, а передает ее дальше через аксон, разветвляющийся на конце на тысячи синапсов – нервных нитей, соединяющих нейроны между собой. Простейший нейрон может иметь до 10 000 дендритов, принимающих сигналы от других клеток. В человеческом мозге содержится приблизительно 1011 нейронов. Каждый нейрон связан с 103…104 другими нейронами. Таким образом, биологическая нейронная сеть, составляющая мозг человека, содержит 1014…1015 взаимосвязей.
Каждый нейрон может существовать в двух состояниях – возбужденном и невозбужденном. На вход его от других нейронов могут поступать сигналы возбуждения и сигналы торможения. Когда сигналы возбуждения превышают сигналы торможения на определенную величину, нейрон сам посылает электрический сигнал другим, соединенным с ним нейронам [1, 2].
|
|
|
Известно, что общее число нейронов в течение жизни человека практически не изменяется, т.е. мозг ребенка и взрослого человека содержат приблизительно одинаковое число нейронов. Отличие состоит в силе синаптических связей, т.е. в величине электрических проводимостей нервных волокон, соединяющих нейроны. Была высказана гипотеза о том, что все наши мысли, эмоции, знания, вся информация, хранящаяся в человеческом мозге, закодирована в виде сил синаптических связей. Процесс обучения человека, продолжающийся всю его жизнь, состоит в непрерывной корректировке значений этих синаптических связей.
Математическая модель нейрона
В 1943 году была опубликована статья Уоррена Мак-Каллока и Вальтера Питтса, в которой авторы выдвинули гипотезу математического нейрона – устройства, моделирующего нейрон мозга человека (рис. 1.2).
Рис. 1.2. Искусственный нейрон
Математический нейрон имеет несколько входов и один выход. Через входы, число которых обозначим N, математический нейрон принимает входные сигналы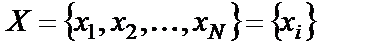 
, i = 1,2,…,N, которые суммирует, умножая каждый входной сигнал на некоторый весовой коэффициент 
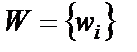, i = 1,2,…,N:
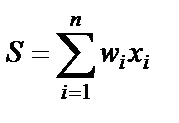. (1)
|
|
|
Выходной сигнал y может принимать одно из двух значений – нуль или единица и формируется по следующему правилу:
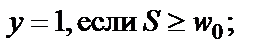(2)
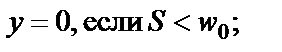(3)
где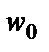 
– порог чувствительности нейрона.
Таким образом, математический нейрон представляет собой пороговый элемент с несколькими входами и одним выходом. Одни из входов оказывают возбуждающее воздействие, другие – тормозящее. Каждый математический нейрон имеет свое определенное значение порога. Если взвешенная сумма входных сигналов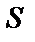 
не достигает порога чувствительности 
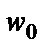, то нейрон не возбужден и его выходной сигнал равен нулю. Если же входные сигналы достаточно интенсивны и их сумма достигает порога чувствительности, то нейрон переходит в возбужденное состояние и на его выходе образуется сигнал 
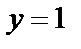. Весовые коэффициенты 
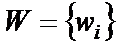, i =1,2,…,N имитируют электропроводность нервных волокон – силу синаптических связей между нейронами. Логическая функция (2) – (3) называется активационной функцией нейрона, на рис. 1.3 приведено ее изображение.
|
|
|
a б
Рис.1.3. Графики пороговых активационных функций:
а – симметричная, б - смещенная
Персептрон
У. Мак-Каллок и В. Питтс высказали идею о том, что сеть из математических нейронов в состоянии обучаться, распознавать образы, обобщать, т.е. она обладает свойствами человеческого интеллекта.
Эта идея была материализована в 1958 году Фрэнком Розенблаттом сначала в виде компьютерной программы, а затем в виде электронного устройства, моделирующего человеческий глаз. Это устройство представляло собой совокупность искусственных нейронов Мак-Каллока – Питтса и было названо персептроном. Устройство удалось обучить решению сложнейшей интеллектуальной задачи – распознаванию букв латинского алфавита.
Рассмотрим принцип действия персептрона на простом примере классификации цифр на четные и нечетные. Входные сигналы поступают от матрицы из 12 фотоэлементов, расположенных в виде четырех горизонтальных рядов по три фотоэлемента. На матрицу накладывается карточка с изображением цифры (например, это цифра 4). Если на фотоэлемент попадает какой-либо фрагмент цифры, то данный фотоэлемент вырабатывает сигнал в виде двоичной единицы, в противном случае – нуль. На рис. 1.4 первый фотоэлемент выдает сигнал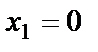 
, второй фотоэлемент – 
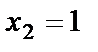и т.д. Цель обучения персептрона состоит в том, чтобы выходной сигнал y был равен единице, если на карточке была изображена четная цифра, и нулю, если цифра была нечетной.
|
|
|
Рис. 1.4.Схема распознавания нейроном четных и нечетных цифр
Эта цель достигается путем обучения персептрона. В процессе обучения корректируются весовые коэффициенты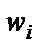 
таким образом, чтобы ошибка классификации для всех цифр была равна нулю или меньше заданной погрешности. Обучение происходит с использованием обучающих примеров, подобно обучению маленьких детей словам или буквам. Каждый пример предъявляется распознающему устройству неоднократно и при правильном распознавании типа цифры веса не меняются, а при наличии ошибки корректируются, пока не будет достигнута безошибочная классификация цифр. Самым простым и наиболее распространенным критерием окончания процесса обучения сети является достижение минимума среднеквадратичной ошибки при распознавании любой из десяти цифр:
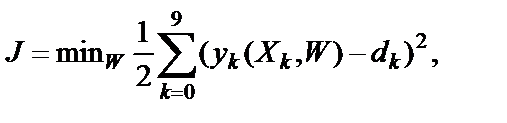(4)
где
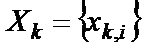, i = 1,12 – вектор входных сигналов, для каждой цифры – своя битовая строка;
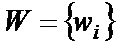, i = 1,12 – весовые коэффициенты, значения которых должны быть найдены в процессе обучения;
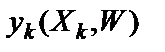– сигнал на выходе нейрона при подаче на его вход 
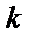-й цифры и значениях 
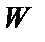весовых коэффициентов вычисляется по формулам (1) – (3);
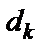– заданное значение выходного сигнала для 
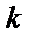-й цифры (если цифра четная, то 
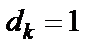, если цифра нечетная, то 
);
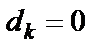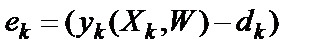– ошибка распознавания 
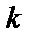-й цифры.
Одним из методов минимизации функции нескольких переменных является метод градиента. Градиент – это вектор, состоящий из частных производных анализируемой функции по ее аргументам. Он задает направление наискорейшего возрастания функции в некоторой точке. При поиске минимума функции необходимо двигаться в направлении, противоположном вектору градиента, или вдоль вектора, составляющего тупой угол с вектором градиента, что может быть выражено следующей формулой:
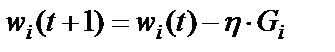, (5)
где
, 
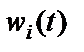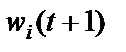– соответственно старое и новое значения весовых коэффициентов персептрона; 
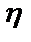– скорость обучения
, 
, 
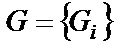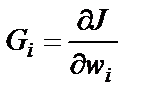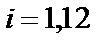– вектор градиента.
Для нейрона, описываемого формулами (1) – (3), вектор градиента будет иметь вид:
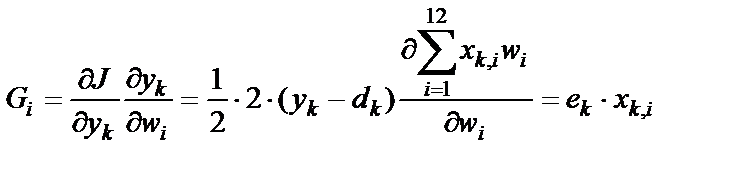, где k – номер примера, i – номер входного сигнала; ek – ошибка при предъявлении
k-го примера (k-й цифры).
Формула (5) подстройки весовых коэффициентов при предъявлении k -го примера принимает вид:
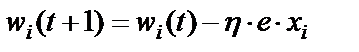. (6)
Первоначально весовым коэффициентам даются произвольные значения с помощью датчика случайных чисел.
Можно получить аналогичную итерационную формулу для подстройки порогового значения нейрона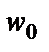 
, если учесть, что его можно интерпретировать как вес дополнительного входа 
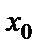, значение которого равно 
.
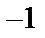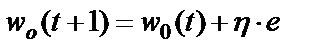, (7)
Схема алгоритма настройки весов приведена на рис. 1.5.
Рис.1.5. Схема алгоритма настройки весов
Возникает вопрос: «Всегда ли алгоритм обучения персептрона приводит к желаемому результату?». Ответ на этот вопрос дает теорема сходимости персептрона, формулируемая следующим образом.
Если существует множество значений весов, которые обеспечивают конкретное различение образов, то в конечном итоге алгоритм обучения персептрона приводит либо к этому множеству, либо к эквивалентному множеству, такому, что данное различение образов будет достигнуто.
Распознавание букв
Дальнейшее развитие идеи персептрона и алгоритмов обучения связано с усложнением его структуры и развитием функциональных свойств.
На рис. 1.6 приведена схема персептрона, предназначенного для распознавания букв русского алфавита. В отличие от предыдущей схемы такой персептрон имеет один слой из 33 нейронов, каждой букве соответствует свой нейрон. Полагается, что выход первого нейрона y1 должен быть равен единице, если персептрону предъявлена буква «А», и нулю для всех остальных букв. Выход второго нейрона y2 должен быть равен единице, если персептрону предъявлена буква «Б», и нулю во всех остальных случаях. И так далее до буквы «Я».
Рис. 1.6. Схема однослойного персептрона
Алгоритм обучения данного персептрона приведен на рис. 1.7.
Рис. 1.7. Схема алгоритма обучения однослойного персептрона
Корректировка весовых коэффициентов персептрона и пороговых значений нейронов производится по формулам (9), (10), полученным путем вычисления вектора градиента от функции:
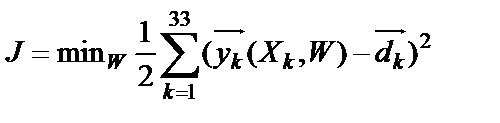. (8)
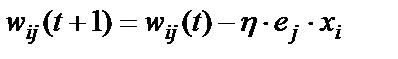, i=1,N; j=1,M (9)
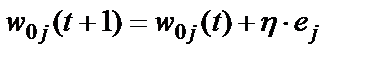, j=1,M (10)
Здесь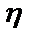 
– скорость обучения, 
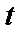– номер итерации.
Расширить возможности персептрона можно, если допустить, что входные и выходные сигналы являются не бинарными последовательностями, а аналоговыми (непрерывными сигналами). Такое обобщение персептрона было сделано учеными Уидроу и Хоффом [1, 2]. Они вместо ступенчатой ввели нелинейную функцию активации
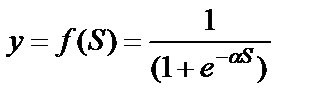, (11)
называемую сигмоидом (см. рис. 1.8). Здесь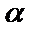 
– положительная константа, от значения которой зависит крутизна сигмоиды; 
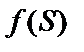– обозначение произвольной активационной функции.
Рис. 1.8. Активационная функция – сигмоида
Выходное значение нейрона лежит в диапазоне [0,1]. Ценные свойства активационной функции (11): сигмоида обеспечивает непрерывную аппроксимацию классической пороговой функции; дифференцируема на всей оси абсцисс и имеет простое выражение для ее производной, что используется в алгоритмах обучения. Она обладает свойством усиливать малые сигналы лучше, чем большие, что предотвращает насыщение от больших сигналов.
Известно также большое количество других разновидностей активационных функций [1, 2].
Рассмотрим, как изменятся формулы (8) – (10) настройки весов в методе градиентного спуска при новой активационной функции (11) при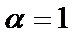 
.
Решается задача минимизации функции:
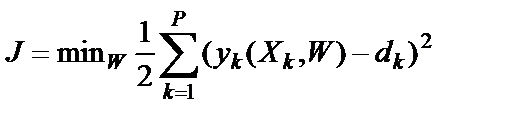, (12)
где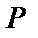 
– число обучающих примеров;
Метод градиентного спуска для каждого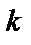 
-го обучающего примера описывается следующими итерационными формулами:
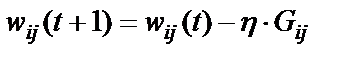, (13)
где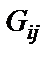 
– вектор градиента функции (12) в некоторой точке
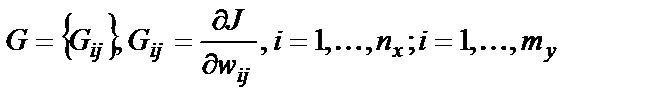, (14)
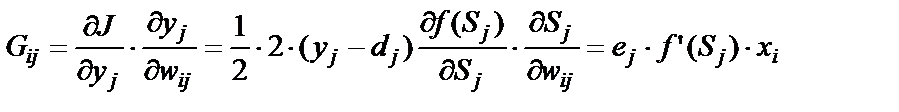, (15)
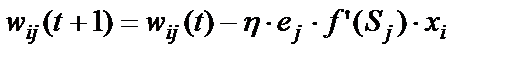. (16)
Формула (16) получена для нейронов с активационными функциями любого вида. Если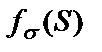 
– сигмоида (11), то ее производная равна
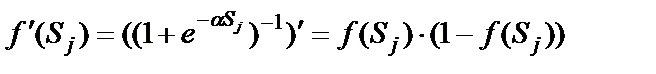. (17)
В результате формула (16) корректировки весов примет вид:
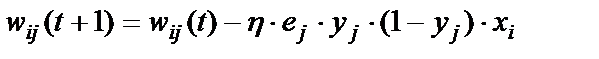, (18)
где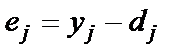 
.
Метод градиентного спуска имеет линейную скорость сходимости, а также резкое замедление оптимизационного процесса в окрестности точки оптимального решения, что делает его малоэффективным. Благодаря своей простоте этот алгоритм остается одним из наиболее распространенных.
Ограниченность однослойного персептрона
Класс решаемых персептронами задач расширялся. Делались попытки применения персептронов в задачах прогнозирования, таких как предсказание погоды и курсов акций. По мере расширения фронта научных исследований появились трудности. Оказалось, что многие задачи персептрон решить не мог. Назрела необходимость создания теоретической базы персептронов [1, 2].
В книге «Персептроны» М. Минского и С. Пайперта математически строго было доказано, что использовавшиеся в то время однослойные персептроны в принципе не способны решать многие простые задачи, например, задачу реализации логической операции «Исключающее ИЛИ» [3].
Позже было предложено усложнить структуру персептронов, использовать два слоя нейронов. Проблему «Исключающее ИЛИ» удалось решить с помощью двухслойного персептрона. Советским ученым С.О. Мкртчяном [4] был разработан специальный математический аппарат, позволяющий без обучения строить многослойные персептроны, моделирующие любые булевы функции.
Таким образом, было показано, что многослойные нейронные сети (рис. 1.9) расширяют класс задач, решаемых персептронами, но не было конечной детерминированной процедуры для настройки весовых коэффициентов такой сложной нейронной сети.
Только в 1986 году в работе Румельхарта, Хилтона и Вильямса был предложен эффективный алгоритм обучения многослойных персептронов, известный под именем алгоритма обратного распространения ошибки [1, 2].
Рис. 1.9. Многослойная нейронная сеть
Дата добавления: 2019-11-16; просмотров: 437; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!