Алгоритм обратного распространения ошибки
Дискретный динамический процесс как модель нейронной сети
Рассмотрим постановку задачи подстройки весовых коэффициентов многослойной нейронной сети как задачу оптимального управления дискретным динамическим процессом.
Пусть
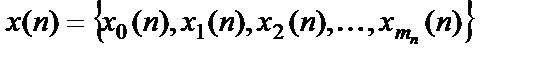– сигнал на выходе n-го слоя сети, mn – число нейронов в слое n; 
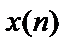– вектор-строка; 
– вектор-столбец; 
;
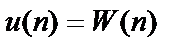– матрица весовых коэффициентов размером 
n-го слоя сети;
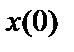– сигналы, подаваемые на вход нейронной сети;
n = 1, 2, …, N; N – число слоев нейронной сети;
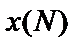– сигнал на выходе нейронной сети;
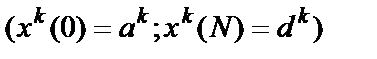, k = 1, 2, …, P – обучающие примеры: при
k-м входном сигнале 
на выходе сети необходимо обеспечить сигнал 
путем выбора значений весовых коэффициентов W.
Тогда задача настройки нейронной сети может быть сформулирована следующим образом.
Найти такие значения оптимального управления 
,
n = 1, 2, …, N, при которых будут выполнены следующие ограничения:
; (19)
– активационная функция; 
– знак умножения;
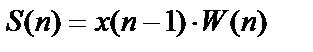– вектор сумм взвешенных сигналов для n-го слоя нейронной сети; n = 1, 2, …, N
и критерий качества процесса достигнет своего минимального значения
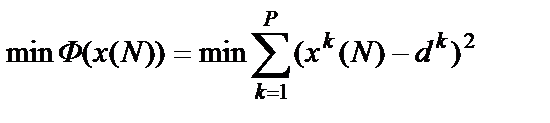(20)
,n = 1, 2, …, N.
Сопряженная система
Система (20) называется прямой системой уравнений. Она используется для получения сигнала на выходе нейронной сети при заданных значениях весовых коэффициентов W и известном входном сигнале 
.
|
|
|
Наряду с прямой системой важную роль играет сопряженная (двойственная) система, которая определяется соотношениями:
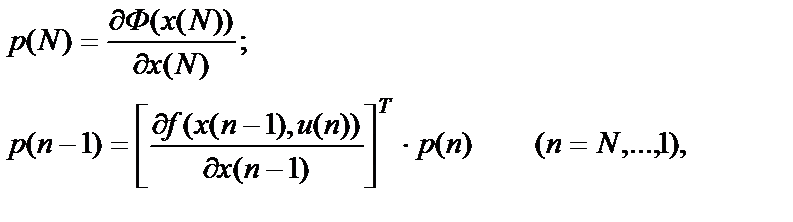(21)
где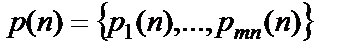 
,
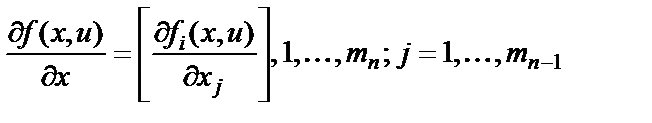; (22)
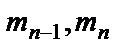– число нейронов соответственно в слое n –1 и в слое n; Т – знак операции транспонирования.
Сопряженная система описывает процесс, который в литературе принято называть «обратным распространением ошибки». Векторы p(n), n = 1, 2, …, N называются сопряженными, они являются коэффициентами чувствительности 
критерия качества процесса (21) к изменениям выходных сигналов x(n), n = 1, 2, …, N слоев нейронной сети. Каждому фиксированному процессу управления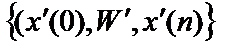 
соответствует своя сопряженная система (22) со своим набором переменных 
.
Система (22) является линейной системой с переменными параметрами. «Время» в сопряженной системе направлено в обратную сторону n = N,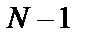 
, …, 1.
Определим функцию, которая носит название функции Гамильтона:
(23)
(n = 1, 2, …, N); (a,b) – скалярное произведение векторов a, b.
При фиксированных p и x функция Гамильтона становится функцией только управляющего воздействия W(n).
Обозначим через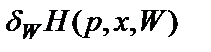 
допустимый дифференциал функции Гамильтона, т.е.
.
Если W* ={W*(1), W*(2),…,W*(N)} – оптимальные значения весовых коэффициентов для начального состояния 
в задаче (20), (21) , то имеют место следующие неравенства [5]:
|
|
|
; (24)
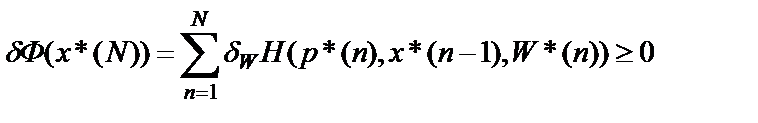. (25)
Неравенства являются необходимыми условиями оптимальности для задач дискретного управления вида (20), (21). Они показывают, что в оптимальной точке W* ={W*(1), W*(2),…,W*(N)} достигается минимум функционала (21).
Из неравенства (24) следует, что на оптимальном управлении выполняются необходимые условия минимума функции Гамильтона H(W(n)) на множестве W.
Формула (25) может быть переписана для произвольного управления W в следующем виде:
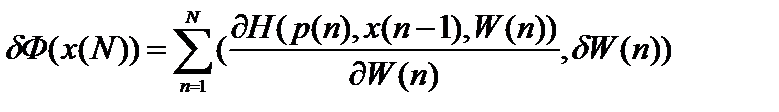. (26)
Она показывает в первом приближении изменение показателя качества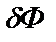 
в зависимости от изменения управления 
.
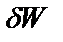Для подстройки весов многослойной нейронной сети можно использовать методы возможных направлений [5], которые состоят из следующих этапов:
· задание произвольных значений весовых коэффициентов для всех слоев;
· расчет по формулам (20), (21) сигналов x(n), n = 1, 2,…,N на выходе каждого слоя нейронов;
· расчет по формулам (22) сопряженного вектора p(n), n = N, N–1, …,1, по значению которого можно определить слой, наиболее влияющий на критерий оптимальности;
|
|
|
· вычисление для каждого слоя функции Гамильтона (23);
· для каждого слоя определение направления изменения значений весовых коэффициентов в сторону уменьшения функции Гамильтона одним из известных методов (градиентным, методом Ньютона и т.д.);
· определение длины шага и нового управления;
· оценка близости полученного решения к оптимальному решению.
К преимуществам рассмотренной модели можно отнести разбиение сложной задачи подстройки многослойной сети к подстройке коэффициентов каждого слоя. Получение значения сопряженного вектора (вектора чувствительности критерия к изменениям сигналов на выходе всех слоев сети) позволяет оценить те слои нейронной сети, которые наиболее сильно влияют на ошибку воспроизведения заданного выходного сигнала.
Эффективность использования многослойных нейронных систем устанавливается рядом так называемых теорем о полноте [1, 2]. Смысл данных теорем сводится к тому, что любая непрерывная функция на замкнутом ограниченном множестве может быть приближена функциями, вычисленными нейронными сетями. Таким образом, нейронные сети являются универсальными аппроксиматорами.
Дата добавления: 2019-11-16; просмотров: 225; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!