Сложение в восьмеричной системе

⇐ ПредыдущаяСтр 14 из 27Следующая ⇒

Сложение в шестнадцатиричной системе

При сложении цифры суммируются по разрядам, и если при этом возникает избыток, то он переносится влево.

Пример. Сложим числа 15 и 6 в различных системах счисления.

Шестнадцатеричная: F₁₆+6₁₆

Ответ: 15+6 = 21₁₀ = 10101₂ = 25₈ = 15₁₆.

Проверка. Преобразуем полученные суммы к десятичному виду:
10101₂ = 2⁴ + 2² + 2⁰ = 16+4+1=21,

25₈ = 2^.8¹ + 5^.8⁰ = 16 + 5 = 21,

15₁₆ = 1^.16₁ + 5^.16₀ = 16+5 = 21.

Пример. Сложим числа 15, 7 и 3.

Шестнадцатеричная: F₁₆+7₁₆+3₁₆

Ответ: 5+7+3 = 25₁₀ = 11001₂ = 31₈ = 19₁₆.
Проверка:
11001₂ = 2⁴ + 2³ + 2⁰ = 16+8+1=25,
31₈ = 3^.8¹ + 1^.8⁰ = 24 + 1 = 25,
19₁₆ = 1^.16¹ + 9^.16⁰ = 16+9 = 25.

Пример. Сложим числа 141,5 и 59,75.

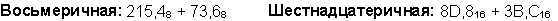
Ответ: 141,5 + 59,75 = 201,25₁₀ = 11001001,01₂ = 311,2₈ = C9,4₁₆
Проверка. Преобразуем полученные суммы к десятичному виду:
11001001,01₂ = 2⁷ + 2⁶ + 2³ + 2⁰ + 2^-2 = 201,25
311,2₈ = 3^.8² + 1^.8¹ + 1^.8⁰ + 2^.8^-1 = 201,25
C9,4₁₆ = 12^.16¹ + 9^.16⁰ + 4^.16^-1 = 201,25

Вычитание

Пример. Вычтем единицу из чисел 10₂, 10₈ и 10₁₆

Пример. Вычтем единицу из чисел 100₂, 100₈ и 100₁₆

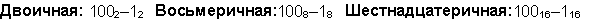
Пример. Вычтем число 59,75 из числа 201,25.

Ответ: 201,25₁₀ - 59,75₁₀ = 141,5₁₀ = 10001101,1₂ = 215,4₈ = 8D,8₁₆.
Проверка. Преобразуем полученные разности к десятичному виду:
10001101,1₂ = 2⁷ + 2³ + 2² + 2⁰ + 2^-1 = 141,5;
215,4₈ = 2^.8² + 1^.8¹ + 5^.8⁰ + 4^.8^-1 = 141,5;
8D,8₁₆ = 8^.16¹ + D^.16⁰ + 8^.16^-1 = 141,5.

Умножение

Выполняя умножение многозначных чисел в различных позиционных системах счисления, можно использовать обычный алгоритм перемножения чисел в столбик, но при этом результаты перемножения и сложения однозначных чисел необходимо заимствовать из соответствующих рассматриваемой системе таблиц умножения и сложения.

Умножение в двоичной системе

Умножение в восьмеричной системе

Ввиду чрезвычайной простоты таблицы умножения в двоичной системе, умножение сводится лишь к сдвигам множимого и сложениям.

Пример. Перемножим числа 5 и 6.

Ответ: 5^.6 = 30₁₀ = 11110₂ = 36₈.

Проверка. Преобразуем полученные произведения к десятичному виду:

11110₂ = 2⁴ + 2³ + 2² + 2¹ = 30;

36₈ = 3^.8¹ + 6^.8⁰ = 30.

Пример. Перемножим числа 115 и 51.

Ответ: 115^.51 = 5865₁₀ = 1011011101001₂ = 13351₈.

Проверка. Преобразуем полученные произведения к десятичному виду:
1011011101001₂ = 2¹² + 2¹⁰ + 2⁹ + 2⁷ + 2⁶ + 2⁵ + 2³ + 2⁰ = 5865;

13351₈ = 1^.8⁴ + 3^.8³ + 3^.8² + 5^.8¹ + 1^.8⁰ = 5865.

Деление

Деление в любой позиционной системе счисления производится по тем же правилам, как и деление углом в десятичной системе. В двоичной системе деление выполняется особенно просто, ведь очередная цифра частного может быть только нулем или единицей.

Пример. Разделим число 30 на число 6.

Ответ: 30 : 6 = 5₁₀ = 101₂ = 5₈.

Пример. Разделим число 5865 на число 115.

Восьмеричная: 13351₈ :163₈

Ответ: 5865 : 115 = 51₁₀ = 110011₂ = 63₈.
Проверка. Преобразуем полученные частные к десятичному виду:
110011₂ = 2⁵ + 2⁴ + 2¹ + 2⁰ = 51; 63₈ = 6^.8¹ + 3^.8⁰ = 51.

Пример. Разделим число 35 на число 14.

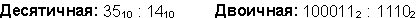
Восьмеричная: 43₈ : 16₈

Ответ: 35 : 14 = 2,5₁₀ = 10,1₂ = 2,4₈.
Проверка. Преобразуем полученные частные к десятичному виду:
10,1₂ = 2¹ + 2 ^-1 = 2,5;
2,4₈ = 2^.8⁰ + 4^.8^-1 = 2,5.

Формы представления чисел

В вычислительных машинах применяются две формы представления двоичных чисел – естественная форма или форма с фиксированной запятой (точкой) и нормальная форма или форма с плавающей запятой (точкой).

В естественной форме положение в разрядной сетке (общее число разрядов, отведенное для представления чисел, с указанием местоположения каждого из них) запятой, отделяющей целую часть числа от дробной части, постоянно для всех чисел. Диапазон значащих чисел небольшой и при m-разрядной целой части и s-разрядной дробной части числа без учета знака составляет от P^-s до P^m - P^-s. Кроме того, если в результате операции получится число, выходящее за допустимый диапазон, происходит переполнение разрядной сетки, и дальнейшие вычисления теряют смысл. Следовательно, необходимо прогнозировать результаты обработки с целью соответствующего масштабирования исходных данных. По этим причинам естественная форма представления используется как вспомогательная и только для целых чисел.

В нормальной форме каждое число представляется как N = ±MP^±^R, где М – мантисса числа (|M|<1), R – порядок (целое число), Р – основание системы счисления. Абсолютное значение порядка определяет число разрядов, на которое смещена запятая, отделяющая целую часть числа от дробной части, а знак порядка – направление смещения этой запятой. Таким образом, с изменением значения порядка запятая меняет своё положение, как бы "плавает" в изображении числа. Диапазон значащих чисел весьма велик и при m-разрядной мантиссе и s-разрядном порядке (без учета знаков порядка и мантиссы) составляет от до . В связи с этим нормальная форма представления является основной в современных ЭВМ.

Пример .

Приведем несколько равенств: левая часть равенства – число в естественной форме, правая часть – в нормальной форме. Для записи естественной формы используются 5 разрядов в целой части и 5 разрядов в дробной части.

+00721,35500 = +0,721355∙10³;

+00000,00328 = +0,328∙10^-2;

-10301,20260 = -0,103012026∙10⁵.

В соответствии с двоичным представлением в информатике введены специальные единицы измерения объемов информации, хранимой или обрабатываемой в ЭВМ (таблица 14).

Последовательность нескольких битов или байтов часто называют полем данных. В ПК могут обрабатываться поля постоянной и переменной длины.

Таблица 14

Единицы измерения объемов данных

Кол.двоич. разрядов	1	8	16	8∙1024 (8∙2¹⁰)	8∙1024² (8∙2²⁰)	8∙1024³ (8∙2³⁰)	8∙1024⁴ (8∙2⁴⁰)
Ед. измерения	Бит	Байт	Параграф	Килобайт (Кбайт)	Мегабайт (Мбайт)	Гигабайт (Гбайт)	Терабайт (Тбайт)

Поля постоянной длины могут быть следующих размеров (форматов): слово (4 байта), полуслово (2 байта), полуторное слово (6 байт), двойное слово (8 байт), расширенное слово (10 байт). В полях постоянной длины числа с фиксированной запятой чаще всего имеют формат слова (таблица 15а) и полуслова и заполняют формат справа налево. Оставшиеся свободными старшие разряды формата заполняются нулями. В крайнем левом разряде формата отображается знак числа, при этом знак "+" кодируется нулем, а знак "-" – единицей. Числа с плавающей запятой чаще всего имеют формат двойного (таблица 16б) и расширенного слова. Порядок заполняет соответствующую часть формата справа налево, а мантисса – слева направо. Оставшиеся свободными младшие разряды мантиссы формата заполняются нулями.

Таблица 15а

Структура формата слово со знаком для чисел с фиксированной (а)

a)№ разряда	Знак	Абсолютная величина числа
a)№ разряда	31	30	29	. . .	1	0

Таблица 16б

Структура формата слово со знаком для чисел с плавающей (б) запятой

б) № разряда	Порядок				Мантисса
	Знак	Абс. величина			Знак	Абс. величина
	63	62	. . .	56	55	54	. . .	0

При выполнении операций ввода-вывода данные часто представляются в двоично-десятичной системе счисления – когда каждая цифра десятичного числа отображается 4-разрядным двоичным числом. Двоично-десятичные числа представляются полями переменной длины в так называемых упакованном и распакованном форматах. В упакованном формате для каждой десятичной цифры отводится 4 двоичных разряда, при этом знак числа кодируется в крайнем правом полубайте (1100 – знак "+" и 1101 – знак "-"). Упакованный формат используется обычно в ПК при выполнении арифметических операций над двоично-десятичными числами. В распакованном формате для каждой десятичной цифры отводится байт, представляющий собой (кроме младшего байта) адрес соответствующей ячейки таблицы символов. В старшем полубайте адреса кодируется номер столбца, а в младшем – номер строки этой таблицы. Старший полубайт младшего (правого) байта используется для кодирования знака. Распакованный формат используется в ПК при вводе-выводе информации. Поля переменной длины могут иметь любой размер от 0 до 256 байт, но обязательно равный целому числу байтов.

Вещественные числа в компьютерах различных типов записываются по-разному, тем не менее, все компьютеры поддерживают несколько международных стандартных форматов, различающихся по точности, но имеющих одинаковую структуру следующего вида (рис. 17).

Рисунок 17. Структура точности различных типов

Здесь порядок n-разрядного нормализованного числа задается в так называемой смещенной форме: если для задания порядка выделено k разрядов, то к истинному значению порядка, представленного в дополнительном коде, прибавляют смещение, равное (2^k-1 - 1). Например, порядок, принимающий значения в диапазоне от -128 до +127, представляется смещенным порядком, значения которого меняются от 0 до 255.

Использование смещенной формы позволяет выполнять операции над порядками, как над беззнаковыми числами, что упрощает операции сравнения, сложения и вычитания порядков, а также упрощает операцию сравнения самих нормализованных чисел.

Чем больше разрядов отводится под запись мантиссы, тем выше точность представления числа. Чем больше разрядов занимает порядок, тем шире диапазон от наименьшего отличного от нуля числа до наибольшего числа, представимого в машине при заданном формате.

Дата добавления: 2019-09-13; просмотров: 705; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 9 10 11 12 131415 16 17 18 Следующая ⇒

Мы поможем в написании ваших работ!