Формирование целых чисел в позиционных системах счисления
В каждой системе счисления цифры упорядочены в соответствии с их значениями: 1 больше 0, 2 больше 1 и т.д.
Продвижением цифры называют замену её следующей по величине.
В десятичной системе, продвинуть цифру 1 значит заменить её на 2, продвинуть цифру 2 значит заменить её на 3 и т.д. Продвижение старшей цифры (например, цифры 9 в десятичной системе) означает замену её на 0. В двоичной системе, использующей только две цифры - 0 и 1, продвижение 0 означает замену его на 1, а продвижение 1 - замену её на 0.
Целые числа в любой системе счисления порождаются с помощью Правила счета [4]:
Для образования целого числа, следующего за любым данным целым числом, нужно
- продвинуть самую правую цифру числа;
- если какая-либо цифра после продвижения стала нулем, то нужно продвинуть цифру, стоящую слева от неё.
Применяя это правило, запишем первые десять целых чисел в известных системах счисления:
1. в двоичной системе: 0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001;
2. в троичной системе: 0, 1, 2, 10, 11, 12, 20, 21, 22, 100;
3. в пятеричной системе: 0, 1, 2, 3, 4, 10, 11, 12, 13, 14;
4. восьмеричной системе: 0, 1, 2, 3, 4, 5, 6, 7, 10, 11.
Принципы кодирования чисел в позиционных системах счисления
Чтобы перевести число, скажем, 12345N, из системы счисления с основанием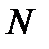 
в десятичную систему, нужно умножить значение каждой цифры на 
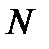в степени, равной ее разряду:
| N0 = 1 |
1 2 3 4 5N = 1·N4 + 2·N3 + 3·N2 + 4·N1 + 5·N0
1. последняя цифра записи числа в системе счисления с основанием – это остаток от деления этого числа на ;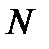
|
|
|
2. две последние цифры – это остаток от деления на 
, и т.д.
Пример. Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 25, запись которых в системе счисления с основанием четыре оканчивается на 11?
Общий подход: вспомним алгоритм перевода числа из десятичной системы в систему с основанием N, из него следует, что младшая цифра результата – это остаток от деления исходного числа на N, а две младших цифры – это остаток от деления на N 2 и т.д. В данном случае N =4, остаток от деления числа на N 2=16 должен быть равен 114 = 5. Потому задача сводится к тому, чтобы определить все числа, которые меньше или равны 25 и дают остаток 5 при делении на 16.
Решение (через десятичную систему): Общий вид чисел, которые дают остаток 5 при делении на 16 можно представить формулой k·16+5, , где k – целое неотрицательное число (0, 1, 2, …). Среди всех этих чисел нужно выбрать меньшие или равные 25 («не превосходят 25»). Таких чисел всего два: 5 (при k=0) и 21 (при k=1). Таким образом, верный ответ – 5, 21
Пример. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 23 оканчивается на 2.
|
|
|
Общий подход: Здесь обратная задача – неизвестно основание системы счисления означим его через N. Так как последняя цифра числа – 2, основание должно быть больше 2, то есть N >2. Вспомним алгоритм перевода числа из десятичной системы в систему с основанием N, из него следует, что младшая цифра результата – это остаток от деления исходного числа на N.
Решение: Итак, нужно найти все целые числа N ≥3, такие, что остаток от деления 23 на N равен 2, или то же самое, 23=k · N+2 (*), где k – целое неотрицательное число (0, 1, 2, …). Сложность состоит в том, что и k, и N неизвестны, в данном случае, нужно «играть» на том, что мы имеем дело с натуральными числами. Из формулы (*) получаем k · N =21, так что задача сводится к тому, чтобы найти все делители числа 21, которые больше 2; в этой задаче есть только три таких делителя: N=3,7 и 21; таким образом, верный ответ – 3, 7, 21.
Пример. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 31оканчивается на 11.
Общий подход: Неизвестно основание системы счисления, обозначим через N . Пока будем считать, что запись числа 31 в системе с основанием N состоит из трех цифр, причем две младшие (11) нам даны, а одну (обозначим ее через k) нужно найти:
|
|
|
2 1 0 ← разряды
1. k 1 1N = k·N2 + N1 + N0 = k·N2 + N + 1
Можно показать, что при большем количестве разрядов эта формула также верна, то есть, число 31 можно представить, как 31=k·N2+N+1 при некотором целом k . Например, для числа с пятью разрядами получаем:
4 3 2 1 0 ← разряды
31 = k4 k3 k2 1 1N = k4·N4 + k3·N3 + k2·N2 + N1 + N0= k·N2 + N + 1
Для k=k4N2+k3N+k2 (из первых трех слагаемых вынесли общий множитель N2).
Решение. Итак, нужно найти все целые числа N≥2, такие, что 31=k · N 2+N+1 (**), где k – целое неотрицательное число (0, 1, 2, …). Как и в предыдущем случае и k, и N неизвестны. Поэтому здесь тоже нужно «играть» на том, что это натуральные числа.Изформулы (**) получаем (k · N+1) N =30. Так что задача сводится к тому, чтобы найти все делители N числа 30 и отобрать только те из них, для которых уравнение (**) разрешимо при целом k, то есть,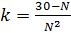 
– целое число выпишем все делители числа 30, большие или равные 2: 2, 3, 5, 6, 10, 15, 30. Из всех этих делителей только для 2, 3, 5 и 30 значение 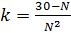– целое число (оно равно соответственно 7, 3, 1 и 0). Таким образом, верный ответ – 2, 3, 5, 30.
Пример. Укажите наименьшее основание системы счисления, в которой запись числа 30 трехзначна.
Решение. 1. Обозначим через N неизвестное основание системы счисления, тогда запись числа 30 в этой системе имеет вид x y zN = 30, вспомним алгоритм перевода числа из системы счисления с основанием 
в десятичную систему: расставляем сверху номера разрядов и умножаем каждую цифру на основание в степени, равной разряду:
|
|
|
Поскольку запись трехзначная, x≠0, поэтому 30≥N2. С другой стороны, четвертой цифры нет, то есть, в третьем разряде – ноль, поэтому 30<N3. Объединяя последние два условия, получаем, что искомое основание N удовлетворяет двойному неравенству N2£30<N3.
Учитывая, что N – целое число, методом подбора находим целые решения этого неравенства; их два – 4 и 5:
42=16£30<43=64;
52=25£30<53=125.
Минимальное из этих значений – 4. Таким образом, верный ответ – 4.
Решение (без подбора):
Найдем первое целое число, куб которого больше 30; это 4, так как
33=27<30<43=64.
Проверяем второе неравенство: 42=16£30, поэтому в системе счисления с основанием 4 запись числа 30 трехзначна. Таким образом, верный ответ – 4.
Пример. Покажите через запятую в порядке возрастания все десятичные числа, не превосходящие 30, запись которых в системе счисления с основанием 5 начинается на 3?
Решение. Нас интересуют числа от 1 до 29. Сначала определим, сколько цифр может быть в этих числах, записанных в системе счисления с основанием 5. Поскольку 52<29<53, в интересующих нас числах может быть от 1 до 3 цифр. Рассмотрим трехзначные числа, начинающиеся на 3 в системе с основанием 5: 3xy5=3·52+x·5+y , все они заведомо не меньше 3·52=75>29, поэтому в наш диапазон не попадают; Таким образом, остается рассмотреть только однозначные и двухзначные числа. Есть всего одно однозначное число, начинающееся на 3, это 3. Общий вид всех двузначных чисел, начинающихся на 3 в системе с основанием 5:
3·5+k=15+k , где k – целое число из множества {0, 1, 2,3,4} (поскольку система счисления имеет основание 5 и цифр, больших 4, в записи числа быть не может).
Используя эту формулу, находим интересующие нас двузначные числа – 15, 16, 17, 18 и 19. Таким образом, верный ответ – 3, 15, 16, 17, 18, 19.
Пример. Значение арифметического выражения: 98 + 35 – 9 записали в системе счисления с основанием 3. Сколько цифр «2» содержится в этой записи?
Решение. приведём все слагаемые к виду 3N и расставим в порядке убывания степеней: 98 + 35 – 9 = 316 + 35 – 32, первое слагаемое, 316, даёт в троичной записи одну единицу – она нас не интересует, пара 35 – 32 даёт 5 – 2 = 3 двойки. Ответ: 3.
Пример. Сколько единиц в двоичной записи числа
42015 + 8405 – 2150 – 122.
Решение. Приведём все числа к степеням двойки, учитывая, что
122 = 128 – 4 – 2 = 27 – 22 – 21: 42015 + 8405 – 2150 – 122 =
(22)2015 + (23)405 – 2150 – 27 + 22 + 21 = 24030 + 21215 – 2150 – 27 + 22 + 21.
Вспомним, число 2N –2K при K < N записывается как N– K единиц и K нулей: 
, для того чтобы использовать это свойство, нам нужно представить заданное выражение в виде пар вида 2N –2K, причём в этой цепочке степени двойки нужно выстроить по убыванию.
В нашем случае выражении 24030 + 21215 – 2150 – 27 + 22 + 21стоит два знака «минус» подряд, это не позволяет сразу использовать формулу, используем теперь равенство, так что – 2150 = – 2151 + 2150; получаем 24030 + 21215 – 2151 + 2150 – 27 + 22 + 21 здесь две пары 2N –2K, а остальные слагаемые дают по одной единице общее число единиц равно 1 + (1215 – 151) + (150 – 7) + 1 + 1 = 1210. ответ: 1210.
Дата добавления: 2019-09-13; просмотров: 355; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!