Теория проспектов и парадокс Алле
Применим теорию проспектов для анализа парадокса Алле (см. рис.2.6). Из левой лотереи следует
U > 1 Ä П(0,1) + U Ä П(0,89)
или

Из правой лотереи следует
П(0,1) > U Ä П(0,11)
или
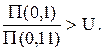
Нетрудно убедиться, что из перечисленных выше пяти свойств функции П(р) вытекает возможность выполнения неравенств

так как 1-П(0,89) > П(0,11) и 1 > П(0,11)+П(0,89). Следовательно, теория проспектов позволяет избежать парадокса Алле.
Новые парадоксы
Означает ли это, что теория проспектов дает возможность разрешить все противоречия между нормативной теорией, предписывающей нормы рационального поведения, и особенностями реального поведения людей? К сожалению, нет. Недостаточно формальный характер описанной выше процедуры редактирования проспекта допускает неоднозначное толкование и применение противоречивых эвристик. Приведем следующий пример [14].
Пусть необходимо сделать выбор между двумя лотереями:
Т=[($100; 0,5); ($51; 0,25)] и W=[($101; 0,5); ($50; 0,3)].
Если мы округлим $101 до $100, то первые части лотереи идентичны, и остается выбор между оставшимися частями. Здесь более естественным представляется округление вероятности до 0,3, и тогда лотерея Т является более предпочтительной ($51 против $50). Если же мы начнем со второй части лотерей, причем округлим как вероятность, так и полезность, то W становится более предпочтительной.
Найдено уже немало примеров, в которых процедуры редактирования проспектов приводят к противоречиям. Несмотря на это, теория проспектов является интересной аксиоматической теорией, стремящейся объединить дескриптивное знание о поведении людей и нормативные правила их рационального поведения.
|
|
|
Выводы по второй лекции
1. Задача принятия решений является одной из центральных в экономике. Предполагается, что лицо, принимающее решение, является рациональным человеком и его решения есть результат упорядоченного процесса мышления. На основе аксиом рациональности доказывается теорема о существовании функции полезности. Осуществляя выбор, рациональный человек максимизирует свою функцию полезности.
2. Наиболее простыми задачами принятия решений являются задачи с вазами. Выбор оптимального решения во многих задачах осуществляется с помощью деревьев решений. Дерево решений представляет все возможные варианты действий ЛПР. Для нахождения оптимального варианта используется метод «сворачивания» дерева.
3. Психологи и экономисты обнаружили ряд парадоксов, демонстрирующих, что поведение людей отличается от рационального. Были найдены многочисленные эвристики, используемые людьми при принятии решений. Нерациональность человека является общепризнанным фактом, который должен учитываться при анализе решений.
|
|
|
4. Теория проспектов построена с целью разрешения противоречий между наблюдаемым поведением ЛПР и требованиями рациональности. Теория проспектов учитывает многие поведенческие эффекты и позволяет устранить ряд парадоксов, возникающих при применении теории полезности.
Лекция 3
Дата добавления: 2019-09-13; просмотров: 222; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
