Тема 1.13. Движение материальной точки.

Метод кинетостатики

Иметь представление о свободных и несвободных материальных точках, о силах инерции, об использовании силы инерции для решения технических задач.

Знать формулы для расчета силы инерции при поступательном и вращательном движениях, знать принцип Даламбера и уметь определять параметры движения с использованием законов динамики и метода кинетостатики.

Свободная и несвободная точки

Материальная точка, движение которой в пространстве не ограничено какими-нибудь связями, называется свободной. Задачи решаются с помощью основного закона динамики.

Материальные точки, движение которых ограничено связями, называются несвободными.

Для несвободных точек необходимо определять реакции связей. Эти точки движутся под действием активных сил и ограничивающих движение реакций связей (пассивных сил).

Несвободные материальные точки освобождаются от связей: связи заменяются их реакциями. Далее несвободные точки можно рассматривать как свободные (принцип освобождаемое от связей).

Сила инерции

Инертность — способность сохранять свое состояние неизменным, это внутреннее свойство всех материальных тел.

Сила инерции — сила, возникающая при разгоне или торможении тела (материальной точки) и направленная в обратную сторону от ускорения. Силу инерции можно измерить, она приложена к «связям» — телам, связанным с разгоняющимся или тормозящимся телом.

Рассчитано, что сила инерции равна Fин =‌ ‌‌/‌ma/.

Тема 1.13. Движение материальной точки 101

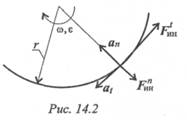
Таким образом, силы, действующие на материальные точки m1 и m2 (рис. 14.1), при разгоне платформы соответственно равны

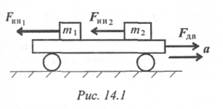
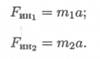Разгоняющееся тело (платформа с массой т (рис. 14.1)) силу инерции не воспринимает, иначе разгон платформы вообще был бы невозможен. При вращательном движении (криволинейном) возникающее ускорение принято представлять в виде двух составляющих: нормального а_п и касательного a t (рис. 14.2).

Поэтому при рассмотрении криволинейного движения могут возникнуть две составляющие силы инерции: нормальная и касательная

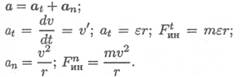
При равномерном движении по дуге всегда возникает нормальное ускорение, касательное ускорение равно нулю, поэтому действует только нормальная составляющая силы инерции, направленная по радиусу из центра дуги (рис. 14.3).

ω = const

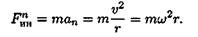
Принцип кинетостатики (принцип Даламбера)

Принцип кинетостатики используют для упрощения решения ряда технических задач. Реально силы инерции приложены к телам, связанным с разгоняющимся телом (к связям).

102 Лекция 14

Даламбер предложил условно прикладывать силу инерции к активно разгоняющемуся телу. Тогда система сил, приложенных к материальной точке, становится уравновешенной, и можно при решении задач динамики использовать уравнения статики.

Принцип Даламбера:

Материальная точка под действием активных сил, реакций связей и условно приложенной силы инерции находится в равновесии:

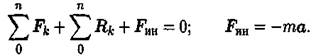
Порядок решения задач с использованием принципа Даламбера

1. Составить расчетную схему.

2. Выбрать систему координат.

3. Выяснить направление и величину ускорения.

4. Условно приложить силу инерции.

5. Составить систему уравнений равновесия.

6. Определить неизвестные величины.

Примеры решений задач

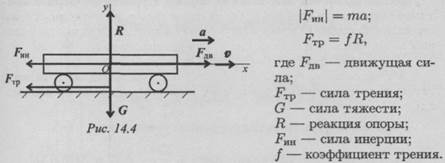
Пример 1. Рассмотрим движение платформы по шероховатой поверхности с ускорением (рис. 14.4).

Решение

Активные силы: движущая сила, сила трения, сила тяжести. Реакция в опоре R. Прикладываем силу инерции в обратную от ускорения сторону. По принципу Даламбера, система сил, действующих на платформу, становится уравновешенной, и можно составить уравнения равновесия. Наносим систему координат и составляем уравнения проекций сил.

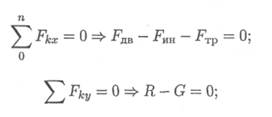
Тема 1.13. Движение материальной точки 103

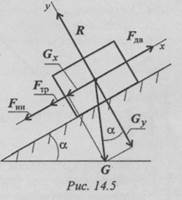
Пример 2. Тело весом 3500 Н движется вверх по наклонной плоскости согласно уравнению S = 0,16t² (рис. 14.5). Определить величину движущей силы, если коэффициент трения тела о плоскость f = 0,15.

Решение

1. Составим расчетную схему, выберем систему координат с осью
Ох вдоль наклонной плоскости.

Активные силы: движущая, сила трения, сила тяжести. Наносим реакцию в опоре перпендикулярно плоскости. Чтобы верно направить силу инерции, необходимо знать направление ускорения, определить это можно по уравнению движения.

При а > 0 движение равноускоренное.

2.Определяем ускорение движения: а = v ' = S "; v = S ' = 0,32t; а = v ' = 0,32 м/с² > 0.

Силу F_ин направим в обратную от ускорения сторону.

3.По принципу Даламбера составим уравнения равновесия:

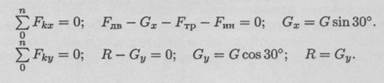
104 Лекция 14

4. Подставим все известные величины в уравнения равновесия:

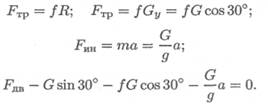
Выразим неизвестную силу и решим уравнение:

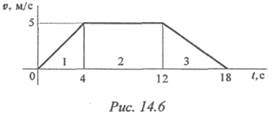
Пример 3. График изменения скорости лифта при подъеме известен (рис. 14.6). Масса лифта с грузом 2800 кг. Определить натяжение каната, на котором подвешен лифт на всех участках подъема.

Решение

1. Рассмотрим участок 1 — подъем с ускорением.

Составим схему cил (рис. 14.7). Уравнение равновесия кабины лифта:

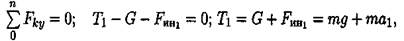
где Т — натяжение каната; G — сила тяжести; Fин — сила инерции, растягивающая канат.

Для определения ускорения на участке 1 учтем, что движение на этом участке равнопеременное, скорость v = v0 + at ; v0= 0. Следовательно, ускорение:

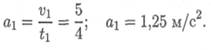
Тема 1.13. Движение материальной точки 105

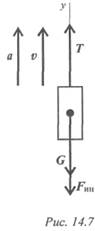
Определяем усилие натяжения каната при подъеме с ускорением 2800(9,81 + 1,25) = 30 968 Н; Т 1 = 30,97 кН.

2. Рассмотрим участок 2 — равномерный подъем.

Ускорение и сила инерции равны нулю. Натяжение каната равно силе тяжести.

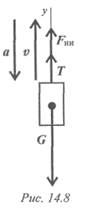
3. Участок 3 — подъем с замедлением.

Ускорение направлено в сторону, обратную направлению подъема. Составим схему сил (рис. 14.8).

Уравнение равновесия: Fин₃+ Тз — G = 0. Отсюда Тз = G — Fин₃= mg — ma3. Ускорение (замедление) на этом участке определяется с учетом того, что v = 0.

Таким образом, натяжение каната меняется при каждом подъеме и опускании, канат выходит из строя в результате усталости материала. Работоспособность зависит от времени.

Пример 4. Самолет выполняет «мертвую петлю» при скорости 160 м/с², радиус петли 1000 м, масса летчика 75 кг. Определить величину давления тела на кресло в верхней точке «мертвой петли».

106 Лекция 14

Решение

1. Схема сил, действующих на летчика (рис. 14.9):

Дата добавления: 2019-09-13; просмотров: 466; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 13 14 15 16 171819 20 21 22 Следующая ⇒

Мы поможем в написании ваших работ!