Метод минимальных путей и минимальных сечений
Минимальный путь − такой набор элементов в структуре, при котором система исправна, если исправны все элементы этого набора, отказ любого из элементов ведёт к отказу системы.
Минимальное сечение − такой набор элементов в структуре, при котором система неисправен, если неисправны все элементы этого набора, исключение любого элемент из набора переводит систему в исправное состояние.
У системы с произвольной структурой может быть несколько минимальных путей и минимальных сечений. Последовательное соединение из n элементов имеет один минимальный путь и n минимальных сечений, проходящих через каждый элемент. Параллельное соединение из n элементов имеет n минимальных путей, проходящих через каждый элемент, и одно минимальное сечение.
Пусть  множество всех минимальных путей. Событие состоящее в том, что все элементы
множество всех минимальных путей. Событие состоящее в том, что все элементы  исправны. Можно показать, что объединение событий
исправны. Можно показать, что объединение событий  совпадает с множеством всех отказовых состояний системы
совпадает с множеством всех отказовых состояний системы  , и поэтому для вероятности безотказной работы справедливо равенство:
, и поэтому для вероятности безотказной работы справедливо равенство:
 (5.1)
(5.1)
Пусть  множество всех минимальных сечений. Событие, состоящее в том, что все элементы сечения
множество всех минимальных сечений. Событие, состоящее в том, что все элементы сечения  неисправимы, обозначим также через
неисправимы, обозначим также через  . Можно показать, что объединение событий
. Можно показать, что объединение событий  совпадает с множеством всех отказовых состояний системы
совпадает с множеством всех отказовых состояний системы  , и поэтому для вероятности отказа системы справедливо равенство:
, и поэтому для вероятности отказа системы справедливо равенство:
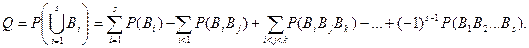 (5.2)
(5.2)
Пример 1.
Методом минимальных путей и минимальных сечений требуется рассчитать надёжность системы электроснабжения, структурная схема которой показана на рисунке 5.1 а).
Решение:
Найдём минимальные пути: 1− 3, 1− 4, 2 − 3, 2 − 4, по формуле (5.1):
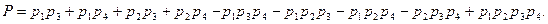
Найдём минимальные сечения 1 − 2, 3 − 4, По формуле (5.2):

 .
.
Верхняя оценка вероятности безотказной работы определяется как вероятность безотказной работы параллельного соединения минимальных путей. Верхняя оценка вероятности отказа системы определяется как вероятность отказа последовательного соединения минимальных сечений. Отсюда получаются двусторонние оценки вероятности безотказной работы:
 (5.3)
(5.3)
Пример 2.
Требуется оценить надёжность мостиковой схемы подстанции, структурная схема которой изображена на рисунке 5.2.
Решение.
Определим все минимальные пути соответствующие им вероятности:

Найдём все минимальные сечения и соответствующие им вероятности:

В соответствии с выражением (5.3) получим нижнюю и верхнюю оценки вероятности безотказной работы:

Если все элементы равнонадёжны, то оценки приобретают вид:

Логико-вероятностные методы анализа надёжности системы электроснабжения
Любой метод анализа надёжности требует описания условий работоспособности системы. Такие условия могут быть сфомулированы на основании:
− структурной схемы функционирования системы (схема расчёта надёжности);
− словесного описания функционирования системы;
− граф − схемы;
− функции алгебры логики.
Логико−вероятностный метод анализа надёжности позволяет дать определение и смысл благоприятных гипотез. Сущность этого метода заключается в следующем:
1. Состояние каждого элемента кодируется нулём и единицей:

В функции алгебры логики состояния элементов представляются в следующем виде:
−  исправное состояние элемента, соответствующее коду 1;
исправное состояние элемента, соответствующее коду 1;
−  отказовое состояние элемента, соответствующее коду 0.
отказовое состояние элемента, соответствующее коду 0.
2. Записывается с помощью функции алгебры логики условие работоспособности системы через работоспособность (состояние) её элементов. Полученная функция работоспособности системы является двоичной функцией двоичных аргументов.
3. Полученная функция алгебры логики преобразуется таким образом, чтобы в ней содержались члены, соответствующие благоприятным гипотезам исправной работы системы.
4. В функции алгебры логики вместо двоичных переменных  и
и  подставляются вероятности безотказной работы
подставляются вероятности безотказной работы  и вероятности отказа
и вероятности отказа  . Знаки конъюнкции и дизъюнкции заменяются алгебраическими умножением и сложением.
. Знаки конъюнкции и дизъюнкции заменяются алгебраическими умножением и сложением.
Полученное выражение и есть вероятность безотказной работы системы 
Пример 1.
Структурная схема системы электроснабжения представляет собой последовательное соединение элементов рисунок 5.3.

Рисунок 5.3 − Структурная схема системы электроснабжения с последовательным соединением 
На структурной схеме рисунок 5.3  состояние
состояние  го элемента системы, кодируемое 0, если элемент находится в отказовом состоянии, и 1, если он исправный. В данном случае система исправна, если исправны все элементы системы. Тогда функция алгебры логики является конъюнкцией логических переменных, т.е.
го элемента системы, кодируемое 0, если элемент находится в отказовом состоянии, и 1, если он исправный. В данном случае система исправна, если исправны все элементы системы. Тогда функция алгебры логики является конъюнкцией логических переменных, т.е.  представляющая собой совершенную дизъюнктивно нормальную форму системы.
представляющая собой совершенную дизъюнктивно нормальную форму системы.
Подставляя вместо логических переменных вероятности исправных состояний элементов и заменяя конъюнкцию на алгебраическое умножение, получим: 
Пример 2.
Структурная схема системы электроснабжения представляет собой дублированную систему с неравнонадёжными, постоянно включёнными подсистемами рисунок 5.4. На рисунке 5.4  и
и  состояния элементов системы. В таблице 5.1 представлена таблица истинности двух двоичных переменных. В таблице 0 − отказовое состояние элемента, 1− исправное состояние элемента. В данном случае система исправна, если исправны оба элемента (1,1) или один из них ((0,1) или (1,0)). Тогда работоспособное состояние системы описывается следующей функцией алгебры логики:
состояния элементов системы. В таблице 5.1 представлена таблица истинности двух двоичных переменных. В таблице 0 − отказовое состояние элемента, 1− исправное состояние элемента. В данном случае система исправна, если исправны оба элемента (1,1) или один из них ((0,1) или (1,0)). Тогда работоспособное состояние системы описывается следующей функцией алгебры логики:
 (5.1)
(5.1)

Рисунок 5.4 − Структурная схема дублированной системы электроснабжения
Таблица 5.1 − Таблица истинности двух двоичных переменных
| Х1 | Х2 | Y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Уравнение (5.1) является совершенной дизъюнктивной нормальной формой. Заменяя операции дизъюнкции и конъюнкции на алгебраические операции умножения и сложения, а логические переменные − на соответствующие вероятности состояния элементов, получим вероятность безотказной работы системы электроснабжения:

Пример 3.
Структурная схема электроснабжения имеет вид, показанный на рисунке 5.5.

Рисунок 5.5 − Структурная схема системы электроснабжения
Составим таблицу истинности таблица 5.2. В данном примере система исправна, если исправны все её элементы или исправным является элемент  и один из элементов дублированной пары
и один из элементов дублированной пары  На основании таблицы истинности совершенная дизъюнктивная нормальная форма (СДНФ) будет иметь вид:
На основании таблицы истинности совершенная дизъюнктивная нормальная форма (СДНФ) будет иметь вид: 
Таблица 5.2. Таблица истинности
| Х1 | Х2 | Х3 | Y |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Подставляя вместо двоичных переменных соответствующие вероятности, а вместо конъюнкций и дизъюнкций – алгебраические умножение и сложение, получим вероятность безотказной работы системы.

Функцию алгебры логики можно представить в минимальной форме, если воспользоваться следующими преобразованиями:
– вынос за скобки: 
– поглощение: 
– склеивание: 
Операции поглощения и склеивания в алгебре не применимы. В связи с этим нельзя полученную функцию алгебры логики (ФАЛ) минимизировать, а затем вместо логических переменных подставлять значения вероятностей. Вероятности состояний элементов следует подставлять в СДНФ, а упрощать по правилам алгебры.
Недостатком описанного метода является необходимость составления таблицы истинности, что требует перебора всех работоспособных состояний системы электроснабжения.
5.5 Метод кратчайших путей и минимальных сечений
Рассмотрим данный метод с позиции алгебры логики. Функцию работоспособности можно описать с помощью кратчайших путей успешного функционирования системы и минимальных сечений её отказа.
Кратчайшим путём называется минимальная конъюнкция работоспособных состояний элементов, образующих работоспособную систему.
Минимальным сечением называется минимальная конъюнкция неработоспособных состояний элементов, образующих неработоспособное состояние системы.
Пример 1.
Необходимо образовать функцию работоспособности системы, структурная схема которой представлена на рисунке 5.6, используя метод кратчайших путей и минимальных сечений.

Рисунок 5.6 – Структурная схема системы с неравнонадёжными элементами
Решение:
В данном случае кратчайшими путями, образующими работоспособную систему, будут:  Тогда функция работоспособности запишется в виде следующей функции алгебры логики:
Тогда функция работоспособности запишется в виде следующей функции алгебры логики:

В соответствии с этой ФАЛ структурная схема системы электроснабжения рисунок 5.6 может быть представлена структурной схемой рисунок 5.7. Минимальными сечениями, образующими неработоспособную систему, будут:  Тогда функция неработоспособности запишется в виде следующей функции алгебры логики:
Тогда функция неработоспособности запишется в виде следующей функции алгебры логики:

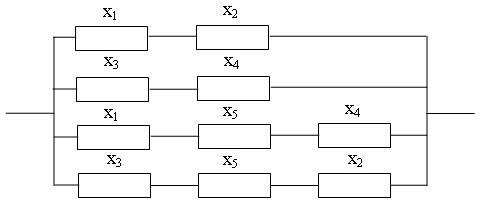
Рисунок 5.7 – Структурная схем а работоспособной системы, соответствующей ФАЛ.
На рисунке 5.8 представлена структурная схема неработоспособной системы электроснабжения.

Рисунок 5.8 – Структурная схема неработоспособного состояния системы
Следует иметь в виду, что структурные схемы рисунок 5.7 и рисунок 5.8 не являются схемами расчёта надёжности, а выражения для ФАЛ работоспособного и неработоспособного состояний не являются выражениями для определения вероятности безотказной работы и вероятности отказа:
 , (ФАЛ для кратчайших путей),
, (ФАЛ для кратчайших путей),
 ,(ФАЛ метода минимальных сечений).
,(ФАЛ метода минимальных сечений).
Основные достоинства ФАЛ в том, что они позволяют получить формально, не составляя таблицы истинности, СДНФ и СКНФ (совершенная конъюнктивная нормальная форма), которые дают возможность получить вероятность безотказной работы (вероятность отказа) системы путём подстановки в ФАЛ вместо логических переменных соответствующих значений вероятностей безотказной работы, заменив операции конъюнкции и дизъюнкции на алгебраические операции умножения и сложения. Для получения СДНФ необходимо каждый дизъюнктивный член ФАЛ умножить на  , где
, где  недостающий аргумент, и раскрыть скобки. Ответом будет СДНФ. Рассмотрим этот способ в следующем примере.
недостающий аргумент, и раскрыть скобки. Ответом будет СДНФ. Рассмотрим этот способ в следующем примере.
Пример 2.
Необходимо определить вероятность безотказной работы системы, структурная схема которой приведена на рисунке 5.6. Вероятности безотказной работы элементов равны 
Решение:
Воспользуемся методом кратчайших путей. Функция алгебры логики, полученная методом кратчайших путей, имеет вид:

Получим СДНФ системы. Для этого умножим дизъюнктивные члены на недостающие  :
:
 Раскрывая скобки и выполняя преобразования по правилам алгебры логики, получим СДНФ:
Раскрывая скобки и выполняя преобразования по правилам алгебры логики, получим СДНФ:
 Подставляя в СДНФ вместо
Подставляя в СДНФ вместо  вероятности безотказной работы
вероятности безотказной работы  и используя соотношение
и используя соотношение  , получим следующее выражение для вероятности безотказной работы системы электроснабжения
, получим следующее выражение для вероятности безотказной работы системы электроснабжения 
Из приведённого примера видно, что метод кратчайших путей освободил нас от определения благоприятных гипотез. Тот же результат можно получить, если воспользоваться методом минимальных сечений.
Тема 6. Исследование надёжности системы электроснабжения с использованием метода статистических испытаний (метод Монте − Карло)
Данный метод базируется на использовании значений случайных величин с заданным распределением вероятностей. Сущность метода статистического моделирования состоит в построении алгоритма, имитирующего поведение системы. В результате статистического моделирования системы получается серия частных значений искомых показателей надёжности. Эти значения обрабатываются и классифицируются методами математической статистики, что позволяет получить сведения о надёжности реальной системы в произвольные моменты времени. Если количество реализаций N достаточно велико, то результаты моделирования системы приобретают статистическую устойчивость и могут быть приняты в качестве оценок искомых показателей надёжности.
Теоретической основой метода являются предельные теоремы теории вероятностей. Принципиальное значение предельных теорем состоит в том, что они гарантируют высокое качество статистических оценок показателей надёжности при весьма большом числе испытаний (реализаций). Практически приемлемые количественные оценки показателей надёжности систем могут быть получены уже при сравнительно небольших значениях N.
Предположим, что требуется вычислить неизвестную величину m. Это может быть, например, математическое ожидание некоторой случайной величины  .Если N достаточно велико, то, согласно центральной предельно теореме, распределение величины
.Если N достаточно велико, то, согласно центральной предельно теореме, распределение величины  будет приблизительно нормальным с параметрами m и
будет приблизительно нормальным с параметрами m и  При этом имеет место приближённое равенство:
При этом имеет место приближённое равенство:
 ,
,
где:  функция Лапласа.
функция Лапласа.
Это чрезвычайно важное соотношение для метода Монте-Карло. Оно даёт нам и метод расчёта m, и оценку погрешности.
Пример 1.
Требуется определить долю времени  , в течение которого система находится в исправном состоянии при её функционировании в течение времени t. Здесь m(t) − средняя суммарная наработка. Функционирование системы представляет собой альтернирующий процесс с двумя состояниями: исправная работа и восстановление после возникновения отказа системы. Пусть f(x) − плотность распределения времени исправной работы, а g(x) − плотность распределения времени восстановления системы.
, в течение которого система находится в исправном состоянии при её функционировании в течение времени t. Здесь m(t) − средняя суммарная наработка. Функционирование системы представляет собой альтернирующий процесс с двумя состояниями: исправная работа и восстановление после возникновения отказа системы. Пусть f(x) − плотность распределения времени исправной работы, а g(x) − плотность распределения времени восстановления системы.
Решение:
Пусть случайные числа  , имеющих распределение вероятностей с плотностью f(x), и
, имеющих распределение вероятностей с плотностью f(x), и  , имеющих распределение вероятностей с плотностью g(x). Один из возможных вариантов расположения чисел
, имеющих распределение вероятностей с плотностью g(x). Один из возможных вариантов расположения чисел  и
и  показан на рисунке 6.1. Число проводимых опытов заранее неизвестно, оно определяется моментом времени t и значениями чисел
показан на рисунке 6.1. Число проводимых опытов заранее неизвестно, оно определяется моментом времени t и значениями чисел  и
и  .
.
Для решения задачи должно быть предусмотрено накопление двух сумм: суммарной наработки  , равной сумме
, равной сумме  и S, равной сумме
и S, равной сумме  и
и  .
.

Рисунок 6.1 − Диаграмма, иллюстрирующая определение функции 
Опишем алгоритм метода статистического моделирования:
1. 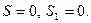
2. Пока  , выполнить:
, выполнить:
− рассмотрение  и
и  ;
;
− если 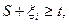 то
то  выйти из цикла;
выйти из цикла;
− иначе, если  то
то  выйти из цикла.
выйти из цикла.
3.  .
.
4. 
5.  .
.
В результате работы этого алгоритма будет получена одна из реализаций функции  Выполнив этот алгоритм многократно, получим множество реализаций, и тогда истинное значение требуемой величины можно принять среднее арифметическое этих реализаций.
Выполнив этот алгоритм многократно, получим множество реализаций, и тогда истинное значение требуемой величины можно принять среднее арифметическое этих реализаций.
Рассмотрим поведение функции  для следующих исходных данных: время безотказной работы имеет экспоненциальное распределение с параметром
для следующих исходных данных: время безотказной работы имеет экспоненциальное распределение с параметром  час−1, время восстановления также имеет экспоненциальное распределение с параметром
час−1, время восстановления также имеет экспоненциальное распределение с параметром  час−1.
час−1.
В таблице 6.1 получены значения функции  для N = 20 опытов (реализаций), для N = 500 опытов и точное значение, рассчитанное по формуле:
для N = 20 опытов (реализаций), для N = 500 опытов и точное значение, рассчитанное по формуле:

Соответствующая графическая иллюстрация приведена на рисунке 6.2 в виде трёх графиков. Из рисунка 6.2 следует вывод о существенной зависимости  от числа опытов. При малом числе опытов (N = 20) наблюдается значительное отклонение кривой
от числа опытов. При малом числе опытов (N = 20) наблюдается значительное отклонение кривой  от истинной. При большом числе опытов (N = 500) график функции
от истинной. При большом числе опытов (N = 500) график функции  оказывается очень близким к истинному.
оказывается очень близким к истинному.
Таблица 6.1 Значения доли времени пребывания системы в исправном состоянии
| t, час | N =20 | N = 500 | Точное |
| 0 | 1 | 1 | 1 |
| 100 | 0,974 | 0,976 | 0,981 |
| 200 | 0,975 | 0,98 | 0,979 |
| 300 | 0,987 | 0,978 | 0,978 |
| 400 | 0,962 | 0,98 | 0,977 |
| 500 | 0,97 | 0,975 | 0,977 |
| 600 | 0,978 | 0,975 | 0,977 |
| 700 | 0,958 | 0,974 | 0,976 |
| 800 | 0,971 | 0,976 | 0,976 |
| 900 | 0,984 | 0,977 | 0,976 |
| 1000 | 0,964 | 0,977 | 0,976 |

Рисунок 6.2 − Доля времени пребывания в исправном состоянии для N = 20 (кривая 1), для N = 500 (кривая 2), точное значение (кривая 3)
Дата добавления: 2019-09-13; просмотров: 1426; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
