Return (-1); //Аварийный выход: не хватает памяти

⇐ ПредыдущаяСтр 5 из 5

/ / **************** ОТЛАДКА ***********************

// n = 2; x0[0] = -1.2; x0[1] = 1.0;

// dx[0] = 0.8; dx[1] = 0.8;

//********** на функции Розенброка ***************

//**************** ОТЛАДКА ***********************

// n = 2; x0[0] = 0.5; x0[1] = 0.5;

// dx[0] = 0.8; dx[1] = 0.8;

//******** на функции Изона-Фентона *************

//----------------------------------------------

// Начальные присвоения

// ----------------------------------------------

n = np;

for(i = 0; i < n; i++) x0[i] = x[i];

err = Fx (n,x0,&f0,&jch); // Вычисление целевой функции

if (err < 0) goto ER0;

P0: err = poisk(n,dx,x0,&f0,x1,&f1,&jch); // Поиск из x0

if (err < 0) goto ER0;

// pr_Fx(n,x0,f0,jch," Функция Розенброка "); // ОТЛАДКА

if (f1 == f0) { // Поиск неудачен

for(i = 0; i < n; i++) dx[i] *= 0.5; // Уменьшаем шаг

nor_dx = 0.0; // Не мал ли шаг ?

for(i = 0; i < n; i++) nor_dx += dx[i] * dx[i];

nor_dx = sqrt(nor_dx);

if (nor_dx <= eps) goto VIX; // Выход по размеру шага

goto P0;

}

// Диагональный шаг или поиск по образцу

D0: for(i = 0; i < n; i++) x2[i] = 2.0 * x1[i] - x0[i];

err = Fx (n,x2,&f2,&jch); //Вычисление целевой функции

if (err < 0) goto ER0;

// pr_ Fx (n,x0,f0,jch,"Функция Розенброка"); // ОТЛАДКА

/* Удачен ли диагональный шаг ? */

err = poisk(n,dx,x2,&f2,x3,&f3,&jch); /* Поиск из т. X2

if (err < 0) goto ER0;

if (f3 >= f1) { // Диагональный шаг неудачен, ищем

Новое направление

for(i = 0; i < n; i++) x0[i] = x1[i];

f0 = f1;

goto P0;

} else { // Диагональный шаг удачен, шагнем еще...

for(i = 0; i < n; i++) {

x0[i] = x1[i]; x1[i] = x3[i];

}

f0 = f1; f1 = f3;

goto D0;

}

ER 0: //Здесь должно быть диагностическое сообщение

return (-1);

VIX : //Нормальный выход из программы

for(i = 0; i < n; i++) x[i] = x0[i];

*fmin = f0;

return (0);

}

//=========================================================

int poisk(int n, double *dx, double *xo, double *fo,

double *xn, double *fn, unsigned *ch)

{

/********************************************************/

// Исследующий поиск из точки XO,FO и поиск точки XN,FN

int j, flag, err;

double f1;

//------------------------------------------------------

for (j = 0; j < n; j++) xn[j] = xo[j];

*fn = *fo;

for(j = 0; j < n; j++) {

// Циклическое изменение переменных и анализ последствий...

xn[j] = xo[j] + dx[j];

flag = 0;

Z0: err = Fx (n,xn,&f1,ch); // Вычисление целевой функции if ( err < 0) return (-1);

if (f1 < *fn) { *fn = f1; goto NEXT; }

if (flag == 0) { flag = 1;

xn[j] = xo[j] - dx[j];

goto Z0;

}

xn[j] = xo[j];

NEXT: ;

}

return(0);

}

//=========================================================

int Fx(int n,double *x, double *f, unsigned *ch)

// Вычисление целевой функции

{

//------------- ОТЛАДКА на функции Розенброка ----- ----- ---

// *f = 100.0 * (x[1]-x[0]*x[0]) * (x[1]-x[0]*x[0]) +

// (1.0-x[0])*(1.0-x[0]);

//---------------------------------------------------------

//------------ ОТЛАДКА на функции Изона-Фентона -----------

// *f = (12.0 + x[0]*x[0] + (1.0+x[1]*x[1])/(x[0]*x[0]) + // (x[0]*x[0]*x[1]*x[1]+100.0)/

// (x[0]*x[0]*x[1]*x[1]*x[0]*x[0]*x[1]*x[1]))/10.0;

//---------------------------------------------------------

// Здесь должна быть Ваша целевая функция

//---------------------------------------------------------

*ch += 1U;

return(1);

}

//**** ОТЛАДОЧНАЯ ПЕЧАТЬ для тестовых функций *****

void pr_Fx(int n,double *x, double f, unsigned ch,

char * txt )

{ // Печать текущих параметров

FILE * Print ;

char t[64];

Print = fopen(“Debugging.txt”,”a+”);

fprintf(Print,”%s \n”,txt);

sprintf(Print," X[1] = %12g",x[0]);

sprintf(Print," X[2] = %12g",x[1]);

sprintf(Print," F = %12g",f);

sprintf(Print," Счетчик = %u \n",ch);

return; // ***** Конец ОТЛАДОЧНОЙ ПЕЧАТИ ****

}

Исследования программы на классических тестовых функциях, а именно, на функции Розенброка и функции Изона-Фентона [2] показали высокую скорость предложенной модификации метода. По данным [4, кн.1, стр.136-137] лучший метод достигает минимума функции Розенброка за 204, а функции Изона-Фентона за 92 вычисления целевой функции. Предложенный модифицированный алгоритм достиг экстремумов соответственно за 166 и 55 вычислений целевой функции.

4.2. Метод деформируемого многогранника.

Нелдер и Мид [2] предложили метод поиска, несколько более сложный по сравнению с прямым поиском Хука-Дживса, но оказавшийся весьма эффективным и легко осуществляемым на на компьютере. Чтобы читатель смог оценить стратегию Нелдера и Мида, кратко опишем симплексный поиск Спендли, Хекста и Химсворта [2], разработанный в связи со статистическим планированием эксперимента.

Вспомним, что регулярные многогранники в эвклидовом пространстве Е^п являются симплексами. Например, как видно из рис. 11, для случая двух переменных регулярный симплекс представляет собой равносторонний треугольник (три точки); в случае трёх переменных регулярный симплекс представляет собой тетраэдр (четыре точки) и т. д.

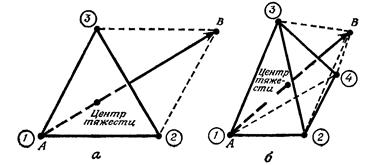
Рис. 11. Регулярные симплексы для двух (а) и трёх (б) переменных.

обозначает вершину с наибольшим значением целевой функции f ( X ); стрелка показывает направление наискорейшего уменьшения f ( X ).

При поиске минимума целевой функции f ( X ) пробные векторы X могут быть выбраны в точках пространства проектных переменных Eⁿ,находящихся в вершинах симплекса, как было первоначально предложено Спендли, Хекстом и Химсвортом. Из аналитической геометрии известно, что координаты вершин регулярного симплекса определяются следующей матрицей D, в которой столбцы представляют собой вершины, пронумерованные от 1 до (п + 1), а строчки - координаты; номер строки i принимает значения от 1 до п:

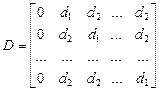- матрица n ´ (n+1),

где

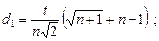
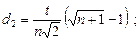
t - расстояние между двумя вершинами. Например, для п = 2 и t = 1 треугольник, приведённый на рис. 11(а), имеет следующие координаты вершин.

Таблица 1. Координаты вершин плоского симплекса

№ вершины ( i )	x₁ⁱ	x₂ⁱ
1	0	0
2	0.965	0.259
3	0.259	0.965

Целевая функция может быть вычислена в каждой из вершин симплекса; из вершины, где целевая функция максимальна (точка А на рис. 11), проводится проектирующая прямая через центр тяжести симплекса. Затем точка А исключается и строится новый симплекс, называемый отражённым, из оставшихся прежних точек и одной новой точки В, расположенной на проектирующей прямой на надлежащем расстоянии от центра тяжести. Продолжение этой процедуры, в которой каждый раз вычёркивается вершина, где целевая функция максимальна, а также использование правил уменьшения размера симплекса и предотвращения циклического движения в окрестности экстремума позволяют осуществить поиск, не использующий производные и в котором величина шага на любом этапе k фиксирована, а направление поиска можно изменять. На рис. 12 приведены последовательные симплексы, построенные в двумерном пространстве с «хорошей» целевой функцией.

Определённые практические трудности, встречающиеся при использовании регулярных симплексов, а именно отсутствие ускорения поиска и трудности при проведении поиска на искривлённых «оврагах» и «хребтах», привели к необходимости некоторых улучшений симплекс-метода. В этом разделе мы изложим метод Нелдера и Мида, в котором симплекс может изменять свою форму и, таким образом, уже не будет оставаться симплексом. Именно поэтому здесь использовано более подходящее название «деформируемый многогранник».

В методе Нелдера и Мида минимизируется функция п независимых переменных с использованием n +1 вершин деформируемого многогранника в пространстве проектных переменных Е^п.

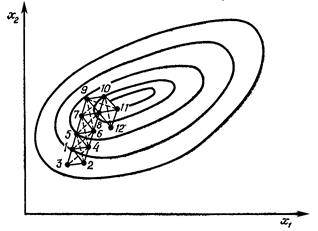
Рис. 12. Последовательность регулярных симплексов при минимизации функции f ( x ₁ , x ₂ ).

Каждая вершина многогранника может быть идентифицирована вектором X. Вершина (точка) в которой значение f ( X ) максимально, проектируется через центр тяжести многогранника. Улучшенные (более низкие) значения целевой функции находятся последовательной заменой точки с максимальным значением f ( X ) на более «хорошие» точки, пока не будет найден минимум f ( X ).

Более подробно этот алгоритм может быть описан следующим образом.

Пусть X_i ⁽ ^k ⁾ = { х _i ₁ ⁽ ^k ⁾... х _ij ⁽ ^k ⁾ , … х _in ⁽ ^k ⁾ }^T, i = 1 ... (п + 1), является i-той вершиной (точкой) в пространстве проектных переменныхна k -томэтапе поиска, k = 0, 1, ..., и пусть значение целевой функции в i-той вершине X_i ⁽ ^k ⁾ равно f(X_i ⁽ ^k ⁾ ). Кроме того, отметим те векторы X многогранника, которые дают максимальное и минимальное значения f ( X ). Определим

f(X_h ⁽ ^k ⁾ ) = max { f(X ₁ ⁽ ^k ⁾ ), f(X ₂ ⁽ ^k ⁾ )… f(X_n ₊₁ ⁽ ^k ⁾ ) },

где X_h^(k) = X_i^(k), и

f(X_l^(k)) = min { f(X₁^(k)), f(X₂^(k))… f(X_n+1^(k)) },

где X_l ⁽ ^k ⁾ = X_i ⁽ ^k ⁾ . Поскольку многогранник состоит из (п+1) вершин X ₁ ... X_n ₊₁ , то пусть X _п+2 будет центром тяжести всех вершин, с отсчётом от X_h.

Тогда координаты этого центра определяются формулой

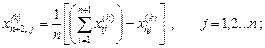(25)

где индекс j обозначает координатное направление.

Начальный многогранник обычно выбирается в виде регулярного симплекса (но это не обязательно) с точкой 1 в качестве начала координат; можно начало координат поместить в центре тяжести. Процедура отыскания точки в пространстве проектных переменных, в которой f ( X) имеет минимальное значение, состоит из следующих операций.

1. Отражение - проектирование X_h ⁽ ^k ⁾ через центр тяжести в соответствии с соотношением

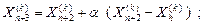(26)

где α > 0 является коэффициентом отражения; 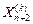- центр тяжести, вычисляемый по формуле (25); 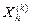- вершина, в которой функция f ( X ) принимает наибольшее из (п + 1) её значений на k -томэтапе.

2. Растяжение. Эта операция заключается в следующем: если

f(X_n ₊₃ ⁽ ^k ⁾ ) ≤ f(X_l ⁽ ^k ⁾ ), то вектор 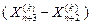растягивается в соответствии с соотношением

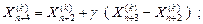(27)

где γ > 1 представляет собой коэффициент растяжения. Если f(X_n ₊₄ ⁽ ^k ⁾ ) < f(X_l ⁽ ^k ⁾ ), то X_h ⁽ ^k ⁾ заменяется на X_n ₊₄ ⁽ ^k ⁾ и процедура продолжается снова с операции 1 при k = k + 1. В противном случае X_h ⁽ ^k ⁾ заменяется на X_n ₊₃ ⁽ ^k ⁾ и также осуществляется переход к операции 1 при k = k + 1.

3. Сжатие. Если f(X_n ₊₃ ⁽ ^k ⁾ ) > f(X_i ⁽ ^k ⁾ ), для всех i ≠ h, то вектор 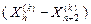сжимается в соответствии с формулой

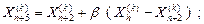(28)

где 0 < β < 1 представляет собой коэффициент сжатия. Затем X_h ⁽ ^k ⁾ заменяем на X_n ₊₅ ⁽ ^k ⁾ и возвращаемся к операции 1 для продолжения поиска на (k + 1)-м шаге.

4. Редукция. Если f(X_n ₊₃ ⁽ ^k ⁾ ) > f(X_h ⁽ ^k ⁾ ), то все векторы 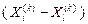, i = 1, 2 ...(n + 1); уменьшаются в 2 раза с отсчётом от X_l ⁽ ^k ⁾ в соответствии с формулой

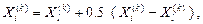i = 1, 2 ... (n + 1). (29)

Затем возвращаемся к операции 1 для продолжения поиска на (k + 1) шаге.

Критерий окончания поиска, использованный Нелдером и Мидом, состоял в проверке условия

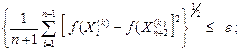(30)

где ε - произвольное малое число, а f(X_n ₊₂ ⁽ ^k ⁾ ) - значение целевой функции в центре тяжести многогранника X_n ₊₂ ⁽ ^k ⁾.

На рис. 13 приведена блок-схема поиска методом деформируемого многогранника, а на рис. 14 показана последовательность поиска для функции Розенброка,

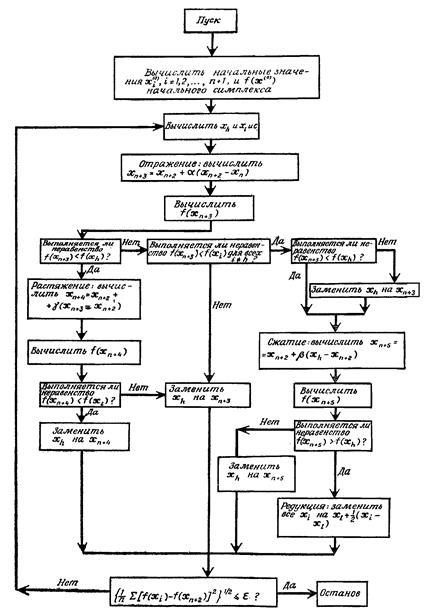
Рис. 13. Блок-схема метода Нелдера-Мида

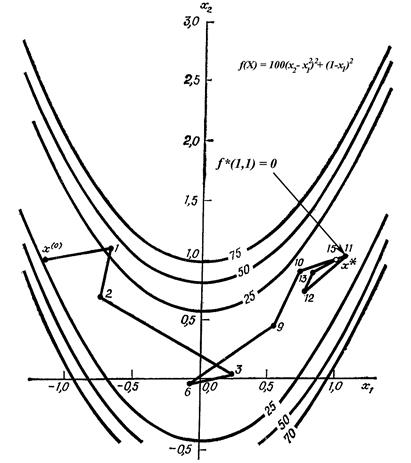
Рис. 14. Поиск минимума функции Розенброка

начиная из X⁽⁰⁾ ={-1.2 1.0}^T. Деформируемый многогранник в противоположность жёсткому симплексу адаптируется к топографии целевой функции, вытягиваясь вдоль длинных наклонных плоскостей, изменяя направление в изогнутых впадинах и сжимаясь в окрестности минимума. Коэффициент отражения ос используется для проектирования вершины с наибольшим значением f ( X ) через центр тяжести деформируемого многогранника. Коэффициент γ вводится для растяжения вектора поиска в случае, если отражение даёт вершину со значением f ( X ), меньшим, чем наименьшее значение f ( X ), полученное до отражения. Коэффициент сжатия β используется для уменьшения вектора поиска, если операция отражения не привела к вершине со значением f ( X ), меньшим, чем второе по величине (после наибольшего) значение f ( X ), полученное до отражения. Таким образом, с помощью операций растяжения или сжатия размеры и форма деформируемого многогранника масштабируются так, чтобы они удовлетворяли топологии решаемой задачи.

Естественно возникает вопрос, какие значения параметров α, β и γ должны быть выбраны. После того как форма и размер деформируемого многогранника подходящим образом выбран, его размеры должны поддерживаться неизменными, пока изменения в топологии задачи не потребуют применения многогранника другой формы. Это возможно реализовать только при α = 1. Кроме того, Нелдер и Мид показали, что при решении задачи с α = 1 требуется меньшее количество вычислений функции, чем при α < 1. С другой стороны, значение α не должно быть много больше единицы, поскольку 1) деформируемый многогранник легче адаптируется к топологии задачи при меньших значениях α, особенно когда необходимо изменять направление поиска, столкнувшись с изогнутой впадиной, и 2) в области локального минимума размеры многогранника должны уменьшаться и большое α в этих условиях замедлит сходимость. Таким образом, значение α = 1 выбирается как компромисс.

Чтобы выяснить, какое влияние на процедуру поиска имеет выбор β и γ, Нелдер и Мид, а также Павиани [2] провели решение нескольких тестовых задач, используя большое число различных комбинаций значений β и γ. В качестве удовлетворительных значений этих параметров при оптимизации без ограничений Нелдер и Мид рекомендовали α = 1; β = 0.5 и γ = 2.0. Размеры и ориентация исходного многогранника в некоторой степени влияли на время решения, а значения α, β и γ оказывали значительно большее влияние. Павиани отмечает, что нельзя чётко решить вопрос относительно выбора β и γ и что влияние выбора β на эффективность поиска несколько более заметно, чем влияние γ. Павиани рекомендует следующие диапазоны значений для этих параметров: 0.4 ≤ β ≤ 0.6; 2.8 ≤ γ ≤ 3.0. При 0 < β < 0.4 существует вероятность того, что из-за уплощения многогранника будет иметь место преждевременное окончание процесса. При β > 0.6 может потребоваться избыточное число шагов и больше машинного времени для достижения окончательного решения.

Пример 9. Поиск методом деформируемого многогранника. Для иллюстрации метода Нелдера и Мида рассмотрим задачу минимизации функции f ( X ) = 4 (х₁ - 5)² + (х₂ - 6)² = 4x₁² + x₂² - 40x₁ - 12x₂ + 136; имеющей минимум в точке X* = {5; 6}^T . Поскольку f ( x ) зависит от двух переменных, то в начале поиска используется многоугольник с тремя вершинами. В этом примере в качестве начального многогранника взят треугольник с вершинами X₁⁽⁰⁾ = {8; 9}^T X₂⁽⁰⁾ = {10; 11}^T и X₃⁽⁰⁾ = {8; 11}^T, хотя можно было бы использовать любую другую конфигурацию из трёх точек.

На нулевом этапе поиска, k = 0, вычисляя значения функции, получаем f (8, 9) = 45, f (10, 11) = 125 и f (8, 11) = 65. Затем отражаем X₂⁽⁰⁾ = {10; 11}^T через центр тяжести точек X₁⁽⁰⁾ и X₃⁽⁰⁾ по формуле (25), который обозначим через X₄⁽⁰⁾:

x_4,1⁽⁰⁾ = 0.5 [(8 + 10 + 8) - 10] = 8;

x_4,2⁽⁰⁾ = 0.5 [(9 + 11 + 11) - 11] = 10;

с тем, чтобы получить X₅⁽⁰⁾.

x_5,1⁽⁰⁾ = 8 + 1 (8 - 10) = 6;

x_5,2⁽⁰⁾ = 10 + 1 (10 - 11) = 9;

f (6, 9) = 13.

Поскольку f (6,9) = 13 < f (8,9) = 45, переходим к операции растяжения:

x_6,1⁽⁰⁾= 8 + 2 (6 - 8) = 4;

x_6,2⁽⁰⁾ = 10 + 2 (9 - 10) = 8;

f (4,8) = 8.

Поскольку f (4, 8) = 8 < f (8, 9) = 45; то заменяем X₂⁽⁰⁾ на X₆⁽⁰⁾ и полагаем X₆⁽⁰⁾ = X₂⁽¹⁾ на следующем этапе поиска Наконец, поскольку

(1/3) [7² + 13² + 44²] ^½ = 26.8 > 10^-6;

то начинаем этап поиска k = 1. На рис. 15 показана траектория поиска на начальных этапах, а на рис. 16 изображена полная траектория поиска до его окончания. Для уменьшения целевой функции до f ( X ) = 10^-6 потребовалось 32 вычисления целевой функции.

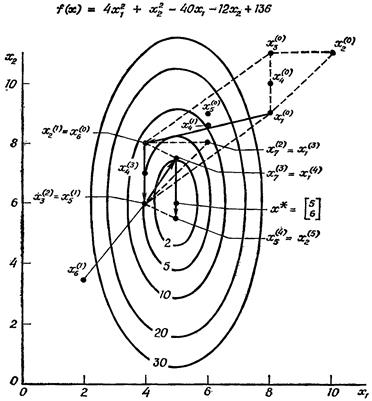
Рис. 15. Начало поиска методом Нелдера_Мида

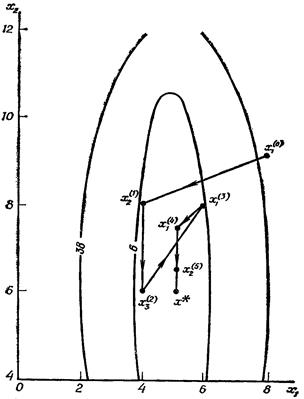
Рис. 16. Полная траектория поиска метода Нелдера-Мида.

Программа на языке С++, реализующая алгоритм Нелдера-Мида, как и ранее, представлена в виде подпрограммы, в качестве входных параметров она получает начальную точку поиска X, количество проектных переменных nx и точность поиска eps.

int Polyhedron(int nx, double x, double *opt, double eps)

//******************************************************

// Программа минимизации функции методом Нелдера-Мида

//******************************************************

// nx – количество проектных переменных

// x [] – значения проектных переменных

// opt - значение функции в точке минимума

// eps – точность поиска

//------------------------------------------------------

// Вызываемые подпрограммы

// Fx () – вычисление целевой функции

// start () – построение начального симплекса

//--------------------------------------------------------

{

extern double Fx(double);

extern void start(int, double, double*, double**);

double f[24], f_h, f_l, difer;

double x1[24][20], step, alfa, beta, gama, delta,

xnx, sum2, sums,s;

int k1,k2,k3,k4, in,i,j, index, kount;

//--------------------------------------------------

// Начальные присвоения

k 1 = nx + 1;

k 2 = nx + 2;

k 3 = nx + 3;

k 4 = nx + 4;

//--------------------------------------------

f[0] = Fx (x); // В начальной точке

//--------------------------------------------

alfa = 1.0; // Отражение

beta = 0.5; // Сжатие

gama = 2.0; // Растяжение

delta = 0.5; // Редукция

step = 1.0; // Размер симплекса

xnx = (double)nx;

// Построение симплекса в начальной точке

Start(nx, step, x, x1);

for(i = 0; i < k1; i++) {

for(j = 0; j < nx; j++) x[j] = x1[i][j];

f[i] = Fx(x);

}

M28: f_h = f[0]; f_l = f[0];

index = 0; kount = 0;

for(i = 1; i < k1; i++) {

if(f[i] > f_h) { f_h = f[i]; index = i; }

if(f[i] < f_l) { f_l = f[i]; kount = i; }

}

Вычисление центра симплекса

for(j = 0; j < nx; j++) {

sum2 = 0.0;

for(i = 0; i < k1; i++) sum2 += x1[i][j];

x1[k2-1][j] = (sum2 - x1[index][j]) / xnx;

/* Отражение */

x1[k3-1][j] = (1.0 + alfa)*x1[k2-1][j] - alfa*x1[index][j];

x[j] = x1[k3-1][j];

}

f [ k 3-1] = Fx ( x );

// Выборка второго большого значения

if (f[k3-1] >= f_l) {

if (index == 0) sums = f[1]; else sums = f[0];

for(i = 0; i < k1; i++) {

if ((index == i) || (f[i] <= sums)) continue;

sums = f[i];

}

if (f[k3-1] > sums) goto M13; else goto M14;

}

for(j = 0; j < nx; j++) { // Растяжение

x1[k4-1][j] = (1.0 - gama) * x1[k2-1][j] + gama * x1[k3-1][j];

x[j] = x1[k4-1][j];

}

f[k4-1] = Fx(x);

if (f[k4-1] < f_l) goto M16; else goto M14;

M13: if (f[k3-1] <= f_h)

for(j = 0; j < nx; j++) x1[index][j] = x1[k3-1][j];

for(j = 0; j < nx; j++) {

x1[k4-1][j] = (1.0 - beta) * x1[k2-1][j] + beta * x1[index][j];

x[j] = x1[k4-1][j];

}

f[k4-1] = Fx(x);

if (f_h > f[k4-1]) goto M16;

for(j = 0; j < nx; j++) // Редукция

for(i = 0; i < k1; i++)

x1[i][j] = delta * (x1[i][j] + x1[kount][j]);

for(i = 0; i < k1; i++) {

for(j = 0; j < nx; j++) x[j] = x1[i][j];

f[i] = Fx(x);

}

goto M26;

M16: for(j = 0; j < nx; j++)

x[j] = x1[index][j] = x1[k4-1][j];

f[index] = Fx(x);

goto M26;

M14: for(j = 0; j < nx; j++)

x[j] = x1[index][j] = x1[k3-1][j];

f[index] = Fx(x);

M26: for(j = 0; j < nx; j++) x[j] = x1[k2-1][j];

f[k2-1] = Fx(x);

difer = 0.0;

for(i = 0; i < k1; i++) {

s = f[i] - f[k2-1];

difer += (s * s);

}

difer = sqrt(difer) / xnx;

// print(x1[kount],f_l);

if (difer >= eps) goto M28;

*opt = f_l;

for(j = 0; j < nx; j++) x[j] = x1[kount][j];

return(0);

}

//==================================================

Void start(nx, step, x, x1)

int nx;

double step, x[], x1[][20];

{

double vn, step1, step2;

int i,j;

vn = (double)nx;

step1 = (step/(1.414*vn))*(sqrt(vn+1.0) + vn - 1.0);

step2 = (step/(1.414*vn))*(sqrt(vn+1.0) - 1.0);

for(j = 0; j < nx; j++) x1[0][j] = 0.0;

for(i = 1; i < nx+1; i++) {

for(j = 0; j < nx; j++) x1[i][j] = step2;

x1[i][i-1] = step1;

}

for(i = 0; i < nx+1; i++)

for(j = 0; j < nx; j++) x1[i][j] += x[j];

return;

}

//==================================================

5. Заключение

Мы рассмотрели ничтожно малое количество оптимизирующих алгоритмов. Этими алгоритмами мы показали стратегию методов поиска экстремума и теперь, на базе полученных знаний читатель может компетентно анализировать достоинства и недостатки других, существующих, а также новых методов оптимизации и уверенно выбирать подходящий алгоритм для конкретной организационно-технической задачи.

Камнем преткновения любых поисковых методов оптимизации является критерий окончания поиска. Таких критериев всего два: малое изменение функции и/или малое изменение проектных переменных. Рис. 17 иллюстрирует, почему необходимо учитывать ОБА этих критерия одновременно. Однако на практике обычно выбирается какой-либо один. Имейте это в виду.

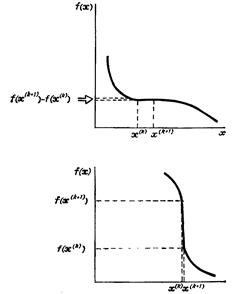
Рис. 17. Возможные ситуации при окончании поиска.

В пособии [1] рассмотрены постановки задач оптимизации и приёмы преобразования задачи с ограничениями к задаче без ограничений с помощью штрафных функций. При этом топография целевой функции безнадёжно портится и возникает проблема выбора даже не лучшего, а достаточно надёжного метода, который просто найдёт экстремум среди «оврагов» и «хребтов». Рассмотренные алгоритмы выбраны для включения в данное пособие именно с этой точки зрения. Они прошли апробацию на реальных технических задачах и со всеми испытаниями справились блестяще.

Литература

1. Данилин А.И. Основы теории оптимизации (постановки задач). Учебное пособие. –Самара: Изд-во Самарского государственного аэрокосмического ун-та, 2011. -57с.

2. Химмельблау Д. Прикладное нелинейное программирование. М: Мир, 1975. -534с.

3. Уайлд Д. Оптимальное проектирование. -М: Мир, 1981. -272с.

4. Реклейтис Г., Рейвиндран А., Рэгсделл К. Оптимизация в технике. В 2-х книгах. -М: Мир, 1986. -Кн.1 -350с.; -Кн.2 -320с.

Оглавление

1. Введение. 3

2. Классические методы_ 4

2.1. Функции одной переменной_ 4

2.2. Функции n переменных. 7

2.3. Метод Ньютона_ 9

2.4. Упражнения 13

3. Методы поиска минимума функции одной переменной_ 14

3.1.Отыскание границ интервала неопределённости_ 15

3.2. Уменьшение интервала неопределённости_ 17

3.2.1. Метод деления интервала пополам (метод дихотомии) 18

3.2.2. Метод золотого сечения. 22

3.2.3. Квадратичная аппроксимация. Метод Пауэлла. 26

3.3. Упражнения 34

4. Поисковые методы, не использующие производные 36

4.1. Прямой поиск. Метод Хука-Дживса_ 37

4.2. Метод деформируемого многогранника. 49

5. Заключение 64

Литература_ 65

Дата добавления: 2019-09-13; просмотров: 155; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 45

Мы поможем в написании ваших работ!