Метод деления интервала пополам (метод дихотомии)

Рассматриваемый метод позволяет исключать в точности половину интервала на каждой итерации. Иногда этот метод называют трёхточечным поиском на равных интервалах, поскольку его реализация основана на выборе трёх пробных точек, равномерно распределённых в интервале неопределённости. Приведём описание основных шагов поисковой процедуры, ориентированной на нахождение точки минимума функции f ( x ) в интервале (а, b ).

Шаг 1. Положить х_т = (а+ b )/2 и L = b - а. Вычислить значение f ( x_m ).

Шаг 2. Положить x ₁ = a + L /4 и x ₂ = b - L /4. Заметим, что точки х₁, х_т и х₂ делят интервал (а, b ) на четыре равные части. Вычислить значения f ( x₁ ) и f ( x ₂ ).

Шаг 3. Сравнить f ( x ₁ ) и f ( x_m ). Если f ( x ₁ ) < f ( x_m ), то исключить интервал (x_m , b), положив b = x_m. Средней точкой нового интервала неопределённости становится точка х₁. Следовательно, необходимо положить x_m = x ₁ и перейти к шагу 5.

Если f ( x ₁ ) ³ f (х_т), то перейти к шагу 4.

Шаг 4. Сравнить f ( x ₂ ) и f ( x_m ). Если f ( x ₂ ) < f ( x_m ), тоисключить интервал (а, х_т), положив а = х_т. Tак как средней точкой нового интервала становится точка x ₂, тоположить х _m = х₂ и перейти к шагу 5.

Если f ( x ₂ ) ³ f (х_т), то исключить интервалы (а, х₁) и (х₂, b ). Положить а = х₁ и b = х₂. Заметим, что х_т продолжает оставаться средней точкой нового интервала. Перейти к шагу 5.

Шаг 5. Вычислить L = b - а. Если величина | L | мала, то закончить поиск. В противном случае вернуться к шагу 2.

Замечания

1. На каждой итерации алгоритма исключается в точности по­ловина интервала поиска.

2. Средняя точка последовательно получаемых интервалов всегда совпадает с одной из пробных точек x ₁, х₂ или х_т, найденных на предыдущей итерации. Следовательно, на каждой итерации тре­буется не более двух вычислений значения функции.

3. Если проведено п вычислений значения функции, то длина полученного интервала составляет (1/2)^{n /2} величины исходного интервала.

4. В работе [3] показано, что из всех методов поиска на равных интервалах (двухточечный, трёхточечный, четырёхточечный и т. д.) трёхточечный поиск, или метод деления интервала пополам, отличается наибольшей эффективностью.

Пример 4. Метод деления интервала пополам

Минимизировать f (х) = (100 - х)² в интервале 60 ≤ х ≤ 150. Здесь a=60, b=150 и L=150 – 60 = 90.

x_m = (60+150)/2=105.

И т е р а ц и я  1.

x₁= a + (L/4) = 60+(90/4) = 82.5;

x₂=b - (L/4) = 150 - (90/4)=127.5;

f(82.5) = 306.25 > f(105) = 25;

f(127.5) = 756.25 > f(105) = 25.

Таким образом, исключаются интервалы (60, 82.5) и (127.5, 150). Длина интервала поиска уменьшается с 90 до 45.

И т е р а ц и я  2.

а = 82.5; b = 127.5; х_т=105.

L = 127.5 – 82.5 = 45;

x₁ = 82.5 + (45/4) = 93.5;

x₂=127.5 - (45/4) = 116.25;

f (93.75) = 39.06 > f (105) = 25;

f (116.25) = 264.06 > f (105) = 25.

Таким образом, интервал неопределённости равен (93.75, 116.25).

И т е р а ц и я 3.

а = 93.75; b = 116.25; x_m = 105;

 L = 116.25 – 93.75 = 22.5;

x ₁ = 99.375; x ₂ = 110.625;

f (x ₁) = 0.39 < f (105) =25.

Таким образом, исключается интервал (105, 116.25). Новый ин­тервал неопределённости равен (93.75, 105), его средняя точка есть 99.375 (точка х₁ на итерации 3). Отметим, что за три итерации (шесть вычислений значения функции) исходный интервал поиска длины 90 уменьшился до величины (90) (1/2)³=11.25.

Далее приведена программа на языке C++. Все вычисления проводятся с двойной точностью (16 десятичных цифр мантиссы чисел с плавающей точкой). Программа оформлена в виде подпрограммы и может вызываться из других программ.

# include < math . h >

double Devided_2(double *a, double *b)

{

// Программа поиска минимума на интервале [ a , b ]

// методом деления интервала пополам.

// Значение функции f ( x ) вычисляется в подпрограмме Fx ( x )

// В результате интервал неопределённости уменьшается и

// его границы доступны в вызывающей программе.

// Также «наверх» передаётся минимальное значение функции.

extern double Fx(double);

Double f, f1, f2, fm, fa, fb, x1, x2, L,

tolerance=0.00001;

// Значения функции на границах и в середине интервала

fa = Fx(*a);

fb = Fx(*b);

L = *b – *a ;

xm = (*a + *b)/2.0;

fm = Fx(xm);

// Основной цикл поиска

do {

x1 = *a + L/4.0;

x2 = * b – L/4.0;

f1 = Fx(x1);

f2 = Fx(x2);

if ( f 1 < fm ) {//Исключаем интервал [ x_m , b ]

f = f1;

* b = xm; fb = fm;

xm = x2; fm = f2;

} else {

if ( f 2 < fm ) {//Исключаем интервал [а,х _m ]

f = f2;

* a = xm; fa = fm;

xm = x2; fm = f2;

} else {//Исключаем интервалы [ а,х₁] и [х₂, b ]

f = fm

*a = x1; fa = f1;

*b = x2; fb = f2;

}

}

L = *b – *a;

} while (fabs(L) > tolerance);

return (f);

}

3.2.2. Метод золотого сечения.

Из проведённого обсуждения методов исключения отрезков интервала и минимаксных стратегий поиска можно сделать следующие выводы.

1. Если внутри интервала неопределённости количество пробных точек принимается равным двум, то их следует размещать на одинаковых расстояниях от середины интервала.

2. В соответствии с общей минимаксной стратегией пробные точки должны размещаться в интервале по симметричной схеме таким образом, чтобы отношение длины исключаемого отрезка интервала к величине интервала неопределённости оставалось постоянным.

3. На каждой итерации процедуры поиска должно вычисляться только одно значение функции в получаемой точке.

Руководствуясь этими выводами, рассмотрим симметричное расположение двух пробных точек на исходном интервале единичной длины, которое показано на рис. 6. (Выбор единичного интервала обусловлен соображениями удобства.) Пробные точки отстоят от граничных точек интервала на расстоянии τ.

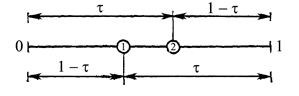
Рис. 6. Отрезки золотого сечения.

При таком симметричном расположении точек длина остающегося после исключения отрезка всегда равна τ независимо от того, какое из значений функции в пробных точках оказывается меньшим. Предположим, что исключается правый отрезок. На рис. 7 показано, что оставшийся отрезок длины τ содержит одну пробную точку, расположенную на расстоянии (1 -τ) от левой граничной точки.

Для того чтобы симметрия поискового образца сохранялась, расстояние (1 - τ) должно составлять τ -ю часть длины интервала (которая равна τ). При таком выборе τ следующая пробная точка размещается на расстоянии, равном τ -й части длины интервала, от правой граничной точки интервала, см. рис. 7.

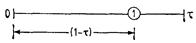
Рис. 7. Интервалы метода золотого сечения.

Отсюда следует, что при выборе τ в соответствии с условием 1 - τ = τ ² симметрия поискового образца, показанного на рис. 6, сохраняется при переходе к уменьшенному интервалу, который изображён на рис. 8. Решая это квадратное уравнение, получаем

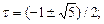                                                 (15)

откуда положительное решение τ = 0,61803... . Схема поиска, при которой пробные точки делят интервал в этом отношении, известна под названием поиска с помощью метода золотого сечения. Заметим, что после первых двух вычислений значений функции каждое последующее вычисление позволяет исключить отрезок, величина которого составляет (1 - τ)-ю долю от длины интервала поиска. Следовательно, если исходный интервал имеет единичную длину, то величина интервала, полученного в результате N вычислений значений функции, равна x^{N -1} . Можно показать, что поиск с помощью метода золотого сечения является асимптотически наиболее эффективным способом реализации минимаксной стратегии поиска.

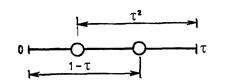
Рис. 8. Симметрия золотого сечения при уменьшении интервала

Алгоритм поиска минимума методов золотого сечения аналогичен методу деления интервала пополам, поэтому далее приведём только программу его реализации.

#include <math.h>

double Gold_Cut(double *a, double *b)

{

// Программа поиска минимума на интервале [ a , b ]

// методом золотого сечения.

// Значение функции f ( x ) вычисляется в подпрограмме Fx ( x )

// В результате интервал неопределённости уменьшается и

// его границы доступны в вызывающей программе.

// Также «наверх» передаётся минимальное значение функции.

extern double Fx(double);

---

Дата добавления: 2019-09-13; просмотров: 554; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!