Точность по величине интервала достигнута.

Выход из цикла интерполяции.

goto EXIT _;

}

// Точность по интервалу не достигнута,

// создаём новую точку

s 1 = sgn ( x [1]- x [0]); // sng () =  1, если скобки > 0

s 2 = sgn ( x [2]- x [0]); // sng () =  0, если скобки = 0

s 3 = sgn ( x [3]- x [0]); // sng () = -1, если скобки < 0

if (s1 == s2 && s1 == (-s3)) {

x [2] = x [3];

f [2] = f [3];

}

// Делаем вторую интерполяцию и

// переходим на упорядочивание

dn = (x[1]-x[2])*f[0]+(x[2]-x[0])*f[1]+(x[0]-x[1])*f[2];

ft = (f[0]-f[1])/(2.0*dn);

ft *= (x[1]-x[2])*(x[2]-x[0]);

x[3] = (x[0]+x[1])/2.0 + ft;

f[3] = Fx(x[3]);

}// Конец бесконечного цикла интерполяции

EXIT_:

*a = x[0];

*b = x[1];

return (f[0]);

}

Приведённая программа проверяет только достижение требуемой точности по величине интервала неопределённости, то есть по условию (а), однако дополнение для проверки условия (б) сделать достаточно просто, и эту модификацию программы мы предоставляем читателю.

 

3.3. Упражнения

1. Применить метод деления интервала пополам и выполнить 10 вычислений функции для определения минимума функции 2х²+3e ^{- x} на интервале (0; 1).

2. Применить метод Пауэлла для нахождения минимума функции x ⁴ – 14x ³ + 60x ² – 70x на интервале (5; 7) с точностью 0.01. Сколько раз необходимо вычислить функцию?

3. Использовать метод золотого сечения для определения минимума функции 2х²+3e ^{- x} с точностью до двух десятичных цифр. В качестве начального интервала неопределённости задать интервал (0; 1). Сколько раз необходимо вычислить функцию? Сравнить с упражнением 1.

4. Применить метод Пауэлла для определения точки минимума функции (–e^{- x} ∙ ln(x)) на интервале (1; 3) с точностью 0.001. (Проверить, не используются ли отрицательные значения х, ибо в противном случае возникнет ошибка при работе программы.)

5. Являются ли методы исключения отрезков интервалов в целом более эффективными, чем методы оценивания с использованием полиномов? Почему?

6. При реализации поисковых методов рекомендуется прини­мать решение об окончании поиска на основе проверок как величины разности значений переменной, так и величины разности значений функции. Возможна ли ситуация, когда результат одной из проверок указывает на сходимость к точке минимума, тогда как полученная точка в действительности минимуму не соответствует? Пояснить ответ рисунком.

7. Транспортное средство, которое должно курсировать на заданное расстояние, конструируется с таким расчётом, чтобы с его помощью можно было перевозить заданное количество груза в тоннах ( G ) в течение дня. Пусть стоимость транспортного средства без двигателей прямо пропорциональна грузоподъёмности транспорта (g), а стоимость двигателей плюс стоимость расхода топлива прямо пропорциональна произведению грузоподъёмности на скорость движения ( v ) в кубе. Показать, что полная стоимость транспортного средства минимальна в том случае, когда стоимость транспорта без двигателей и топлива в два раза превышает стои­мость двигателей плюс стоимость топлива. (Временем погрузки и разгрузки можно пренебречь, то есть считается, что транспорт курсирует без остановок.)

4. Поисковые методы, не использующие производные

В отличие от методов, использующих производные (или их аппроксимации), здесь рассмотрим методы оптимизации, не использующие производные. Эти методы обычно называют методами поиска, В типичном методе поиска направления минимизации полностью определяются на основании последовательных вычислений целевой функции f (х).

Как правило, при решении задач нелинейного программирования при отсутствии ограничений градиентные методы и методы, использующие вторые производные, сходятся быстрее, чем методы поиска. Тем не менее, применяя на практике методы, использующие производные, приходится сталкиваться с двумя главными препятствиями. Во-первых, в задачах с достаточно большим числом переменных довольно трудно или даже невозможно получить производные в виде аналитических функций, необходимых для градиентного алгоритма или алгоритма, использующего производные второго порядка. Хотя вычисление аналитических производных можно заменить вычислением производных с помощью разностных схем, как в программе раздела 2.3, возникающая при этом ошибка, особенно в окрестности экстремума, может ограничить применение подобной аппроксимации. Во всяком случае, методы поиска не требуют регулярности и непрерывности целевой функции и существования производных. Вторым обстоятельством, правда, связанным с предыдущей проблемой, является то, что при использовании методов оптимизации, основанных на вычислении первых и при необходимости вторых производных, требуется по сравнению с методами поиска довольно большое время на подготовку задачи к решению.

Вследствие изложенных выше трудностей были разработаны алгоритмы оптимизации, использующие прямой поиск, которые, хотя и медленнее реализуются в случае простых задач, на практике могут оказаться более удовлетворительными с точки зрения поль­зователя, чем градиентные методы или методы, использующие производные. Кроме того, при преобразовании задачи с ограничениями (задачи условной оптимизации) к безусловно экстремальной форме (к задаче без ограничений) с помощью штрафных функций [1] построенная целевая функция приобретает сложную топографию овражного характера, на которой методы, использующие производные, останавливаются преждевременно, не доходя даже до локального экстремума.

Целесообразность выбора того или иного алгоритма поиска экстремума для практического использования определяется эффективностью этого алгоритма при решении конкретного класса задач. К числу важных критериев, используемых при оценке эффективности поисковых алгоритмов, относятся следующие:

время, необходимое для реализации вычислительных процедур, или количество машинных операций;

потребная оперативная память для реализации алгоритма;

допустимая степень сложности задачи - предельное количество проектных переменных и ограничений;

точность найденного решения по отношению к оптимальному значению;

простота компьютерной программы, реализующей алгоритм;

необходимость использования производных, которые в технических задачах практически всегда приходится брать численно с помощью конечных разностей, с вынужденной потерей точности и увеличением времени поиска.

Комплексная оценка различных алгоритмов нелинейного программирования по перечисленным критериям привела к выбору для рассмотрения лишь двух алгоритмов, которые на сегодняшний день являются наиболее предпочтительными для решения организационно-технических задач с топографиями целевой функции любой сложности.

 

4.1. Прямой поиск. Метод Хука-Дживса

По существу методы поиска простейшего типа заключаются в изменении каждый раз одной переменной, тогда как другие остаются постоянными, пока не будет достигнут минимум. Например, в одном из таких методов переменная х₁ устанавливается постоянной, а х₂ изменяют до тех пор, пока не будет получен минимум. Здесь применяются алгоритмы поиска минимума функции одной переменной, рассмотренные ранее. Затем, сохраняя новое значение х₂ постоянным, изменяют х₁ пока не будет достигнут оптимум при выбранном значении х₂ и т. д. Так работает метод покоординатного спуска. Однако такой алгоритм работает плохо, если имеет место взаимодействие между х₁ и х₂, то есть, если в выражение для целевой функции входят члены, содержащие произведение х₁х₂. Таким образом, такой метод нельзя рекомендовать, если пользователь не имеет дела с целевой функцией, в которой взаимодействия не существенны.

Хук и Дживс [2]предложили другую, логически простую стратегию поиска, использующую априорные сведения и в то же время отвергающую устаревшую информацию относительно характера топологии целевой функции в эвклидовом пространстве проектных переменных Е^п [1]. Этот алгоритм включает два основных этапа: «исследующий поиск» вокруг базисной точки и «поиск по образцу», то есть в направлении, выбранном для минимизации.

Рассматриваемый алгоритм прямого поиска метода Хука-Дживса с небольшими нашими модификациями выглядит следующим образом.

1. В пространстве проектных переменных задать начальную точку 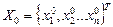 и вектор приращений . Желательно, чтобы начальная точка лежала внутри допустимой области проектных переменных. Вычислить целевую функцию f₀(X₀).

2. Из начальной точки провести исследующий поиск, при котором циклически изменяется КАЖДАЯ проектная переменная

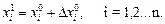                        (21)

и каждый раз вычисляется целевая функция f_i ( X ). Если приращение i-ой переменной не улучшает целевую функцию, то 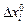 изменить на  и значение f_i(X) проверить, как и ранее. Если значение f _i (X) не улучшается ни при 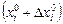, ни при 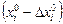, то 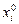 оставить без изменений.

На каждом шаге по независимой проектной переменной x_i значение целевой функции сравнивается с её значением в предыдущей точке. Если целевая функция улучшается на данном шаге, то её старое значение заменить на новое при последующих сравнениях. Однако, если проведённое возмущение по x _i неудачно, то сохранить прежнее значение f(X).

Если ни одно изменение x _i, i=1,2,...n не улучшило целевую функцию, то пробные шаги Δx _i уменьшить в два раза: Δx _i = Δx _i / 2.0. Если

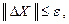                          (22)

где ε - малая, наперёд заданная величина, то осуществить выход из алгоритма; в противном случае исследующий поиск начать вновь.

В результате отыскивается точка 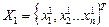 с лучшим значением целевой функции f₁(X₁).

При программной реализации этого пункта алгоритма пробные шаги по координатам x_i, i=1,2...n обычно делаются до тех пор, пока не начинается ухудшение целевой функции, см. раздел 3.1. Считается, что тем самым увеличивается скорость сходимости, поскольку новая точка X₁ будет отcтоять от X₀ на максимально возможное расстояние. В овражной ситуации этот приём, напротив, уменьшает скорость сходимости алгоритма, поскольку диагональный шаг из следующего пункта, как правило, не приводит к успеху и алгоритм приближается по своей работе к методу координатного спуска [3]. Поэтому по каждой координате x _i, i=1,2...n; будем делать только один пробный шаг.

Взаимное расположение точек X₁ и X₀ указывает новое направление в пространстве проектных переменных, которое может привести к успеху. В этом направлении делается диагональный шаг, - в формулировке Хука-Дживса - поиск по образцу:

X₂ = 2 X₁ - X₀ ;                                  (23)

и в точке X₂  вычисляется целевая функция f₂(X₂).

4. Успех или неудачу шага по образцу оценить по результатам исследующего поиска из новой базовой точки X₂. Он аналогичен поиску, описанному в пункте 2 настоящего алгоритма, и в результате определяется точка X₃ и f₃(X₃).

5. Если значение f₃(X₃) лучше, чем f₁(X₁), то поиск по образцу удачен, его провести ещё раз с некоторой корректировкой направления: X₀=X₁;  X₁=X₃; f₀(X₀) = f₁(X₁);  f₁(X₁) = f₃(X₃); и осуществить переход к пункту 3. В противном случае диагональный шаг считается неудачным и осуществить переход к пункту 2 с X₀=X₁; и f₀(X₀) = f₁(X₁).

Данный пункт алгоритма отличен от соответствующего пункта метода Хука-Дживса тем, что мы корректируем новое направление диагонального шага. В оригинале метода переход к пункту 3 проходит с X₁=X₃; f₁(X₁) = f₃(X₃); и неизменными значениями X₀ и f₀(X). Внесённая нами модификация метода делает его пригодным для поиска экстремума при овражной топографии целевой функции.

Упрощённая блок-схема алгоритма без детализации содержимого блоков представлена на рис. 9.

Пример 8. Максимизация (без ограничений) прямым поиском по Хуку и Дживсу.

Здесь мы специально показываем пример максимизации функции, чтобы подчеркнуть универсальность методов нелинейного программирования. Итак, максимизировать целевую функцию

                  

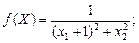
начиная из X ⁽⁰⁾ = [2.00; 2.80]^T с начальным ΔX, равным [0.60; 0.84]^T. Исходное значение f (2.00; 2,80) в базисной точке X⁽⁰⁾ равно 0.059.

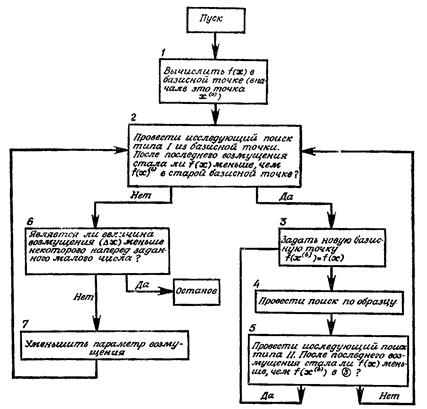
Рис. 9. Упрощённая блок-схема алгоритма Хука-Дживса

Сначала проведём исследующий поиск типа I для определения удачного направления. Такая процедура называется исследующим поиском типа I в противоположность исследующему поиску типа II, который следует за поиском по образцу. После проведения исследующего поиска типа II принимается решение по поводу того, было ли предыдущее движение по образцу успешным или неудачным.

х₁⁽¹⁾ = 2.0 + 0.60 = 2.60; f (2.60; 2.80) = 0.048 (неудача);

х₁⁽¹⁾ = 2.0 – 0.60 = 1.40; f (1.40; 2.80)^0.073 (успех);

х₂⁽¹⁾ = 2.80 + 0.84 = 3.64; f (1.50; 3.64) = 0.052 (неудача);

х₂⁽¹⁾ = 2.80 - 0.84 = 1.96; f (1.40; 1.96) = 0.104 (успех).

Исследующий поиск оказался удачным. Заметим, что при каждом поиске выбирается последний удачный вектор X. Новым базисным вектором будет (1.40; 1.96).

Теперь из точки (1.40; 1.96) проводится диагональный шаг или поиск по образцу в соответствии с правилом:

х _i ^{( k +1)} = 2 х _i ^{( k )} - х _i ^{( b )} ;

где х _i ^{( b )} – i-й компонент предыдущего базисного вектора X. В данном случае это начальный вектор X⁽⁰⁾.

х₁⁽²⁾ = 2 (1.40) - 2.00 = 0.80;

х₂⁽²⁾  = 2 (1.96) - 2.80 = 1.12;

f (0.8; 1.12) = 0.22.

Наконец проводится исследующий поиск типа II; неудача или успех его оценивается путём сравнения с f (0.8; 1.12) = 0.22:

х₁⁽³⁾ = 0.80 + 0.60 = 1.40; f (1.40; 1.12) = 0.14 (неудача);

х₁⁽³⁾ = 0.80 - 0.60 = 0.20; f (0.20; 1.12) = 0.38 (успех);

х₂⁽³⁾ = 1.12 + 0.84 = 1.96; f (0.20; 1.96) = 0.19 (неудача);

х₂⁽³⁾ = 1.12 - 0.84 = 0.28; f (0.20; 0.28) = 0.67 (успех).

Чтобы определить, оказался ли поиск по образцу успешным, сравнивают f (0.20; 0.28) = 0.67 с f (1.40; 1.96) = 0.104. Поскольку поиск по образцу успешен, то новой базисной точкой будет X⁽³⁾ = [0.20; 0.28]^T; при этом старая базисная точка представлена вектором X⁽¹⁾ = [1.40; 1.96]^T.

Затем вновь проводится поиск по образцу:

х₁⁽⁴⁾ = 2 (0.20) - 1.40 = -1.00;

х₂^{( 4)} = 2 (0.28) – 1.96 = -1.40;

f (-1.00; -1.40) = 0.51.

После этого проводится исследующий поиск типа II:

х₁⁽⁵⁾ = -1.00 + 0.60 = -0.40;    f(-0.40; -1.40) = 0.43 (неудача);

х₁⁽⁵⁾ = -1.00 - 0.60 = -1.60; f (-1.60; -1.40) = 0.43 (неудача);

х₂⁽⁵⁾ = -1.40 + 0.84 = -0,56, f(-1.00; -0.56) = 3.18 (успех).

Поскольку f (-1.00; -0.56) = 3.18 > f (0.20; 0.28) = 0.67; поиск по образцу представляется успешным и X⁽⁵⁾= [-1.00; -0.56]^T становится новой базисной точкой, а X⁽³⁾ — старой базисной точкой.

Эта последовательность поисков продолжается до тех пор, пока не будет достигнута ситуация, при которой в конце исследующего поиска типа II значение f ( X ) окажется меньшим, чем значение f ( X ^{( b )} ) в последней базисной точке. Тогда, если даже исследующий поиск типа II является успешным при одном или более возмущениях, говорят, что последний поиск по образцу неудачен и проводят из предыдущей базисной точки исследующий поиск типа I для определения нового удачного направления,

В иллюстративных целях продолжим поиск из X⁽⁵⁾= [-1.00; -0.56]^T, см. рис. 10.

Поиск по образцу:

х₁⁽⁶⁾ = 2 (-1.00) – 0.20 = -2.20;

х₂⁽⁶⁾ = 2 (-0.56) – 0.28 = -1.40;

f (-2.20; -1.40) = 0.29.

Исследующий поиск типа II:

х₁⁽⁷⁾ = -2.20 + 0.60 = -1.60; f (-1.60; -1.40) = 0.43 (успех);

х ₂ ^{( 7 )} = -1.40 + 0.84 = -0.56; f (-1.60; -0.56) = 1.49 (успех).

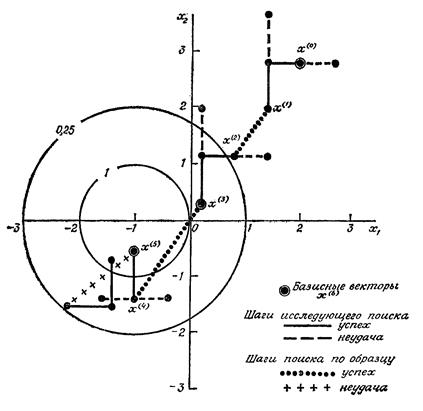
Рис. 10. Поиск максимума методом Хука-Дживса

Однако поскольку f (-1.60; -0.56) = 1.49 < f (-1.00; -0.56) = 3.18; то, несмотря на то, что исследующий поиск типа II оказался успешным, поиск по образцу считается неудачным, и из точки X⁽⁵⁾ = [-1.00; -0.56] начинают исследующий поиск типа I.

Когда достигается стадия, на которой ни исследующий поиск типа I, ни поиск по образцу (вместе с исследующим поиском типа II) не являются успешными в любом координатном направлении, говорят, что они оба неудачны и возмущение ΔX в оригинале метода Хука-Дживса уменьшают следующим образом:

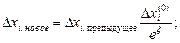                     (24)

где ξ - число последовательных неудач в исследующих поисках при данной величине шага, начиная от последнего успешного исследующего поиска.

В этом примере максимум функции равен бесконечности  

Программа на языке С++, реализующая алгоритм Хука-Дживса, как и ранее, представлена в виде подпрограммы, и, кроме того, исследующий поиск также реализован в виде подпрограммы. Для отладки программы даны строки комментариев, которые вполне работоспособны, если убрать // в начале комментария.

#include <io.h>

#include <stdio.h>

#include <fcntl.h>

#include <stat.h>

#include <process.h>

#include <math.h>

int Hooke_Jeevs(int np, double *x, double *dx, *fmin)

{

//******************************************************

// Программа минимизации функции методом Хука-Дживса

//******************************************************

// np   – количество проектных переменных

// x [] – значения проектных переменных

// dx [] – приращения проектных переменных

// fmin – найденный минимум целевой функции

//

//------------------------------------------------------

// Вызываемые подпрограммы

// Fx() – вычисление целевой функции

// poisk () – исследующий поиск из базовой точки

// pr_Fx() – отладочная печать

//------------------------------------------------------

extern void pr_Fx(int ,double*, double, unsigned, char*);

extern int Fx(int, double*, double*, unsigned*);

extern int poisk(int, double*, double*, double*, double*,

double*, unsigned*);

 

  double *x0, *x1, *x2, *x3;

Double f0,f1,f2,f3, nor_dx,

eps = 1.0 e -04; //Предельно допустимый шаг поиска

int n, i, err;

unsigned jch = 0 U ; // Счётчик количества вычислений

Целевой функции

// Выделение памяти под массивы

x0 = (double*)calloc(np, sizeof (double));

x1 = (double*)calloc(np, sizeof (double));

x2 = (double*)calloc(np, sizeof (double));

x3 = (double*)calloc(np, sizeof (double));

if (x0 == NULL || x1 == NULL || x2 == NULL || x3 == NULL)

---

Дата добавления: 2019-09-13; просмотров: 182; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!