Double Fi_der(double x, double dx)

МИНОБРНАУКИ РОССИИ

 

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ

БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«САМАРСКИЙ ГОСУДАРСТВЕННЫЙ АЭРОКОСМИЧЕСКИЙ

УНИВЕРСИТЕТ имени академика С.П. КОРОЛЕВА

(национальный исследовательский университет)»

А.И. Данилин

Методы оптимизации

 

 

Электронное учебное пособие

САМАРА

2011

УДК 51.380.115

ББК 22.18

Д 182

 

 

Данилин А. И., Методы оптимизации [Электронный ресурс] : электрон.учеб. пособие / А. И. Данилин; Минобрнауки России, Самар. гос. аэрокосм. ун-т им. С. П. Королева (нац. исслед. ун-т). - Электрон. текстовые и граф. дан. (1,4 МБайт). - Самара, 2011. - 1 эл. опт. диск (CD-ROM).

 

Рассмотрены методы поиска экстремума в самой неблагоприятной овражной ситуации. Основное внимание уделено практической реализации методов оптимизации, поэтому для каждого метода последовательно излагается теория, блок-схема и алгоритм поиска, проводится подробный разбор контрольного примера и прилагается текст программы на языке С++.

 

Учебное пособие предназначено для студентов факультета инженеров воздушного транспорта, обучающихся по направлению подготовки магистров специальностей 162300.68 "Техническая эксплуатация летательных аппаратов и двигателей" и 162500.68 «Техническая эксплуатация авиационных электросистем и пилотажно-навигационных комплексов», дисциплина «Методы оптимизации», семестр 9.

Разработано на кафедре эксплуатации авиационной техники.

 

 

© Самарский государственный

аэрокосмический университет, 2011

1. Введение.

В пособии рассмотрены методы поиска оптимальных значений максимума или минимума функции одной и п действительных переменных f (х₁, х₂, … х_п). Если функция выражает производительность, получаемую при эксплуатации самолётов типа x_i в количестве P_i,то мы будем стремиться максимизировать функцию. С другой стороны, если она выражает себестоимость эксплуатации самолёта, то мы будем стремиться минимизировать функцию. С математической точки зрения не играет существенной роли, рассматривать максимизацию или минимизацию, поскольку максимизация функции f эквивалентна минимизации (- f). Мы огра­ничимся рассмотрением минимизации.

Значения переменных могут подчиняться ограничениям или изменяться без ограничений. Если, например, они действительно выражают количество определенных эксплуатируемых самолётов, то при этом будет существовать ограничение на их производительность и на их количество, которое может позволить себе авиакомпания. Таким образом, любое решение оптимизационной задачи должно учитывать эти ограничения. В пособии рассмотрены задачи, в которых на переменные не наложены ограничения, однако в [1] показаны способы сведения задач с ограничениями к эквивалентным задачам без ограничений.

В любой практической оптимизационной задаче существует много совпадающих этапов. Наиболее важным этапом является моделирование рассматриваемой физической ситуации с целью получения математической функции, которую необходимо минимизировать, а также определения ограничений, если таковые существуют. Затем следует выбрать подходящую процедуру для осуществления минимизации. Эта процедура должна быть реализована на практике, что во многих реальных случаях вынуждает использовать компьютер для выполнения большого объема вычислений. И наконец, математический результат должен быть интерпретирован опять же в терминах физического содержания задачи. Некоторые методические рекомендации по выполнению этих этапов также рассмотрены в пособии [1].

Хотя ни одним из этих этапов нельзя пренебречь, основной упор в настоящем пособии сделан на изучение процедур, предназначенных для осуществления минимизации, и возможностей их преобразования в такие вычислительные процедуры, которые можно выполнить на компьютере.

Не случайно, что многие важные методы оптимизации были разработаны в течение последних пяти десятилетий, в период появления компьютеров, и эти методы являются машинными. Разрабатываемые алгоритмы оптимизации трудно считать сколько-нибудь практически значимыми без компьютеров, находящихся в нашем распоряжении. В настоящее время в коммерческом распространении имеются пакеты программ оптимизации, реализующие эти методы. Они могут оказаться весьма эффективными и позволят решить широкий круг задач. При этом они являются достаточно самостоятельными и могут использоваться без оценки физической сути решаемой задачи. Для большинства методов, рассматриваемых в этом пособии (причем не исчерпывающих список существующих методов), приведены программы на языке C++. Дано подробное объяснение процесса создания этих программ, что позволяет по-новому взглянуть на применимость методов оптимизации.

 

2. Классические методы

2.1. Функции одной переменной

Функция f ( x ) имеет локальный минимум в точке x ₀, если существует некоторая положительная величина δ, такая, что если    | x – x ₀ | < δ, то f ( x ) ³ f ( x ₀ ), то есть, если существует окрестность точки х₀, такая, что для всех значений х в этой окрестности f ( x ) больше f ( x ₀ ). Функция f ( x ) имеет глобальный минимум в точке х*, если для всех х справедливо неравенство f ( x ) ³ f ( x *).

На рис. 1 дано графическое представление функции f ( x ), которая имеет локальный минимум в точке х₀ и глобальный минимум в точке х*.

Рис. 1. Локальный и глобальный минимум

Классический подход к задаче нахождения значений х₀ и х* состоит в поиске уравнений, которым они должны удовлетворять. Представленная на рис. 1 функция и ее производные непрерывны, и видно, что в точках х₀ и х* производная f ʹ( x ) = df ( x ) / dx (градиент функции) равна нулю. Следовательно, х₀ и х* будут решениями уравнения

                                                                     (1)

Точка х_т, в которой достигается локальный максимум, и точка x_c,в которой имеется точка горизонтального перегиба функции, также удовлетворяют этому уравнению. Следовательно, уравнение (1) является только необ ходимым условием минимума, но не является достаточным условием минимума.

Заметим, однако, что в точках х₀ и х* производная f ʹ( x ) меняет знак с отрицательного на положительный. В точке х_т знак меняется с положительного на отрицательный, в то время как в точке х_с он не меняется. Следовательно, производная в точке минимума является возрастающей функцией, а поскольку степень возрастания f '( x ) измеряется второй производной, можно ожидать, что f "( x ₀ ) > 0, f "( x *) > 0, тогда как f "( x_m ) < 0.

Если, однако, вторая производная равна нулю, ситуация остается неопределённой.

Приведённые рассуждения могут найти надёжное обоснование, если рассмотреть разложение функции f ( x ) в ряд Тейлора в окрестности точки х₀ (или х*, или х_т), что, конечно, требует непрерывности функции f ( x ) и ее производных:

              (2)

Если в точке х₀ достигается минимум, то левая часть (2) будет неотрицательной для любого достаточно малого h ( | h | < δ ). Следовательно, первая производная f ʹ( x ) должна быть равна нулю, и это является достаточным условием, см. уравнение (1). Если бы она была положительной, то достаточно малое отрицательное значение h делало бы правую часть (2) отрицательной, а если бы она была отрицательной, то достаточно малое положительное значение h делало бы правую часть отрицательной.

Так как в следующем члене (2) всегда h ² > 0, тогда, если

                                     (3)

то в точке х₀  достигается минимум. Если f '( x ) = 0 и f "( x_m ) < 0, то из аналогичных соображений в точке х_т достигается максимум. Для определения различия между локальным и глобальным минимумами необходимо сравнить значения функций f ( x ₀ ) и f ( x *).

Неоднозначность, возникающую при равенстве нулю второй производной: , можно разрешить, увеличив количество членов в формуле разложения в ряд Тейлора:

При этом можно сформулировать следующее правило: если функция f ( x ) и ее производные непрерывны, то точка х₀ является точкой экстремума (максимума или минимума) тогда, и только тогда, когда п - четное, где п - порядок первой необращающейся в нуль производной в точке х₀. Если f ^{( n )} ( x ₀ ) < 0, то в точке x ₀ достигается максимум, если f ^{( n )} ( x ₀ ) > 0, то в точке x ₀ достигается минимум.

Пример 1. Найти точку экстремума функции f ( x ) = (х - 1)⁶.

f ʹ( x ) = 6 (х - 1)⁵ = 0 при х = 1.

Первой необращающейся в нуль производной в точке х = 1 будет f ⁽⁶⁾ (1) = (6!) > 0. Следовательно, функция f ( x ) имеет минимум в точке х = 1.

2.2. Функции n переменных.

Рассмотрим функцию п действительных переменных

        

Точка в n-мерном евклидовом пространстве с координатами х₁, х₂, х₃, ... х_п обозначается вектором-столбцом X . Градиент функции, то есть вектор с компонентами ¶f / ¶ x ₁ , ¶f / dx ₂ , … ¶f /¶x_n , обозначается Ñf ( X ) или, иногда, g ( X ). Матрица Гессе (гессиан) функции f ( X ) обозначается как G ( X ) и является симметричной матрицей (п х п)элементов вида

                             

Функция f ( X ) имеет локальный минимум в точке Х₀, если существует окрестность точки Х₀, такая, что f ( X ) больше f ( X ₀ ) во всех точках этой окрестности, то есть существует положительная величина δ, такая, что для | X — Х₀ | < δ справедливо неравенство f ( X ) > f ( X ₀ ).

В случае глобального минимума в точке X* для всех X справедливо неравенство f ( X ) > f ( X *).

При таких определениях и очевидных предположениях относительно дифференцируемости можно обобщить уравнение (2) и получить:

(4)

Тогда, если X ₀ является точкой минимума функции f(X), то каждая первая частная производная ¶f /¶x_i (i = 1,...п)должна обращаться в нуль в точке X ₀. Если это не так, то соответствующим выбором h_i можно добиться того, что разность f ( X ₀ + H ) - f ( X ₀ ) будет отрицательна.

Следовательно, необходимым условием минимума в точке X ₀ является уравнение

                   ,                                               (5)

то есть

                                                 (6)

Тогда знак разности f ( X ₀ + H ) - f ( X ₀ ) определяется членом из уравнения (4). Если матрица G ( X ₀ ) положительно определена, то этот член положителен для всех H. Следовательно, необходимыми и достаточными условиями минимума являются:

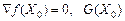        положительно определена. (7)

Необходимыми и достаточными условиями максимума являются

        отрицательно определена  (8)

Пример 2.Исследовать экстремальную точку функции f ( X) = х₁² + х₂² + х₃² – 4х₁ – 8х₂ – 12x ₃ + 100.

 при x₁ = 2; x₂ = 4; x₃ = 6.

в точке x 1 = 2; x 2 = 4; x 3 = 6 и положительно определена, поскольку определитель G ( X ) больше нуля (все собственные значения положительны и равны 2).

Следовательно, в точке X(2; 4; 6) функция f ( X ) достигает минимума.

 

2.3. Метод Ньютона

Для функций одной переменной классический подход при поиске значений х в точках перегиба функции f ( x ) состоит в решении уравнения

Решить такое уравнение не всегда просто. Поэтому кратко рассмотрим численный метод его решения. Приблизительный эскиз кривой y = f '( x ) позволит получить приближенное решение. Если можно найти два значения а и b таких, что f '( a ) и f '( b ) имеют противоположные знаки, то тогда, в силу очевидных предположений о непрерывности, будет существовать корень η настоящего уравнения, причем a < η < b , см. рис. 2.

Метод Ньютона позволяет улучшить относительно грубую аппроксимацию, чтобы получить корень уравнения φ(х) = 0. Здесь φ(х) = f '( x ). На рис. 3 точка x ₀, являющаяся координатой х точки Р, представляет собой аппроксимацию корня уравнения φ(х) = 0. Пусть РТ — касательная к кривой y = φ(х) в точке Р, а Т — точка, в которой касательная пересекает ось х.

Рис. 2. Корень уравнения y = f '( x ).

Рис. 3. Аппроксимация решения уравнения y = f '( x ).

Тогда в общем случае значение x в точке Т является лучшей аппроксимацией корня, лежащего на самом деле в точке K.

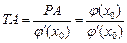Теперь ОТ = ОА - ТА =х₀ - ТА. Кроме того,  следовательно,  и соответственно

                   .                                         (9)

Аналогично можно получить улучшенное значение для 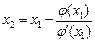 и в общем случае

                                       (10)

Итерации могут быть продолжены до тех пор, пока для двух последующих аппроксимаций не будет достигнута требуемая точность. Приведенная далее подпрограмма реализует этот алгоритм.

#include <math.h>

Double Newton(x0)

{

// Программа поиска корня функции φ ( x ) вблизи точки x 0

// Значение функции φ ( x ) вычисляется в подпрограмме Fi ( x )

// Значение производной – в подпрограмме Fi _ der ( x , dx )

extern double Fi(double);

extern double Fi_der(double, double);

double fi, x_current, x, dx=0.001, derivative,

tolerance=0.0001;

x_current = x0;

do {

x = x_current;

fi = Fi(x_current);

derivative = Fi_der(x,dx);

x_current = x – fi/derivative;

}

while (fabs(x_current – x) > tolerance);

return ( x );

}

Универсальность программы достигается за счет того, что функция fi = φ(х) вычисляется в подпрограмме Fi ( x ), а производная функции derivative = φ '( x ) вычисляется в подпрограмме Fi _ der ( x , dx ) для произвольного значения х. Точность решения задаётся переменной tolerance.

Если в подпрограммах Fi ( x ) и Fi _ der ( x , dx ) вычислять соответственно первую и вторую производную функции f ( x ), то мы найдем точку её экстремума. Если функции f ( x ) и φ(х) заданы аналитически, то параметр dx при вычислении их производных не нужен и в соответствующих подпрограммах его можно не использовать. В общем случае, когда аналитическое выражение для функции неизвестно, производная может быть вычислена с помощью конечных разностей, например:

double Fi_der(double x, double dx)

{// Вычисление производной с помощью

Центральной разностной схемы

extern double Fi ( double );

return((Fi(x+dx)- Fi(x-dx)/(2*dx));

}

Рис. 4. «Раскачка» метода Ньютона

Применение метода Ньютона будет неудачным, если первая аппроксимация корня такова, что отношение φ(х)/ φ '( x ) недостаточно мало, то есть мы «проскочим» корень уравнения  y =φ(х), см. рис. 4. Для того чтобы итерации сходились, в общем случае необходимо улучшить начальную аппроксимацию корня, - положение точки P ₀.

2.4. Упражнения

1. Найти значения максимума и минимума функции f ( x ) = х (х-1)².

2. Найти значения максимума и минимума функции f ( x ) = х / (х²+1).

3. Показать, что минимальным значением функции y ( q ) = ( a cos q + b sin q ) является . Можно ли получить этот результат, не используя производных?

4. Равнобедренный треугольник с вертикальным углом 2 q вписан в окружность радиуса R . Найти выражение для площади треугольника как функции от q и показать, что она максимальна, когда треугольник равносторонний, то есть q = 30⁰.

5. Исследовать функцию  Нарисовать её график. Показать, что f (x)имеет минимум при х = 0. Чему равно значение f '(x) при х = 0 ? Меняет ли знак f '(х), если х возрастает при прохождении через 0 ?

6. Исследовать функцию f (x) = | x |. Найти её минимум. Что можно сказать относительно поведения f '( x ) в точке минимума ?

7. Исследовать точки перегиба функции f ( x ) = х⁴- 14х³ + 60х² – 70x. Этот кажущийся простым пример иллюстрирует одну из классических задач. Требуется решить уравнение f '( x ) = 0. В данном случае оно является кубическим уравнением, которое не так просто раскладывается на множители. Здесь надо применить метод Ньютона для нахождения точек перегиба функции f ( x ), но предварительно надо найтихорошее приближение к ним.

8. Исследовать точки перегиба функции

9. Исследовать точки перегиба функции

10. Пусть f ( X ) есть квадратичная функция вида

    

где а — константа; b — вектор, не зависящий от X, a G - положительно определенная симметричная матрица, не зависящая от X. Показать, что точка минимума квадратичной функции f ( X ) имеет координаты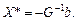

11. Показать, что функция f ( X ) = ( x ₁ — а)² + (х₂ — b )² + (х₃ — с)² имеет минимум в точке X*(а, b , с).

 

3. Методы поиска минимума функции одной переменной

Упражнение 7 раздела 2.4 иллюстрирует общую задачу, возникающую при классическом подходе. Уравнение f '( x ) = 0 не решается простым способом, и поэтому мы вынуждены прибегать к численным методам. Рассмотрим несколько простых численных процедур, непосредственно локализирующих минимум функции f ( x ).

С помощью численных методов мы непосредственно ищем минимум функции f(x) в некотором интервале а ≤ х ≤ b, в котором, как предполагается, лежит минимум, вычисляя значения функции в выбранных точках данного интервала. Несомненным достоинством поисковых методов такого рода является то, что они основаны лишь на вычислении значений функций. При этом не требуется, чтобы исследуемые функции были дифференцируемы; более того, допустимы случаи, когда функцию нельзя даже записать в аналитическом виде. Единственным требованием является воз­можность определения значений функции f(x) в заданных точках х с помощью прямых расчётов или имитационных экспериментов.

Вообще в процессе применения рассматриваемых методов поиска можно выделить два этапа:

этап отыскания границ интервала неопределённости, на котором реализуется процедура поиска границ достаточно широкого интервала, содержащего точку оптимума;

этап уменьшения интервала, на котором реализуется конечная последовательность преобразований исходного интервала с тем, чтобы уменьшить его длину до заранее установленной величины.

3.1.Отыскание границ интервала неопределённости

На этом этапе сначала выбирается исходная точка, а затем на основе правила исключения строится относительно широкий интер­вал, содержащий точку оптимума. Обычно поиск граничных точек такого интервала проводится с помощью эвристических методов поиска, хотя в ряде случаев можно также использовать методы экстраполяции. Обычно это шаговый процесс, при котором из некоторой начальной точки делается серия шагов по аргументу и вычисляется функция. Процесс продолжается до того момента, когда функция начнёт возрастать. Это признак того, что точка минимума пройдена и последние три точки задают интервал неопределённости, содержащий минимум функции, см. рис. 5.

В зависимости от способа выбора шага различают разные виды поиска. Если, например, шаг постоянный, то говорят о равномерном поиске. В соответствии с другим эвристическим методом, который был предложен Свенном [2,3], (k+1) пробная точка определяется по рекуррентной формуле

                    (11)

где х₀ - произвольно выбранная начальная точка, Δ - подбираемая некоторым способом величина шага. Знак Δ определяется путём сравнения значений f ( x ₀ ), f (х₀+|Δ|) и f (х₀-|Δ|). Если

f (х₀-|Δ|) ³ f ( x ₀ ) ³ f (х₀+|Δ|),                          (12)

то, согласно предположению об унимодальности функции, точка минимума должна располагаться правее точки х₀ и величина Δ выбирается положительной. Если изменить знаки неравенств на противоположные, то для Δ следует выбирать отрицательное значение. Если же

f (х₀-|Δ|) ³ f ( x ₀ ) ≤ f (х₀+|Δ|),                                        (13)

то точка минимума лежит между (х₀-|Δ|) и (х₀+|Δ|) и поиск граничных точек завершён. Случай, когда

f (х₀-|Δ|) ≤ f ( x ₀ ) ³ f (х₀+|Δ|),                                        (14)

противоречит предположению об унимодальности. Выполнение этого условия свидетельствует о том, что функция не является уни­модальной.

Рис. 5. Интервал неопределённости

Пример 3. Рассмотрим задачу минимизации функции f (х)=(100 - х)² при заданной начальной точке х₀ = 30 и величине шага |Δ| = 5. Знак Δ определяется на основе сравнения значений:

f ( x ₀ )    = f(30) = 4900;

f (х₀+|Δ|) = f(35) = 4225;

f ( x ₀ - |Δ|) = f(25) = 5625.

Так как       f (х₀-|Δ|) > f ( x ₀ ) > f (х₀+|Δ|),

то величина Δ должна быть положительной, а координата точки минимума х* должна быть больше 30. Имеем x ₁ = x ₀ + Δ = 35. Далее x ₂ = x ₁ + 2Δ = 45, f(45) = 3025 < f ( x ₁ ),

откуда x* > 35.

х₃= x ₂ + 2² Δ = 65,     f(65) = 1225 < f(x₂),

откуда х* > 45.

х₄= x ₃ + 2³Δ = 105, f(105) = 25 < f(x₃),

откуда х* > 65.

х₅=х₄ + 2⁴ Δ = 185, f(185) = 7225 > f(х₄),

следовательно, x* < 185. Таким образом, шесть шагов вычислений х* позволили выявить интервал неопределённости 65 ≤ x* ≤ 185, в котором расположена точка минимума х*. Заметим, что эффективность поиска граничных точек непосредственно зависит от величины шага Δ. Если Δ велико, то получаем грубые оценки координат граничных точек, и построенный интервал оказывается весьма широким. С другой стороны, если Δ мало, для определения граничных точек может потребоваться достаточно большой объем вычислений.

3.2. Уменьшение интервала неопределённости

После того как установлены границы интервала неопределённости, содержащего точку минимума, можно применить более сложную процедуру его уменьшения с целью получения уточнённых оценок координат минимума. Величина отрезка интервала, исключаемого на каждом шаге, зависит от расположения пробных точек х₁ и х₂ внутри интервала неопределённости. Поскольку местонахождение точки минимума заранее неизвестно, целесообразно предположить, что размещение пробных точек должно обеспечивать уменьшение интервала в од­ном и том же отношении. Кроме того, в целях повышения эффек­тивности алгоритма необходимо потребовать, чтобы указанное от­ношение было максимальным. Подобную стратегию иногда назы­вают минимаксной стратегией поиска.

---

Дата добавления: 2019-09-13; просмотров: 232; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!