Ряд Фурье можно записать в экспоненциальной форме

Для непериодических процессов не существует периода и его нельзя характеризовать дискретным спектром, т.к. спектр непрерывен, тогда

Эти две формулы называют парным преобразованием Фурье
Амплитудный спектр единичного прямоугольного импульса (как частный случай нестационарного процесса) с амплитудой Аои продолжительностьюТ:

Как видно амплитудный спектр прямоугольного импульса сплошной.
Таким образом, из рассмотренных рассуждений можно сделать следующие выводы:
1. Любой динамический процесс характеризуетсяамплитудными и спектральными характеристиками.
2. Периодический синусоидальный процесс характеризуется амплитудой и периодом колебаний иличастотой.
3. Любой периодический процесс можно представить в виде суммы синусоидальных составляющих сразными амплитудами и фазами.
4. Сложный периодический процесс можно разложить на синусоидальные составляющие, которыеможно представить в виде амплитудного спектра - зависимости амплитуд частотных составляющих от значений частоты этих составляющих или номера гармоник.
5. Амплитудный спектр периодического процессадискретный. Ненулевые амплитуды составляющихимеются на частотах, кратных первой гармоники.
6. Одноточный импульс с длительностьюТимеет сплошной спектр - ненулевые амплитуды составляющих имеются на всех частотах. До 90% энергииодиночного импульса сосредоточено в полосе частот от0 до — Гц. Энергия всех составляющих импульса определяется как
|
|
|
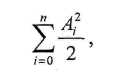
где Aj- амплитуда составляющей на i-ой частоте,
п - количество частот.
7. Периодическая последовательность одиночных импульсов имеет дискретный спектр.
Огибающая, проведённая через амплитуды частотных составляющих, имеет форму одиночного импульса.
8. Случайный динамический процесс характеризуется функцией спектральной плотности и для процесса, представленного аналитически определяется через преобразование Фурье. Функция спектральной плотности характеризует распределение энергии случайного процесса по частотам. Поскольку спектр такого процесса сплошной, то энергия этого процесса в диапазоне fi + i ~ fiраспределяется на узкий диапазон А/ и является значением функции спектральной плотности при значениях частоты f {.

Исследование сигналов в частотной области
Для точного определения характера неисправности необходимо понимание физической сущности сигналов, которые вы собираетесь анализировать, и чёткое представление о возможностях спектрального анализа.
Спектральный анализ предназначен для выявления динамических характеристик измерительных сигналов и выполняется в частотной области. Строя спектр, вы тем самым раскладываете исходный сигнал по составляющим его синусоидальным сигналам с разной частотой и амплитудой. Обычно эти методы применяют для тех или иных колебательных систем. Например, нелинейные искажения, обусловленные высшими гармониками, сложно определить по форме сигнала во временной области. Получив спектр, вы сразу видите гармонические составляющие, можете вычислить их амплитуду и величину искажения исходного сигнала.
|
|
|
Аналого-цифровое преобразование
В основе компьютерного спектроанализатора всегда лежит программное обеспечение, осуществляющее вычисление спектра. Поскольку компьютер оперирует цифровыми данными, требуется преобразовать исходный сигнал в цифровой ид. Такое преобразование следует выполнять с достаточной точностью, чтобы не получить значительных искажений. В любом случае аналоговый сигнал и его оцифрованный эквивалент несколько отличаются. В зависимости от частоты оцифровки теряется некоторая часть исходного сигнала, лежащая между двумя точками дискретизации. Разрешающая способность АЦП определяет точность представления амплитуды исходного сигнала в цифровом виде.
|
|
|
Имеется специальная теория цифровой обработки сигналов, которая изучает вопросы, связанные с преобразованием сигналов в цифровой вид и их последующим математическим анализом.
Обычно в диагностических приборах определяется амплитудой спектр или спектр среднеквадратических значений частотных составляющих как

| Определение | Описание | Примечание |
| Аналоговый фильтр против наложения спектров | - НЧ фильтр перед АЦП - Частота среза должна выбираться так чтобы исключить составляющие, лежащие выше половины частоты оцифровки | - Исключает наложение высокочастотных составляющих, возникающих при оцифровки - Дополнительные участки спектра (неустраняемые цифровыми способами) накладываються на ваш входной сигнал |
| Полоса пропускания | Диапазон частот, который требуется анализировать | Частота оцифровки и фильтр против наложения спектров должны соответствовать требуемой полосе пропускания |
| Частота оцифровки | Число измерений, которые ваш прибор может проводить за 1 сек. | Определяет минимальную частоту в спектре |
| Динамический диапазон | - Обычно выражается в дБ - Отношение максимально определяемого сигнала к пиковому значению уровня шума(NF) | Показывает возможности оборудования по измерению малых сигналов по отношению к большим |
| Разрешающая способность (nбит) | - Указывает число уровней дискретизации амплитуды измеряемого сигнала - Число уровней | - определяет теоретический порог для динамического диапазона - Отношение сигнал/шум |
| Плотность входного шума (ND) | - Выражается в дБ/Гц - Уровень шума (или его мощность), присутствующая в 1 Гц полосы пропускания входного сигнала | Зная плотность шума и частотное разрешение, вы можете вычислить уровень шума NF=ND+10Log(f) |
| Параллельные измерения | - Измерения, проводимые одновременно по нескольким каналам | Сохраняют фазовые зависимости между каналами, что позволяет вычислять их корреляцию |
| Программируемое усиление | Возможность задавать требуемое усиление входного сигнала | - Устанавливая нужное усиление можно полнее использовать динамический диапазон входного сигнала - Идея- обеспечение на входе АЦП сигнала, диапазон которого как можно ближе соответствует входному диапазону АЦП |
| Согласование сигналов | Возможность преобразования вида входного сигнала и опорные источники для датчиков | Многие первичные преобразователи требуют внешнего питания |
| Время измерения | Время накопления в памяти результатов измерения, ограниченное объемом памяти жесткого диска | Определяет частотное разрешение f=1/T |
|
|
|
Вычисление результата
Получаемая вами выборка измерительного сигнала содержит значения амплитуды этого сигнала, полученные через определённые (обычно одинаковые) промежутки времени. Чтобы получить спектр (исходный сигнал в частотной области), следует выполнить преобразование Фурье. Обычно используются алгоритмы быстрого преобразования Фурье (БПФ). Эти алгоритмы входят в состав библиотек математического анализа математических пакетов, таких как LabVIEW, Match-Cad и MathLab. На их основе вычисляются АЧХ, ФЧХ, импульсная характеристика и т.д.
С точки зрения ПК входные и выходные массивы для алгоритмов БПФ представляют собой просто набор чисел в памяти. Однако вы можете осмыслить эти данные, поскольку обладаете информацией по ходу измерения. Это частота оцифровки (fs), общее время оцифровки (Г) и число результатов измерения ( N ). Они определяют максимальную частоту для анализа (/тах) и частотное разрешение ( fres). Эти параметры определяют теоретический предел точности анализа. Однако, чтобы на реальной задаче обеспечить требуемую точность, следует проводить измерения с несколько большей частотой и длительностью. Поэтому некоторые измерительные устройства автоматически обеспечивают для вас нужный запас.
Измерения, вычисления ирреальная полоса пропускания
Скорость работы программного обеспечения всецело зависит от быстродействия вашего ПК. Возможно, вы имеете представление о такой характеристике, которая основана на скорости измерения и последующих вычислениях. Для специализированных спектроанализаторов, выполненных в виде законченных приборов, такая характеристика может быть легко установлена. Для компьютерных систем дело обстоит сложнее. Здесь ключевая роль заключается в числе измерительных каналов, скорости процессора, общей загруженности системы. Ведь ваш компьютер, параллельно кроме выполнения чисто измерительных задач и вычисления спектра, производит массу другой работы.
На приведённой диаграмме показывается зависимость быстродействия компьютерного спектроанализатора в зависимости от числа каналов. Тестирование заключалось в выполнении измерений платами АЦП и вычислений БПФ по 1024 точкам на контроллере PentiumIII 1.26 ГГц.
Применение второго процессора повысило быстродействие всей системы примерно на 70-80%.
Дата добавления: 2019-09-13; просмотров: 448; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
