МЕТОДЫ ПРЕОБРАЗОВАНИЯ И ОБРАБОТКИ ДИАГНОСТИЧЕСКИХ
СИГНАЛОВ
3.1. Понятие о квантовании аналогового сигнала
Большинство величин в природе изменяются непрерывно и обозначаются U { t ), где t- время. По техническим причинам вместо сигнала U \ t ) регистрируются равномерно распределённые отсчёты Unфункции U \ t ). Когда берутся отсчёты, они не регистрируются с бесконечной точностью, а округляются или урезаются до необходимого количества знаков. Эта процедура называется квантованием отсчётов. Квантованные отсчёты подвергаются дальнейшей обработке. Цель этой обработки - получить связь функции Unс наблюдаемыми явлениями. Необходимо подчеркнуть, что отсчёты предполагаются равномерно распределёнными. В замерах Unсодержатся ошибки или помехи.
Последовательность чисел { l / n } будем обозначать как Un = U ( n ), где п - целое число.
Дискретизация и квантование сигнала.
Дискретизация по времени представляет собой последовательность, элементы которой U ( kT ) в точностиравны соответствующим значениям непрерывного сигнала. Дискретизация по уровню называется квантованием. Примером дискретного сигнала может быть последовательность импульсов с изменяющейся амплитудой - АИМ колебания.
Аналитически это записывается в форме
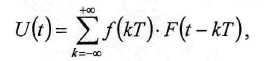 где F ( t - кТ) - единичный импульс.
где F ( t - кТ) - единичный импульс.
Если уменьшать длительность импульса F ( t ), сохраняя площадь неизменной, то в пределе F [ t ) стремится к дельте функции (5 -функция) и тогда выражение для дискретного сигнала можно представить в виде
|
|
|
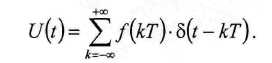
Для преобразования аналогового сигнала в цифровой после дискретизации по времени должна следовать дискретизация по уровню j[KBaHTOBamie). Необходимость квантования вызвана тем, что любое вычислительное устройство может оперировать только числами, имеющими конечное число разрядов. Таким образом, квантование представляет собой округление передаваемых значений с заданной точностью.
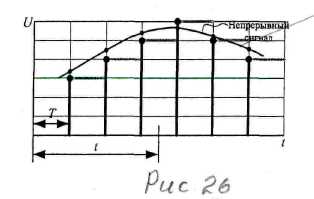
Сигнал, дискретизированный по времени и по уровню называется цифровым.
Правильный выбор интервалов дискретизации по времени и по уровню очень важен при разработке цифровых систем обработки сигналов.
Чем меньше интервал дискретизации, тем точнее дискретизированный сигнал соответствует исходному непрерывному. Однако при этом возрастает число отсчётов и для сохранения общего времени обработки сигнала приходится увеличивать скорость обработки, что не всегда возможно. Для уменьшения интервала квантования требуется большее число разрядов для описания сигнала.
3.2. Пример устройства цифровой обработки сигнала
Существует очень много разнообразных цифровых систем обработки сигналов различного назначения. Но они содержат некоторые специфические общие элементы.
|
|
|
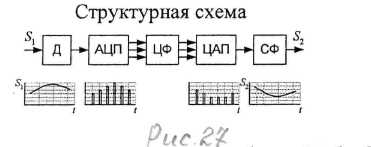
Система цифровой обработки сигнала должна содержать устройство для преобразования аналогового сигнала в цифровой. Такое устройство обычно состоит из дискретизатора,непрерывного сигнала по времени и аналого-цифрового преобразователя (АЦП) превращающего выборочное значение сигнала в числовую последовательность, элементы которой - числа, представленные в коде вычислительной машины. Этот цифровой сигнал уже готов для цифровой обработки.
Далее следует электронное вычислительное устройство, в котором происходит цифровая обработка цифрового сигнала по заданному алгоритму. Алгоритм обработки может быть разнообразным. Цифровые устройства, производящие линейную обработку сигнала называется цифровыми фильтрами/,~ Ц, гр
Сигнал на выходе фильтра имеет вид последовательности чисел, представленных в коде ЭВМ. Дальнейшая обработка зависит от назначения сигнала. Например, если нужен сигнал для управления аналоговым устройством, то он должен быть преобразован в аналоговый с помощью цифро-аналогового преобразователя (ЦАП) и выходного сглаживающего фильтра (см. схему).
|
|
|
3.3. Выбор параметров дискретизации непрерывных сигналов
При преобразовании сигналов из аналоговой в цифровую форму очень важен правильный выбор интервалов дискретизации. Слишком редкие отсчёты исключают резкие изменения сигнала и если они являются помехами, то это полезно. В противном случае исключение резких изменений сигнала приводит кпотериинформации. Слишком частые отсчёты исключают потерю информации, приводят к большому объёму значений сигнала, который зачастую является избыточным.
Задача о выборе интервала дискретизации наиболее просто решается для сигнала с ограниченным спектром на основании теоремы Котельникова-Шеннона, или теории отсчётов.
В соответствии с этим непрерывный сигнал f { t ),
в спектре которого не содержится частот выше /в, полностью описывается выборочными значениями f ( kT ), отсчитанными через интервалы времени.
Аналитически это выражение в виде ряда Котельникова выглядит как
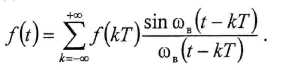 Интервал времени Т между соседними отсчётами называется .интервалом Котельникова или интервалом Найквиста.
Интервал времени Т между соседними отсчётами называется .интервалом Котельникова или интервалом Найквиста.
Таким образом, вместо непрерывного сигнала с ограниченным спектром можно рассматривать дискретную последовательность значений f ( kT ). Причёминтервал дискретизацииТдолжен быть не более
|
|
|
Если отсчёты взять реже, то это может привести к ошибкам.
Практически все реальные сигналы имеют конечную длительность и поэтому спектр их безграничен. Для таких сигналов невозможно указать значение /в.выше которых спектр тождественно равен 0. Это означает, что при любом значении частоты дискретизации/ или шв, или интервала дискретизации 1 = — последовательность дискретных отсчётов описывает исходный непрерывный сигнал с некоторой ошибкой. Величина этой ошибки определяется частью спектра сигнала, соответствующей частотам, выше соо.
Дискретизация прямоугольного импульса с амплитудойАи длительностью Ги
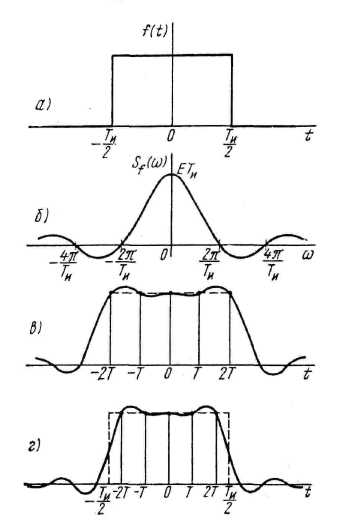

Выводы:
1. Импульсы с резкими границами (типа прямоугольного) имеют медленно убывающий
спектр и их дискретизация затруднительна.
2. Подбором частоты дискретизации можно добиться более точного представления сигнала.
3. На практике сигналы с широким спектром пропускают через аналоговый фильтр, ограничивая тем самым спектр сигнала и далее применяют преобразование его в цифровую форму счастотой квантования превышающей граничную частоту «среза» фильтра примерно в 2раза.
Цифровая фильтрация включает в себя процессы сглаживания, предсказания, дифференцирования, интегрирования, разделения сигналов и вычитания помех из сигналов.
3.4. Понятие о методах обработки диагностических сигналов
Для того чтобы поставить диагноз объекту диагностирования необходимо получить диагностические признаки технического состояния.
Диагностические признаки связаны со структурными параметрами.
Диагностические признаки можно получить путём специальной обработки динамических процессов получаемых в диагностических точках.
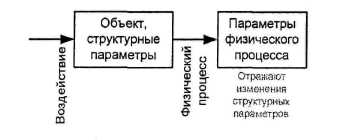
Любой динамический процесс A ( t ) характеризуется амплитудными и спектральными характеристиками.
Если процесс периодический или гармонический, то его характеристиками являются амплитуда, период и частота.
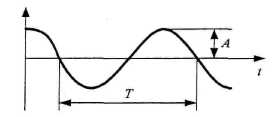
Обычно на практике встречаются многочастотные процессы как периодические так и непериодические. В первом приближении этот процесс можно характеризовать максимальным значением.
К непериодическим процессам относятся случайные процессы и сумма случайных и периодических процессов.
Независимо от характера динамического процессаизменяется их амплитудная и специальная обработка.
Целью этой обработки является изучение структурысоставляющих сигнала, как по амплитудам, так и по частотам.
(При периодических процессах для получения этих характеристик применяют разложение в ряд Фурье.)Рядом Фурье является функция в виде:
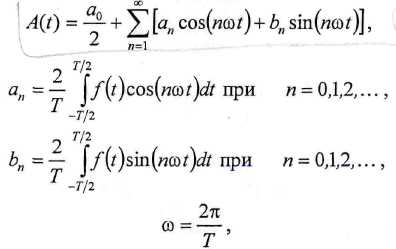
Из уравнений видно, что периодическая функция может быть представлена косинусоидальныхсоставляющих с частотами, кратными основной частоте 2тгТ '
Зависимость спот называется амплитудным спектром функции A \ t ). Зависимость фазы \\ inотназывается фазовым спектром.
а0- среднеарифметическое значение за интервал Т.
Графики функций спи \\ inот «ш являются дискретными и изображаются прерывистыми функциями.
Рассмотрим спектр функции

гдеТ - период периодической функции.
Функции f { t ) можно придать другой вид
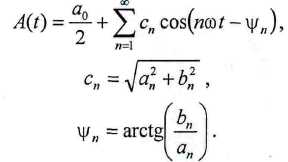
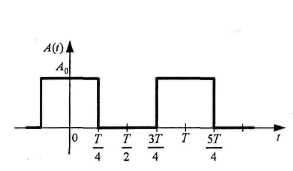
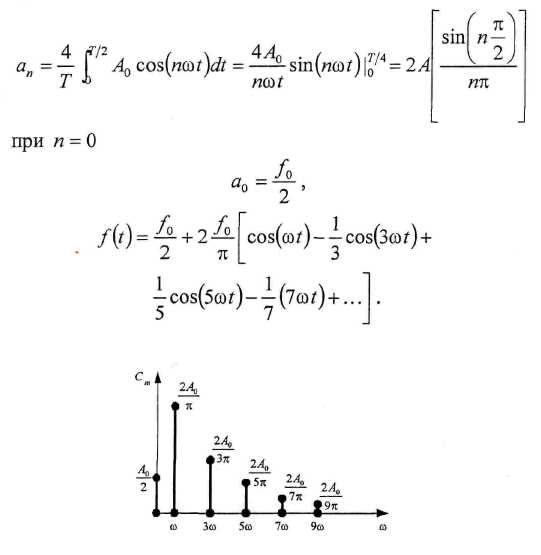
Функция A ( t ) чётная и поэтому ряд Фурье будет состоять из чётных функций: при и = 1,2,...
Дата добавления: 2019-09-13; просмотров: 340; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
