Экстремум функции 2 переменных.
Рассмотрим функцию z=f(x;y) двух переменных, определённую в некоторой области D.
Определение: Функция f(x;y) имеет строгий локальный максимум (минимум) в точке 
, если неравенство 
имеет место во всех точках 
из некоторой достаточно малой окрестности точки 
.
Определение: Функция f(x;y) имеет экстремум в точке, если эта функция имеет максимум или минимум в этой точке.
Необходимые условия экстремума.
Если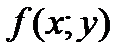 
дифференцируема в точке 
и имеет экстремум в этой точке, то её дифференциал равен нулю: 
Определение: Точка называется стационарной точкой функции 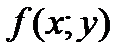, если 
Пусть -стационарная точка функции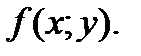 
Обозначим 
Достаточные условия экстремума.
1.Если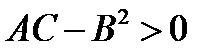 
и 
, то 
-точка максимума.
2.Если 
и 
, то 
-точка минимума.
3.Если 
, то -не является точкой экстремума.
4.Если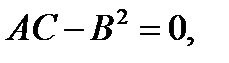 
то точка 
может как быть, так и не быть точкой экстремума, поэтому требуется дополнительное исследование.
Пример:
Исследовать на экстремум: 
Решение:
Найдем частные производные заданной функции:
; 
. Единственной стационарной точкой является точка 
(Которая получена при решении системы 
и 
).
Найдем частные производные второго порядка:
; 
; 
Так как 
то точка не является точкой экстремума.
Пример:
Исследовать на экстремум: 
Решение:
Найдем частные производные заданной функции:
; 
. Стационарными точками являются точка 
и 
(Которые получены при решении системы и 
).
|
|
|
Найдем частные производные второго порядка:
; 
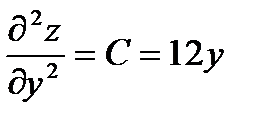; . Рассмотрим выражение вида: 
. В точке - экстремума нет, поскольку . В точке наблюдается минимум, так как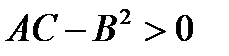 
и 
.
Наибольшее и наименьшее значение функции в замкнутой области.
Пусть функция z = f ( x , y ) непрерывна в замкнутой ограниченной области D, границей которой является кривая L, тогда по первой теореме Вейерштрасса функция ограничена в замкнутой области, а по второй - достигает в области своего наибольшего и наименьшего значения. Эти значения могут быть среди точек экстремума, принадлежащих области и на границе области D.
Производная по направлению и градиент.
Рассмотрим функцию 
в некоторой области D.
Пусть точка M0(x0, y0)ÎD. Рассмотрим вектор 
с началом в точке M0. Направление вектора задают две направляющих косинуса: 
и 
- это направляющие вектора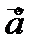 
. Причем cos2a+cos2b=1, 
- это единичный вектор направляющие l имеет координаты l0(cos a, cos b). Дадим вдоль вектора l приращение Dl (x0, y0).
Функция получит полное приращение.
, разделим 
на 
и перейдём к пределу 
.
Определение: Производной f ( x , y ) по направлению `l в точке M0 называют число 
так как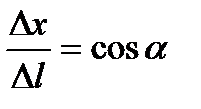 
, 
.
|
|
|
Если дана функция трех переменных u=u(x,y,z), точка M0(x0,y0,z0), `l ={x,y,z}. Тогда производная по направлению имеет вид 
, где направляющие cos: 
, 
, 
.
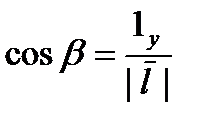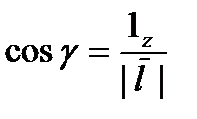Определение: Градиентом функции u=u(x,y,z) в точке M0 называют вектор, имеющий своими координатами значение частных производных функции в точке M0.
Обозначается: 
= 
С одной стороны производная по направлению равна скалярному произведению градиента функции на вектор `l0: 
. С другой стороны : 
= 
grad u.
Если ` 
, то производная по направлению равна нулю.
Если ` 
, то производная по направлению принимает максимальное значение.
Вывод: градиент функции показывает направление наискорейшего возрастания функции в точке.
Пример: Вычислить: производную по направлению, градиент функции и длину градиента.
, M0(1, 1, 1), `l={1, 2, -2}.
Решение :
; 
; 
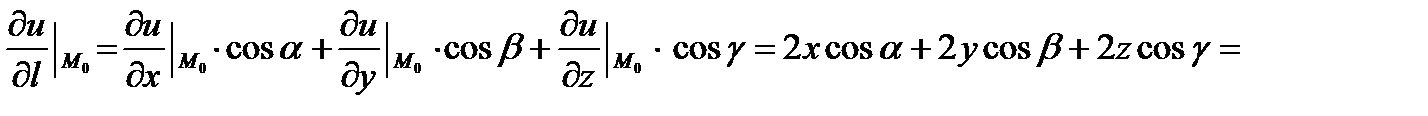
Определение: Пусть в пространстве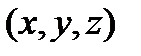 
имеется область D в которой задана функция 
. В этом случае говорят о скалярном поле, заданном в области D.
Определение: Рассмотрим точки области в которых функция принимает одинаковое значение 
. Множество таких точек образуют некоторую поверхность, называемую поверхностью уровня.
В случае функции двух переменных поверхностями уровня являются линии на плоскости 
. Если значения функции представлять как значения на оси 
: 
то линиями уровня на плоскости будут проекции линий пересечения поверхности с плоскостью 
.
|
|
|
Градиент всегда направлен перпендикулярно к линиям уровня, следовательно, является направляющим вектором нормали к заданной поверхности в фиксированной точке.
Дата добавления: 2019-09-13; просмотров: 169; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!