Частные производные функций 2 переменных и их геометрический смысл.
Пусть функция  определена в окрестности точки M(x,y) и в самой точке М. Дадим переменной x приращение Dx (x®x+Dx), а переменную y оставим без изменения (y®y)так, чтобы точка M1(x+Dx; y)Îуказанной окрестности, тогда функция получит приращение Dxz по переменной x:
определена в окрестности точки M(x,y) и в самой точке М. Дадим переменной x приращение Dx (x®x+Dx), а переменную y оставим без изменения (y®y)так, чтобы точка M1(x+Dx; y)Îуказанной окрестности, тогда функция получит приращение Dxz по переменной x:  .
.
Определение: Если существует предел при Dx®0 отношения приращения функции к приращению аргумента, то он называется частной производной функции z по переменной x и обозначается 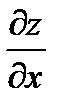 :
:  .
.
Определение: Если существует предел при 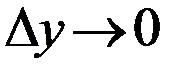 отношения приращения функции к приращению аргумента, то он называется частной производной функции z по переменной y и обозначается
отношения приращения функции к приращению аргумента, то он называется частной производной функции z по переменной y и обозначается 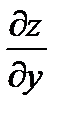 :
:  .
.
При вычислении частных производных все переменные, кроме одной (по которой берется производная) считаются константами. Берем функцию двух переменных, частное по x, y – константа.
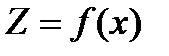 ,
,  y-const.,
y-const., 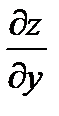 x-const или
x-const или 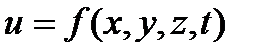
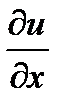 y,z,t-const.,
y,z,t-const.,  x,y,t-const..
x,y,t-const..
Пример:
Вычислить частные производные функции двух переменных.
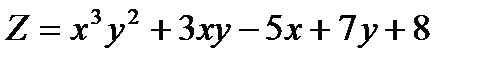 ;
;
Решение:
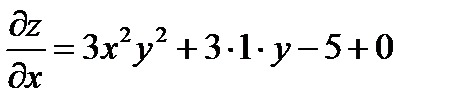 ( y - const );
( y - const );
 ( x - const ).
( x - const ).
Дифференцирование сложной функции.
Пусть функция z = f ( x , y ) – функция двух переменных, x и y, каждая из которых является функцией независимой переменной t,  В этом случае функция z = f ( x ( t ), y ( t )) является сложной функцией одной независимой переменной t; переменные x и y – промежуточные переменные.
В этом случае функция z = f ( x ( t ), y ( t )) является сложной функцией одной независимой переменной t; переменные x и y – промежуточные переменные.
Теорема:
Если z = f ( x , y ) – дифференцируемая в точке  функция и
функция и  и
и 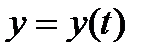 — дифференцируемые функции независимой переменной t, то производная сложной функции z=f(x(t),y(t)) вычисляется по формуле:
— дифференцируемые функции независимой переменной t, то производная сложной функции z=f(x(t),y(t)) вычисляется по формуле: 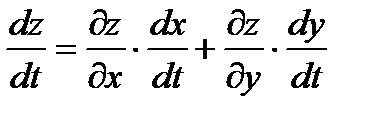
|
|
|
Доказательство:
Дадим независимой переменной t приращение  . Тогда функции
. Тогда функции  и
и 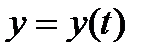 получат приращения
получат приращения 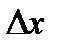 и
и 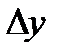 соответственно. В результате получим приращение функции
соответственно. В результате получим приращение функции 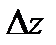 . Поскольку функция дифференцируема в точке
. Поскольку функция дифференцируема в точке  , то ее полное приращение можно записать в виде:
, то ее полное приращение можно записать в виде:  , где
, где  ,
, 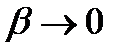 при
при 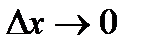 ,
,  . Разделим выражение
. Разделим выражение 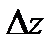 на
на  и перейдем к пределу при
и перейдем к пределу при 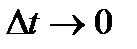 . Тогда
. Тогда 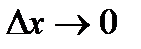 и
и  , в силу непрерывности функций
, в силу непрерывности функций  и
и 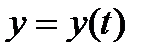 (по условию теоремы они – дифференцируемы, а следовательно - непрерывны).
(по условию теоремы они – дифференцируемы, а следовательно - непрерывны).
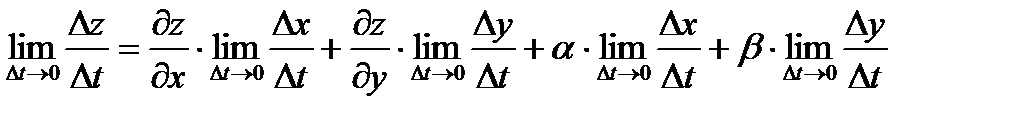 ,
,
то есть 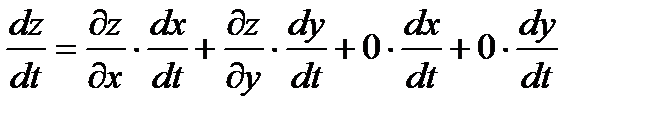 , или
, или 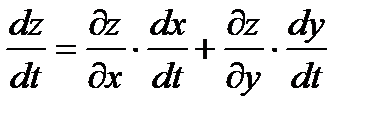 .
.
Частный случай: z = f ( x , y ), где y = y ( x ), то есть z = f ( x , y ( x )) – сложная функция одной независимой переменной x. Этот случай сводится к предыдущему, причем роль независимой переменной t выполняет x: 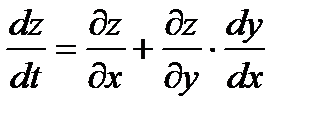 - формула полной производной.
- формула полной производной.
Общий случай: z = f ( x , y ), где x = x ( u , v ), y = y ( u , v ) то есть z = f ( x ( u , v ), y ( u , v )) – сложная функция независимых переменных u и v, частные производные которой находятся по формулам:
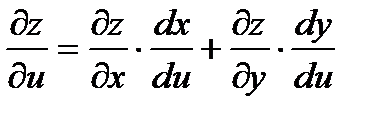
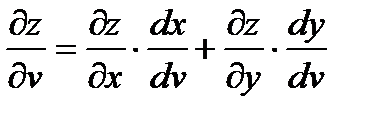
Таким образом, производная сложной функции z по каждой независимой переменной (u и v) равна сумме произведений частных производных этой функции по ее промежуточным переменным на их производные по соответствующей независимой переменной.
Пример:
Найти 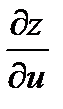 и
и 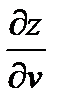 , если
, если  и
и 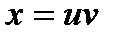 ,
, 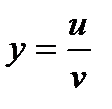 .
.
Решение:
|
|
|
Найдем 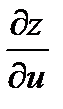 .
.
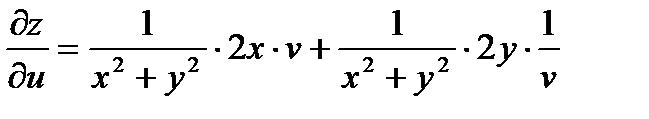 .
.
Упростим правую часть выражения:
 , то есть
, то есть
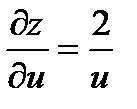
Найдем 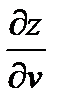 .
.
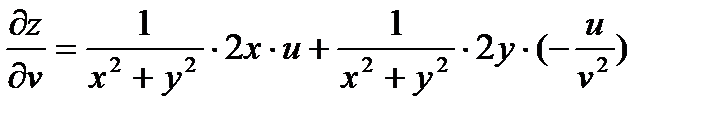
Упростим правую часть выражения:
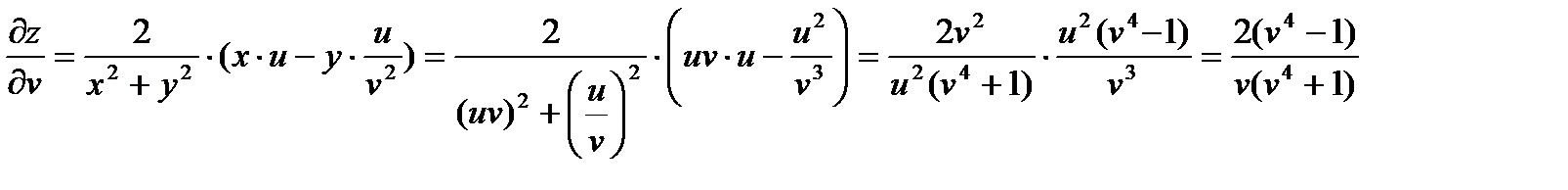 , то есть
, то есть  .
.
Дата добавления: 2019-09-13; просмотров: 271; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
