Геометрический смысл полного дифференциала функции двух переменных.
Напомним определение полного дифференциала:
Определение: Полным дифференциалом функции двух переменных называется главная часть полного приращения функции Dz=A×Dx+B×Dy+a линейная относительно Dx и Dy, где A и B – некоторые числа, а a-бесконечно малая, имеющая порядок малости выше, чем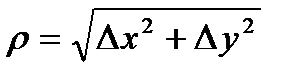 
(r-расстояние между точками) .
Таким образом, полный дифференциал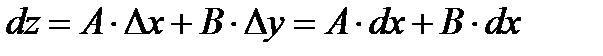 
.
Для случая двух переменных следует, что приращение функции f в окрестности некоторой точки М можно представить в виде
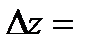
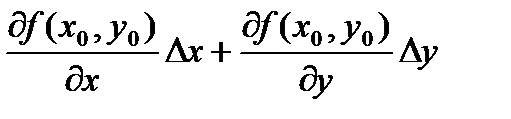
При этом дифференциал функции f имеет вид:
,
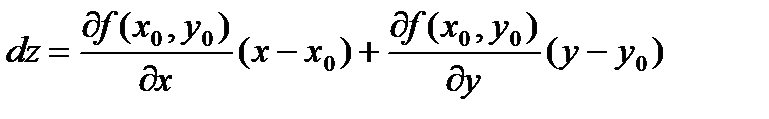что соответствует приращению аппликаты касательной плоскости к графику функции. В этом состоит геометрический смысл дифференциала.
Частные производные высших порядков.
Пусть функция двух переменных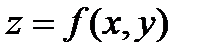 
имеет частные производные 
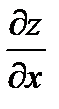и 
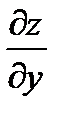, которые тоже зависят от двух переменных x и y Þ их тоже можно продифференцировать.
Определение: Частная производная от частных производных называются частными производными второго порядка.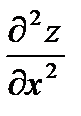 
, 
, 
. 
, 
, 
, 
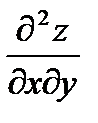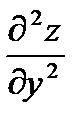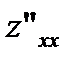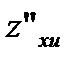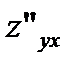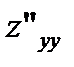
Аналогично можно ввести понятие частного производного 3, 4 и высших порядков.
Теорема:
Если функция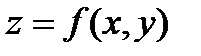 
непрерывна вместе с частным производным до второго порядка включительно, то смешанные производные второго порядка равны между собой 
.
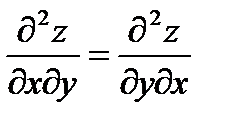Доказательство:
Рассмотрим выражение: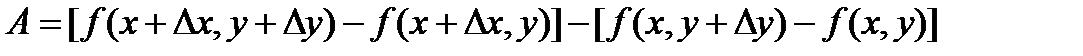 
Если ввести вспомогательную функцию: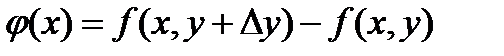 
, то можно A представить в виде: 
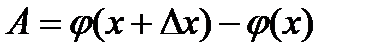. Поскольку 
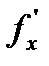определена в окрестности точки (x,y), следовательно, 
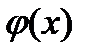дифференцируема на отрезке 
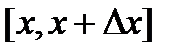. Тогда применяя теорему Лагранжа, получим: 
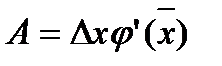, где 
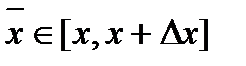. Но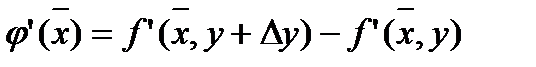 
. Поскольку 
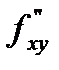определена в окрестности точки (x,y), то 
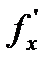дифференцируема на отрезке 
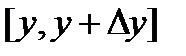. Применяя к разности теорему Лагранжа имеем:
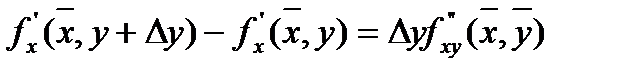, где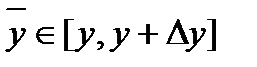 
.
Следовательно, первоначальное выражение имеет вид: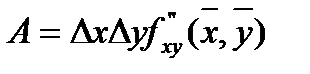 
.
Переставим слагаемые в первоначальном выражении:
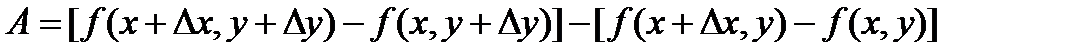и проведем аналогичные рассуждения. В результате получим: 
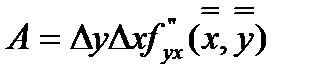, откуда следует 
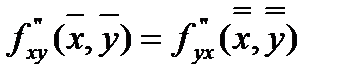. Переходя в этом равенстве к пределу и учитывая, что производные непрерывны в точке, окончательно получаем: .
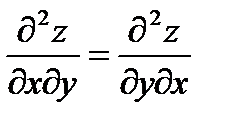Аналогичная теорема имеет место для функций большего числа переменных. Кроме того, данная теорема справедлива для производных порядка выше чем два.
Пример:
Найти все частные производные до 3 порядка включительно функции:
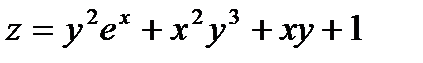
Решение:
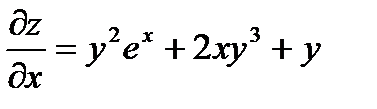
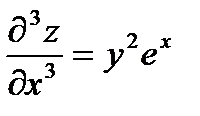
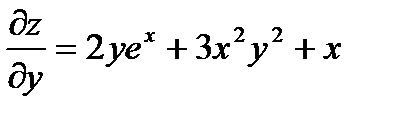
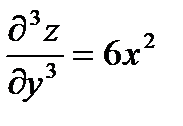
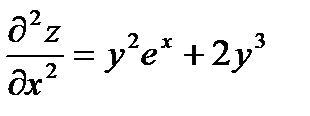
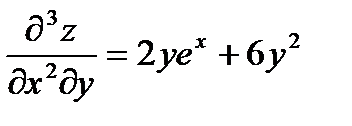
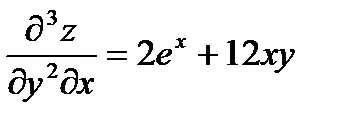
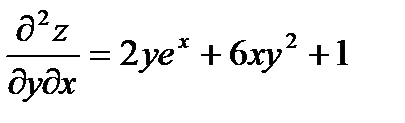
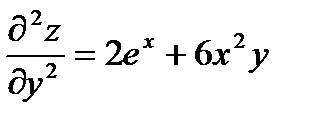
Формула Тейлора.
Пусть задана функция двух переменных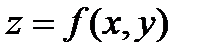 
, непрерывная вместе со своими частными производными до порядка n+1 в некоторой окрестности точки M(a,b). Тогда аналогично, как и для функции одной переменной функцию 2 переменных можно представить в виде суммы многочлена n-ого порядка по степеням (x-a) и (y-b) и некоторого остаточного члена.
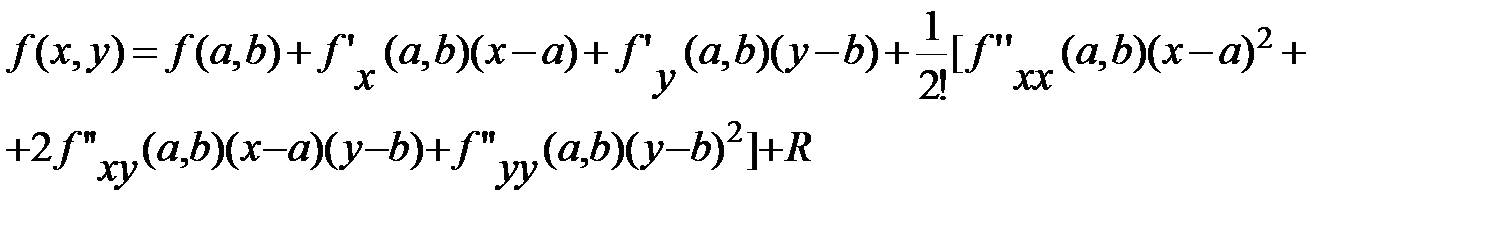
Это формула Тейлора для n=2, где R – остаток. Вид остатка в данной формуле аналогичен остатку в формуле Тейлора для функции одной переменной. При любом n формула имеет аналогичный вид.
Замечание: В дифференциальной форме формула Тейлора для случая нескольких переменных выглядит достаточно просто, однако в развернутом виде она весьма громоздка.
Дата добавления: 2019-09-13; просмотров: 378; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!