Координатный способ задания движения
Пример 1.1
Определить в интервале времени 
траекторию точки 
шатуна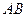 
кривошипно-шатунного механизма, если кривошип 
вращается вокруг шарнира 
так, что угол 
изменяется по закону 
где 
(Рис.1.1). Дано: 
Вычислим координаты точки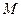 
для произвольного положения механизма.
Для исключения параметра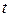 
воспользуемся основным тригонометрическим тождеством
Возводя каждое из уравнений движения в квадрат
и складывая полученные уравнения, находим:
|
| Рис.1.1 |
Таким образом, точка движется по эллипсу с полуосями 
и 
. При этом траекторией будет весь эллипс, поскольку он полностью укладывается в ограничения, получаемые из анализа кинематических уравнений движения: при 
имеем
Рассмотренный в этом примере кривошипно-шатунный механизм широко используется в технике для преобразования поступательного движения во вращательное и наоборот. Как видно, этот механизм можно также использовать в качестве чертежного инструмента для построения эллипсов с заданными полуосям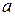и 
и 
. Достаточно подобрать величины 
и 
так, чтобы выполнялись условия
Отсюда 
Пример 1.2
Снаряд движется в вертикальной плоскости. Угол наклона ствола орудия к горизонту 
. Начальная скорость снаряда 
. Определить траекторию снаряда, высоту и дальность обстрела, максимальную дальность обстрела. Сопротивлением воздуха пренебречь.
|
|
|
Заметим, что по условию задачи единственной силой, действующей на снаряд во время полета, является сила тяжести, которая сообщает снаряду ускорение свободного падения. Выбирая начало координат в точке расположения орудия и направляя ось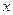 
горизонтально, а ось 
вертикально (Рис.1.2), находим:
или 
Получены обыкновенные дифференциальные уравнения первого порядка с разделяющимися переменными, интегрируя которые
находим при заданных начальных условиях
|
| Рис.1.2 |
законы изменения проекций скорости снаряда на координатные оси:
(a)
Уравнения (a) можно рассматривать как дифференциальные уравнения относительно координат снаряда.
Выполняя интегрирование
получаем закон движения снаряда:
(b)
Исключая время из уравнений (b) , получаем уравнение траектории снаряда:
|
|
|
представляющей собой часть параболы, расположенную над осью .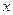
Обозначим 
время полета снаряда. Для момента падения снаряда имеем условия:
при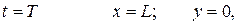 
где 
– дальность полета снаряда. Подставляя эти условия в уравнения (b) , получаем
Отсюда
Очевидно, дальность будет максимальной, когда 
принимает максимальное значение 
т.е.
при 
, т.е. при 
Для определения максимальной высоты 
снаряда воспользуемся тем, что в верхней точке траектории скорость горизонтальна. Обозначая 
время подъема снаряда на максимальную высоту, получаем
при 
.
Из уравнений (a) , (b) имеем:
Отсюда
Пример 1.3
Движение точки задано уравнениями
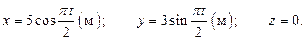
Найти траекторию точки в интервале времени и определить положение точки, ее скорость и ускорение в моменты времени 
и 
с.
Находим траекторию точки. Исключая параметр 
из уравнений движения, получаем
|
|
|
При имеем: 
Таким образом, траекторией является эллипс с полуосями 
м и 
м (Рис.1.3). Подставляя заданные моменты времени в уравнения движения точки, определяем ее координаты:
при 
при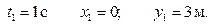 
Вычисляем скорость точки:
Подставляя в полученные формулы заданные моменты времени, находим:
при 
,
при 
Вычисляем ускорение точки:
|
| Рис.1.3 |
Подставляя в полученные формулы заданные моменты времени, находим:
при 
при 
Результаты изображены на Рис.1.3.
Подобным образом можно определить положение точки, ее скорость и ускорение в заданный момент времени при любых других заданных кинематических уравнениях движения точки в декартовой системе координат.
ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ:
Из сборника задач И.В.Мещерского: 10.2; 10.12; 10.14; 12.22; 12.23.
Из учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА - теория и практика»: комплект СР-16.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 2
Дата добавления: 2019-09-02; просмотров: 151; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!