Плоскопараллельное движение твердого тела. Задание движения

⇐ ПредыдущаяСтр 4 из 11Следующая ⇒

Движение тела называется плоскопараллельным, если расстояние от любой точки тела до некоторой неподвижной (основной) плоскости остается неизменным во все время движения

Проведем сечение тела параллельное основной плоскости (Рис. 2.6). Через любую точку сечения проведем отрезок , перпендикулярный основной плоскости. Из определения плоскопараллельного движения следует, что отрезок движется поступательно. Таким образом, движение сечения полностью определяет плоскопараллельное движение тела.

Рассмотрим движение сечения (плоской фигуры) в своей плоскости (Рис. 2.7). Пусть любая точка плоской фигуры. Примем точку за начало системы координат , оси которой движутся поступательно по отношению к основной системе . По отношению к системе плоская фигура может только вращаться вокруг подвижной оси .



Рис. 2.6		Рис. 2.7

Чтобы задать положение плоской фигуры, а следовательно, и всего тела, необходимо задать положение точки – полюса, а также задать вращение плоской фигуры по отношению к системе . Таким образом, закон плоскопараллельного движения тела имеет вид:

т.е. при плоскопараллельном движении тело имеет три степени свободы. Как видно, два первых уравнения описывают поступательную часть плоского движения, а последнее уравнение описывает вращение тела вокруг оси, проходящей через полюс .

Вычисление скорости любой точки тела. Вычислим скорость любой точки тела. В любой момент времени имеет место равенство (Рис. 2.7)

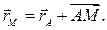
Тогда

(2.4)

Рис. 2.8

Вектор представляет собой скорость, полученную точкой при вращении плоской фигуры вокруг оси . Этот вектор направлен перпендикулярно отрезку 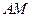(по касательной к окружности, которую описывает точка при вращении тела вокруг оси ), причем в сторону вращения тела (Рис. 2.8). Модуль скорости определяется по формуле Эйлера:

Поскольку вектор перпендикулярен отрезку 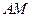, из формулы (6.4) получаем полезное для практических целей утверждение, которое обычно называют теоремой о проекциях:

проекции скоростей концов отрезка, соединяющего две точки абсолютно твердого тела, на направление этого отрезка равны.

Мгновенный центр скоростей. Как уже говорилось, за полюс можно принять любую точку плоской фигуры. В данный момент времени различные точки тела имеют разные скорости. За полюс имеет смысл принимать точку, скорость которой в данный момент времени равна нулю.

Рис. 2.9

Точка, принадлежащая плоской фигуре или неизменно с ней связанная, скорость которой в данный момент времени равна нулю, называется мгновенным центром скоростей.

Примем за полюс мгновенный центр скоростей 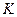. В соответствии с формулой (3.1), получаем, что скорость любой точки плоской фигуры определяется так же, как если бы тело вращалось вокруг оси 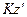(Рис. 2.9):

так как

Рассмотрим способы определения положения мгновенного центра скоростей.

1. Пусть известны направления скоростей двух точек и плоской фигуры, причем вектор не параллелен вектору . Как видно из Рис. 3.4, в этом случае мгновенный центр скоростей лежит в точке пересечения перпендикуляров, проведенных через точки и к векторам скоростей этих точек.


Рис. 2.10		Рис. 2.11

2. Пусть известны направления скоростей двух точек и , причем вектор параллелен вектору , но отрезок 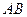не перпендикулярен скоростям (Рис. 2.10).

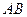Проекции скоростей точек и на направление , в соответствии с теоремой о проекциях, равны между собой и, следовательно, равны между собой векторы скоростей Используя формулу (3.1) , получаем

т.е. отсюда:

Таким образом, в данный момент времени угловая скорость тела равна нулю и скорости всех точек тела одинаковые. Имеем мгновенно поступательное распределение скоростей. Что касается положения мгновенного центра скоростей, то как видно из Рис. 6.11, перпендикуляры к скоростям оказываются параллельными. Можно считать, что мгновенный центр скоростей находится в бесконечно удаленной точке.

3. Пусть скорости точек и параллельны между собой и перпендикулярны отрезку 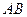(Рис. 2.11). В этом случае перпендикуляры к скоростям сливаются. Положение

Рис. 2.12

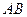мгновенного центра скоростей на перпендикуляре можно определить из соображений пропорциональности модулей скоростей расстояниям от точек до мгновенного центра скоростей. Расстояние можно определить из системы уравнений

которую удобнее всего решить графически. Заметим, что в рассматриваемом случае для определения положения мгновенного центра скоростей кроме направления скоростей двух точек необходимо знать и их модули.

4. Особый интерес представляет случай качения колеса по неподвижной поверхности. Если колесо катится без проскальзывания, то мгновенный центр скоростей находится в точке касания колеса и опорной поверхности (Рис. 2.12).

Вычисление ускорений точек тела, совершающего плоскопараллельное движение. Ускорение любой точки 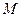плоской фигуры складывается из ускорения точки , принятой за полюс, и ускорения, полученного точкой 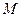при вращении плоской фигуры вокруг оси, проходящей через полюс перпендикулярно плоской фигуре:

Рис. 2.13

(2.5)

Вектор удобно разложить на составляющие – на вращательное и осестремительное ускорения (Рис. 2.13):

Уравнение (2.5) можно решать аналитически или геометрически. При аналитическом способе решения уравнение (2.5) записывают в проекциях на оси координат, одну из которых можно направить по прямой, соединяющей точки и 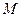, а вторую перпендикулярно :

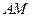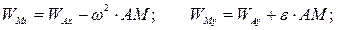
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ

1. Что называется плоскопараллельным движением твёрдого тела?

2. Из каких простейших движений складывается плоскопараллельное движение?

3. Как при плоскопараллельном движении связаны между собой скорости двух любых точек тела?

В чём состоит теорема о проекциях скоростей двух любых точек твёрдого тела?
Что называется мгновенным центром скоростей?

6. Как определяется положение мгновенного центра скоростей?

7. Как определить скорость точки при помощи мгновенного центра скоростей?

8. Как при плоскопараллельном движении связаны между собой ускорения двух любых точек тела?

ЛЕКЦИЯ 4 (8)

СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ

Основные определения

Часто возникает необходимость рассматривать движение точки одновременно по отношению к двум или более системам отсчета, движущимся относительно друг друга. В таком случае движение точки называется сложным.

Пусть система отсчета условно неподвижна, а система движется по отношению к неподвижной произвольным, но известным образом (Рис. 3.1).

Рис. 3.1

Движение точки 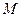по отношению к неподвижной системе отсчета называется абсолютным. Ее скорость и ускорение по отношению к неподвижной системе отсчета называются абсолютной скоростью и абсолютным ускорением .

Движение точки 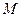по отношению к подвижной системе отсчета называется относительным. Скорость и ускорение точки по отношению к подвижной системе отсчета называются относительной скоростью 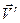и относительным ускорением .

Точки подвижного пространства совершают переносное для точки 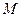движение. Различные точки подвижного пространства имеют в данный момент времени в общем случае разные скорости и разные ускорения.

Переносной скоростью 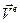и переносным ускорением точки 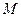называется скорость и ускорение той точки 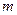подвижного пространства. в которой в данный момент времени находится движущаяся точка .

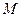Связи между абсолютными, относительными и переносными скоростями и ускорениями устанавливаются соответствующими теоремами, для доказательства которых нам понадобятся некоторые вспомогательные положения.

Дата добавления: 2019-09-02; просмотров: 354; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 345 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!